Ferromagnétisme

Le ferromagnétisme est le mécanisme fondamental par lequel certains matériaux (fer, cobalt, nickel…) sont attirés par des aimants ou forment des aimants permanents. On distingue en physique différents types de magnétismes. Le ferromagnétisme (qui inclut le ferrimagnétisme)[1] se trouve être celui à l’origine des champs magnétiques les plus importants : c’est celui qui crée des forces suffisamment importantes pour être senties et qui est responsable du phénomène bien connu de magnétisme dans les aimants de la vie quotidienne. La matière répond faiblement aux champs magnétiques selon trois autres types de magnétismes : le paramagnétisme, le diamagnétisme et l’antiferromagnétisme, mais les forces mises en jeu sont le plus souvent très faibles au point qu’elles ne peuvent être détectées que par des instruments de laboratoire particulièrement sensibles.
Le ferromagnétisme désigne la capacité de certains corps à s'aimanter sous l'effet d'un champ magnétique extérieur et à garder une partie de cette aimantation[2]. Ces corps sont soit de type ferromagnétique soit de type ferrimagnétique, de même que les matériaux qui se trouvent attirés par eux de façon significative. Ils se distinguent des paramagnétiques qui ne conservent pas leur aimantation à champ nul. Seules quelques substances se trouvent être ferromagnétiques. Les plus communes sont le fer, le nickel, le cobalt et la plupart de leurs alliages, certaines terres rares, et quelques minéraux naturels.
Il existe deux sous-catégories, à savoir les ferromagnétiques durs (que l'on appelle aimants permanents) et les ferromagnétiques doux. Ces matériaux se rencontrent dans l'industrie comme dans la vie quotidienne.
Le ferromagnétisme se trouve être très important pour l’industrie et les nouvelles technologies car il est à la base de nombreux appareils électriques et électrochimiques comme les électroaimants, les générateurs électriques, les transformateurs et les mémoires magnétiques (cassettes, disques durs, etc.).
Définitions[modifier | modifier le code]
Aimantation[modifier | modifier le code]
Un matériau magnétique est caractérisé par la présence de moments magnétiques. L'existence de ces moments est due au mouvement des électrons, dits de valence, dans les atomes. Ce sont des grandeurs vectorielles, qui ont donc une direction et qui ont pour unité des A m2.
Lorsqu'on considère la globalité du matériau, on peut définir une nouvelle grandeur : l'aimantation. Il s'agit de la somme de tous les vecteurs moment magnétiques, divisée par le volume de l'échantillon :
Si le matériau est soumis à un champ magnétique externe, les moments magnétiques vont interagir avec celui-ci. Ils peuvent, par exemple, s'aligner suivant le champ induit.
Aimantation spontanée[modifier | modifier le code]
Dans le cas des matériaux ferromagnétiques, il existe une aimantation naturelle, sans besoin d'appliquer un champ magnétique extérieur sur le matériau: c'est l'aimantation spontanée. Cette aimantation existe grâce à l'alignement des moments magnétiques dans le matériau : un ordre magnétique apparaît.
Cette propriété permet l'existence d'aimants permanents.
Ferromagnétisme et autres ordres magnétiques[modifier | modifier le code]
Il existe différents types d'ordres magnétiques sous champ magnétique extérieur nul. Outre le ferromagnétisme, il en existe d'autres types, qu'il faut bien distinguer :
Un matériau est ferromagnétique si tous ses moments magnétiques contribuent positivement à son aimantation. Ces moments sont alignés et ont une même direction.

Si une partie des moments magnétiques est alignée dans le sens opposé (ou anti-alignés), il se forme une aimantation résultante nette. Ce matériau est dit ferrimagnétique[3].
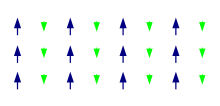
Si les moments alignés et anti-alignés se compensent complètement, ce qui produit une aimantation nette nulle, alors on dit que le matériau est antiferromagnétique.
Températures de Curie et de Néel[modifier | modifier le code]
Ces phénomènes d’alignement sont sensibles à la température, car l'agitation thermique peut altérer l'état des moments magnétiques. On parle particulièrement de températures seuils, au-dessus desquelles l'ordre magnétique disparaît :
- dans le cas des ferromagnétiques et ferrimagnétiques, on parle de température de Curie ;
- en ce qui concerne les antiferromagnétismes, on parle de température de Néel.

Au-delà de ces températures, l'ordre magnétique ne peut apparaître que sous champ magnétique externe : le matériau devient paramagnétique.
Histoire : distinction du ferri- et du ferromagnétisme[modifier | modifier le code]
Historiquement le terme ferromagnétisme était utilisé pour tous matériaux exhibant des propriétés d’aimantation, c’est-à-dire un moment magnétique net en l’absence de champ magnétique externe. Cette définition reste vulgairement utilisée. Cependant, plus récemment, différentes catégories d’aimantations spontanées ont été identifiées quand il y a plus d’un spin magnétique par maille du matériau, ce qui conduit à une définition plus stricte du « ferromagnétisme » qui la distingue du ferrimagnétisme. En particulier :
- un matériau est « ferromagnétique » au sens le plus strict si tous ses spins magnétiques contribuent positivement à une aimantation nette ;
- si une partie des spins se soustraient à l’aimantation nette (s'ils sont partiellement anti-alignés), alors le matériau est dit « ferrimagnétique »[3] ;
- si les moments des spins alignés et anti-alignés se compensent complètement, ce qui résulte en une aimantation nette de zéro malgré l’influence du champ magnétique, alors on dit que le matériau est antiferromagnétique.
Ces phénomènes d’alignement n’apparaissent qu’à des températures inférieures à une température seuil, dite température de Curie (pour les matériaux ferromagnétiques et ferrimagnétiques) ou température de Néel (pour les antiferromagnétiques).
Parmi les premières recherches sur le ferromagnétisme se trouvent les travaux pionniers d’Aleksandr Stoletov sur la détermination de la perméabilité magnétique des matériaux ferromagnétiques, connue sous le nom de courbe de Stoletov (en).
Matériaux ferromagnétiques[modifier | modifier le code]
Voir aussi la catégorie : materiaux ferromagnétiques.
Le tableau ci-dessous rassemble une sélection de matériaux ferromagnétiques et ferrimagnétiques associés à la température au-delà de laquelle ils cessent d’exhiber des propriétés d’aimantation spontanée (voir température de Curie).
| Matériaux | T° de Curie | Susceptibilité magnétique χm | ||
|---|---|---|---|---|
| K | °C | |||
| Co | 1 388 | 1 115 | 70 | |
| Fe α, aciers ferritiques et martensitiques | 1 043 | 770 | 200 | |
| MnBi | 630 | 357 | ||
| Ni | 627 | 354 | 110 | |
| MnSb | 587 | 314 | ||
| CrO2 | 386 | 113 | ||
| MnAs | 318 | 45 | ||
| Gd | 292 | 19 | ||
| Dy | 88 | -185 | ||
| EuO | 69 | -204 | ||
Le ferromagnétisme n’est pas seulement une propriété de l’arrangement chimique du matériau, mais aussi de sa structure cristalline et de sa micro-structuration. Il existe des alliages ferromagnétiques (dits alliages de Heusler) dont les composants ne sont pas eux-mêmes ferromagnétiques. A contrario, il existe des alliages non ferromagnétiques, tels que l’acier inoxydable austénitique, qui sont composés presque entièrement de métaux ferromagnétiques.
Des matériaux ferromagnétiques amorphes (non cristallins) peuvent être réalisés par une trempe (refroidissement) rapide d’un alliage sous forme liquide. Ceux-ci présentent l’avantage que leurs propriétés sont presque isotropes (non alignées selon les axes du cristal) ; cela résulte en une coercivité faible, des pertes d’hystérésis faibles, une haute permittivité et une haute résistivité électrique. Un matériau de ce type est un alliage métal de transition (80 % – souvent Fe, Co ou Ni) – métalloïde (20 % – B, C, Si, P ou Al) qui diminue le point de fusion.
Une catégorie relativement nouvelle de matériaux ferromagnétiques exceptionnellement forts sont les aimants terres-rares. Ils contiennent des éléments de la famille des lanthanides qui sont connus pour leur capacité à porter un grand moment magnétique sur leur orbitale f très localisée.
Ferro aimants à base d'actinides[modifier | modifier le code]
Un certain nombre d’actinides sont des ferro aimants à température ambiante ou présentent du ferromagnétisme si refroidis. PuP est un matériau paramagnétique à symétrie cubique à température ambiante, mais il subit une modification structurelle en symétrie tétragonale et devient ferromagnétique une fois refroidi sous Tc = 125 K.
Lithium (gaz)[modifier | modifier le code]
En 2009 une équipe de physiciens du MIT a démontré que le lithium (gaz) refroidi à une température inférieure à 1 K peut présenter du ferromagnétisme[4]. L’équipe a refroidi le lithium-6 fermionique à moins de 150 milliardièmes de kelvin au-dessus du zéro absolu en utilisant un procédé de refroidissement laser infrarouge.
Le ferromagnétisme à l'échelle macroscopique[modifier | modifier le code]
Un matériau ferromagnétique s’aimante sous l’effet d’un champ extérieur. Il convient donc d’étudier la susceptibilité d’un tel matériau.
Rappel de la définition de la susceptibilité[modifier | modifier le code]
Cette grandeur traduit la capacité d’un matériau à s’aimanter sous l’effet d’une excitation magnétique extérieure.
Dans le cas général, la susceptibilité vaut :
La susceptibilité des ferromagnétiques[modifier | modifier le code]
La susceptibilité χ des ferromagnétiques est positive et très grande. Sa valeur se situe entre 50 et 10 000. Dans le cas des ferromagnétiques doux, cette propriété est très utilisée car elle va permettre d'obtenir une forte induction à partir d'une faible excitation extérieure. C’est pour cela qu’on utilise ces derniers pour canaliser les lignes de champ. Les ferromagnétiques en général possèdent une aimantation spontanée et leurs propriétés dépendent de l’histoire magnétique du matériau, ce qui mène à l’étude des cycles d’hystérésis.
Le ferromagnétisme à l'échelle microscopique[modifier | modifier le code]
Le théorème de Bohr-van Leeuwen, découvert dans les années 1910, démontrait que les théories de physique classique sont incapables d’intégrer et d’expliquer le magnétisme, y compris le ferromagnétisme. Le magnétisme est à présent compris comme un phénomène purement quantique. Le ferromagnétisme est dû à deux effets de mécanique quantique : la théorie de spin et le principe d’exclusion de Pauli.
Origine du magnétisme[modifier | modifier le code]
L’une des propriétés fondamentales d’un électron (à part le fait qu’il porte une charge) est qu’il possède un moment dipolaire magnétique (i.e. il se comporte comme un petit aimant). Ce moment dipolaire vient d’une propriété plus fondamentale de l’électron et qui dit qu’il possède un spin quantique. De par sa nature quantique le spin ne peut se trouver que dans deux états « up » ou « down » selon l’orientation du champ magnétique. Le spin des électrons dans les atomes est la source principale de ferromagnétisme, bien qu’il y ait aussi une contribution du moment angulaire orbital de l’électron par rapport au noyau. Quand les dipôles magnétiques s’alignent dans un morceau de matière, leurs champs magnétiques individuels s’ajoutent pour créer un champ bien plus grand et perceptible à l’échelle macroscopique.
Cependant il est nécessaire que les atomes mis en jeu aient leur couche électronique partiellement remplie. En effet les atomes ayant leurs couches électroniques entièrement remplies ont un moment dipolaire total de zéro car tous les électrons existent en paires de spins opposés et le moment magnétique de chaque électron se retrouve compensé par le moment du second électron de la paire. A contrario un moment magnétique net (et donc du ferromagnétisme) peut apparaitre dans les matériaux dont les atomes possèdent des couches électroniques partiellement remplies (i.e. dont les électrons ont des spins non appariés). De plus à cause de la règle de Hund les premiers électrons d’une couche ont tendance à avoir le même spin, ce qui tend à augmenter le moment dipolaire total.
Ces dipôles non appariés ont tendance à s’aligner parallèlement au champ magnétique externe qu’on leur impose selon un effet que l’on appelle paramagnétisme. Le ferromagnétisme implique un phénomène supplémentaire : dans quelques substances les dipôles ont tendance à s’aligner spontanément en donnant lieu à une aimantation spontanée du milieu même alors qu’il n’y a pas eu de champ appliqué.
Il existe donc à l'échelle microscopique un ordre expliquant le ferromagnétisme. Pour le comprendre avec précision, il est nécessaire d'étudier l'interaction d'échange d'Heisenberg.
Interaction d’échange d'Heisenberg[modifier | modifier le code]
L'interaction d’échange d'Heisenberg est une interaction couplant deux spins consécutifs formant l’angle θi,j :
Cette interaction décroit très rapidement avec la distance. Elle met donc en jeu très majoritairement les premiers voisins.
- Pour , l’interaction d’échange tend à aligner les moments parallèlement entre eux. Il existe donc un moment magnétique macroscopique. L’ordre est dit ferromagnétique.
- Pour , les premiers voisins s’alignent antiparallèlement. Il n’y a donc pas de moment macroscopique résultant, sauf si les deux spins n'ont pas la même amplitude. L’ordre est dit antiferromagnétique.
Théorie du champ moléculaire[modifier | modifier le code]
Un matériau ferromagnétique présente une aimantation spontanée en dessous d’une température critique appelée température de Curie (Tc), et ce en l’absence de champ magnétique extérieur. Ce phénomène peut être décrit à l’aide de la théorie du champ moléculaire. La théorie du champ moléculaire permet notamment d'obtenir une expression pour l'aimantation spontanée d'un ferromagnétique.
Cette théorie décrit l'influence des voisins d'un atome dans la formation d'un champ magnétique proportionnel à l'aimantation. Ce champ existe en présence, ou pas, d'un champ magnétique extérieur. Ceci se traduit par :
La constante de Weiss α, aussi notée NW, représente la proportionnalité entre aimantation spontanée et le champ moléculaire.
On peut appliquer cette théorie sur les atomes par le modèle classique (fonction de Langevin) ou le modèle quantique (fonction de Brillouin) (voir article sur le paramagnétisme). Par la suite, la théorie du champ moléculaire sera appliquée sur les atomes du modèle quantique.
Dans le modèle quantique, on peut écrire :
La variable x s'écrit :
L’aimantation spontanée apparaît pour Happl=0. On peut donc écrire car .

On retrouve souvent la notation msp, pour l'aimantation spontanée réduite. On écrit:
De plus avec N le nombre de sites magnétiques par unité de volume. Il est possible de réécrire le terme dans la parenthèse pour obtenir :
L'aimantation msp se trouve dans le terme gauche, et dans le terme entre parenthèses. Cette équation peut être résolue graphiquement, en traçant les deux courbes :
- ;
- .

Lorsque la température T tend vers 0, msp tend alors vers 1 et donc Msp=Ms. De plus, lorsque T augmente on peut noter que msp diminue. Enfin, lorsque la pente est trop grande, il n’y a plus de solution à l’équation, et donc pas d’aimantation spontanée. La température de Curie (Tc) est la température pour laquelle apparaît ou disparaît msp . Elle correspond au moment où la pente BJ à l’origine vaut .
Sachant que lorsque x tend vers 0, Tc vérifie soit :
- .
Tc donne une mesure de l’importance des interactions d’échange.
En utilisant la même théorie, on peut calculer l’évolution de Msp avec Happl. Si l’on réussit à obtenir que l'approximation de ce champ est de faible intensité, il est alors possible de montrer que la susceptibilité χ s'écrit avec C la constante de Curie. Traditionnellement, pour représenter les propriétés magnétiques d’un matériau ferromagnétique, les courbes Ms(T) et sont tracées sur un même graphe.
Anisotropie magnétique[modifier | modifier le code]
Bien que l’interaction d’échange conserve l’alignement des spins, elle ne les aligne pas particulièrement dans une direction spécifique. Sans anisotropie magnétique, les spins d’un aimant changent de direction aléatoirement en réponse aux fluctuations thermiques et l’aimant est qualifié de superparamagnétique. Il y a plusieurs types d’anisotropie magnétique, la plus commune étant l’anisotropie magnétique cristalline : une dépendance de l’énergie de la direction de magnétisation en fonction de l’orientation du réseau cristallin. Une autre source commune d’anisotropie est l’effet magnétorestrictif inverse, induit par une contrainte mécanique interne. Les aimants uniformes sur un domaine peuvent aussi avoir une anisotropie de forme due aux effets magnétostatiques de la forme de la particule. Alors que la température de l’aimant augmente, l’anisotropie a tendance à diminuer et il existe souvent une température seuil à partir de laquelle une transition vers le superparamagnétisme a lieu[5].
L’anisotropie magnéto-cristalline[modifier | modifier le code]
Lorsque l’atome se trouve au sein d’un cristal, la présence des ions du réseau cristallin modifie les orbitales électroniques, elles subissent une levée de dégénérescence. Par exemple les orbitales 3d ne sont plus toutes équivalentes : celles dont la forme minimise l’énergie électrostatique due à la présence des ions voisins sont favorisées énergétiquement. Plus généralement, cela conduit à minimiser l'énergie lorsque le moment orbital pointe dans certaines directions du réseau cristallin par rapport à d’autres. Par suite, la présence du couplage spin-orbite conduit à favoriser énergétiquement certaines directions du moment magnétique total par rapport à d’autres.
Exemple : Pour le fer (Fe) les axes de facile aimantation sont : [001], [010] et [100].
L’anisotropie de forme[modifier | modifier le code]
Lorsqu’un matériau subit un champ magnétique externe, il se créé en son sein un champ démagnétisant dans une direction opposée. La présence de ce champ démagnétisant rend anisotropes les propriétés magnétiques du matériau selon sa forme (les propriétés magnétiques restent isotropes dans le cas d’une sphère). On retient que l’anisotropie de forme est indépendante de l’anisotropie magnéto-cristalline et tend à favoriser l’aimantation du matériau selon ses grandes dimensions.
L’anisotropie de surface[modifier | modifier le code]
Les atomes se trouvant à la surface du matériau ont un environnement différent de ceux se situant à l’intérieur. En effet le nombre d’atomes voisins est diminué de manière conséquente. Cela se traduit par l’apparition d’un terme d’énergie supplémentaire uniquement lié à la surface et favorisant l’orientation de l’aimantation perpendiculairement à cette dernière.
En conclusion, l’anisotropie magnétique tend à créer des axes de facile aimantation. Si un champ magnétique extérieur est appliqué selon ces axes, il sera plus facile de l’aimanter.
Les domaines magnétiques[modifier | modifier le code]

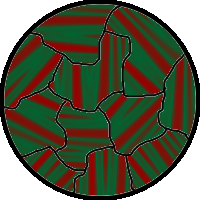
Le paragraphe précédent semble suggérer que chaque morceau de matériau ferromagnétique devrait avoir un champ magnétique intense, étant donné que tous les spins sont alignés. Pourtant il se trouve que le fer et la plupart des autres ferro aimants sont souvent trouvés dans un état « non aimanté ». Cela s’explique par le fait que le matériau ferromagnétique est divisé en de nombreuses petites régions appelées domaines magnétiques (aussi connus sous le nom de domaines de Weiss), la paroi séparant plusieurs domaines est appelée « paroi de Bloch ». À l’intérieur de chacun de ces domaines les spins sont alignés, mais les spins de domaines différents pointent dans des directions variées et leurs champs magnétiques se compensent. L’objet n’a alors pas de champ magnétique apparent pour l’observateur.

Les matériaux ferromagnétiques se divisent spontanément en domaines magnétiques car leur interaction d’échange est une force à courte portée, c’est pourquoi sur de longues portées la tendance des dipôles à réduire leur énergies en s’orientant en des directions opposées prend le dessus. Les domaines sont séparés par de fines parois de domaines, épaisses de quelques molécules dans lesquelles la direction d’aimantation du dipôle tourne doucement d’une direction de domaine à l’autre.
Les cycles d’hystérésis[modifier | modifier le code]
Définition[modifier | modifier le code]
Lorsque l'on applique un champ magnétique externe sur un matériau ferromagnétique, les moments magnétiques s'orientent dans la même direction que le champ. Par la suite, même lorsque le champ est supprimé, une partie de l'alignement est conservée : le matériau s'est aimanté. En appliquant un champ magnétique opposé suffisamment intense, les moments magnétiques se renversent mais l'aimantation ne suit pas le chemin initial. Il y a un cycle d'hystérésis.
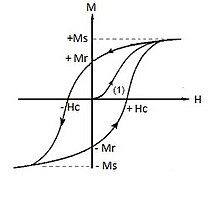
En partant d'un matériau désaimanté (H = M = 0), le tracé de la variation de M en fonction de H avec l'augmentation de l'intensité du champ, M suit la courbe dite de première aimantation.
Cette courbe augmente rapidement au début, puis se rapproche d'une asymptote appelée « saturation magnétique ». Si le champ magnétique est maintenant réduit de façon monotone, M suit une courbe différente. À champ nul, l'aimantation est décalée par rapport à l'origine d'une quantité appelée la rémanence. La diminution supplémentaire du champ conduit à la diminution progressive de l'aimantation, et passe par zéro au moment du champ coercitif. À partir de là, l’aimantation s'inverse puis arrive à un minimum obtenu pour des valeurs de champ négatives. Le tracé de toutes les valeurs de l'aimantation en fonction du champ magnétique montre une courbe d'hystérésis.
Grandeurs notables[modifier | modifier le code]
- l’aimantation à saturation Ms correspond à l'aimantation maximale du matériau ;
- l’aimantation rémanente Mr est l’aimantation sans excitation extérieure ;
- le champ coercitif est le champ pour lequel l’aimantation est nulle.
Les ferromagnétiques durs[modifier | modifier le code]
Ces matériaux ont une aimantation rémanente et un champ coercitif élevés. Ils sont utilisés pour fabriquer les aimants permanents.
Les ferromagnétiques doux[modifier | modifier le code]
Ils ont un champ coercitif très faible et une très forte susceptibilité. Le cycle est donc très étroit.
L’aire représentée à l'intérieur du cycle correspond aux pertes magnétiques lorsque le matériau effectue un cycle complet. Cette perte magnétique se traduit en émission de chaleur. Ces émissions de chaleur sont problématiques pour un grand nombre d'applications. On comprend donc que ces matériaux sont utilisés pour des applications travaillant en fréquence car leur cycle est étroit et donc les pertes sont minimisées.
Courbe de première aimantation[modifier | modifier le code]

Les domaines magnétiques ne sont pas physiquement contraints et fixés et peuvent être modifiés par l’application d’un champ magnétique extérieur. À partir d’une aimantation nulle à champ nul, en augmentant faiblement le champ extérieur, des moments magnétiques dans certains domaines se retournent. Si un domaine est déjà aligné dans le sens du champ appliqué, les domaines voisins s’alignent progressivement. Cela revient à un déplacement de la paroi de Bloch. Ce mécanisme, réversible pour de faibles champs, devient irréversible pour des champs extérieurs moyens. Enfin, pour de fortes excitations magnétiques, il se produit une rotation des aimantations des domaines dans la direction du champ extérieur. Macroscopiquement, Ms est atteinte.
Ceci correspond à la courbe de première aimantation jusqu’à saturation.
Les domaines resteront alignés même après l’extinction du champ externe car les parois de domaine ont tendance à rester « coincées » ou « bloquées » sur des défauts du réseau cristallin. Cela est montré par l’effet Barkhausen : alors que le champ d’aimantation est changé, l’aimantation change par des centaines de petits sauts discontinus alors que les parois de domaines passent les défauts cristallins.
L’aimantation en fonction du champ externe est décrite par une courbe d’hystérésis. Bien que cet état de domaines alignés décrit précédemment ne soit pas d’énergie minimale, il est métastable et peu perdurer sur de longues périodes.
Chauffer puis refroidir (annealing) un matériau, le soumettre à des vibrations en le martelant tendent à relâcher les parois de domaine de leur position « bloqué » et les limites des domaines ont tendance à se replacer de façon à minimiser l’énergie. On a alors démagnétisé le matériau.
Origine de l’hystérésis[modifier | modifier le code]
En faisant décroître l’excitation magnétique H, la courbe de désaimantation ne prend pas le chemin initial et passe au-dessus de la courbe d’aimantation. Ce retard à la désaimantation est dû à l’irréversibilité du déplacement des parois de Bloch.
Influence de la température[modifier | modifier le code]

La température influence fortement l’ordre magnétique établi. On définit la température de Curie Tc comme étant la température critique au-delà de laquelle le matériau n'est plus ferromagnétique mais paramagnétique.
Pour T<Tc, il existe un ordre magnétique dû en partie à l’interaction d’échange Heisenberg. Le matériau est ferromagnétique.
Pour T>Tc, l’agitation thermique est telle qu’il n’existe plus d’ordre. Le matériau se comporte alors comme un paramagnétique.
Alors que la température augmente, l’agitation thermique (ou entropie) rivalise avec les tendances ferromagnétiques des dipôles à s’aligner. Quand la température dépasse un certain seuil, appelé température de Curie, il se passe une transition de phase du second ordre et le système ne peut plus maintenir sa magnétisation spontanée et sa capacité à être aimanté ou à attirer des aimants disparait bien qu’il soit toujours paramagnétique pour un champ extérieur. En dessous de cette température il y a une rupture de symétrie spontanée et les moments magnétiques s’alignent avec leurs voisins. La température de Curie est un point critique où la susceptibilité magnétique se trouve être théoriquement infinie.
Notes et références[modifier | modifier le code]
- Chikazumi 2009, p. 118
- « Ferromagnétique », sur futura-sciences.com, Futura-Sciences (consulté le ).
- (en) Herrera, J. M.; Bachschmidt, A; Villain, F; Bleuzen, A; Marvaud, V; Wernsdorfer, W; Verdaguer, m, « Mixed valency and magnetism in cyanometallates and Prussian blue analogues », Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, , p. 127-138
- (en) G-B Jo; Y-R Lee; J-H Choi; C. A. Christensen; T. H. Kim; J. H. Thywissen; D. E. Pritchard; W. Ketterle, « "Itinerant Ferromagnetism in a Fermi Gas of Ultracold Atoms" », Science, , p. 1521-1524
- (en) Aharoni, Amikam, Introduction to the Theory or Ferromagnetism, Oxford, Clerendon Press, , 315 p. (ISBN 0-19-851791-2)
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Max Brousseau, Physique du solide. Propriétés électroniques, Paris, Masson, 1992 (ISBN 2-225-83975-1).
- José-Philippe Pérez, Robert Carles et Robert Fleckinger, Électromagnétisme fondements et applications, Liège, Dunod, 2001 (ISBN 2-10-005574-7).
- José-Philippe Pérez, Robert Carles et Robert Fleckinger, Électromagnétisme Vide et milieux matériels, Paris, Masson, 1990 (ISBN 2-225-82294-8).
- François Leprince-Ringuet, « Matériaux ferromagnétiques usuels », Techniques de l'ingénieur, 1994.
- Jean-Pierre Nozière, « Ferromagnétisme », Techniques de l'ingénieur, 1998.
- Jean-Louis Porteseil, « Ferromagnétisme », Techniques de l'ingénieur, 1989.
- (en) Soshin Chikazumi, Physics of ferromagnetism, Oxford : Oxford University Press, , 655 p. (ISBN 978-0-19-956481-1, lire en ligne), p.118
Articles connexes[modifier | modifier le code]
- Matériau ferromagnétique dur
- Matériau ferromagnétique doux
- Magnétisme
- Diamagnétisme
- Pôle magnétique
- Modèle de Stoner-Wohlfarth, critère de Stoner
























