Dislocation (matériaux)
En science des matériaux, une dislocation est un défaut cristallin linéaire[Note 1], correspondant à une discontinuité dans l'organisation de la structure cristalline. Une dislocation peut être vue simplement comme un "quantum" de déformation élémentaire au sein d'un cristal possédant un champ de contrainte à longue distance.
Elle est caractérisée par la direction de sa ligne et par son « vecteur de Burgers » (qui décrit la déformation qu'elle engendre).
Les dislocations ont une importance capitale pour les propriétés physiques des matériaux cristallins. Notamment, elles permettent leur déformation plastique (ductilité), facilitent la diffusion des atomes et influencent les propriétés électroniques des semi-conducteurs.
La dynamique des dislocations est la simulation numérique du mouvement des dislocations à une échelle micrométrique.
Histoire d'un concept[modifier | modifier le code]
Le paradoxe de la déformation[modifier | modifier le code]
Il est clair que la déformation plastique nécessite un réarrangement important de la matière. Pourtant cette situation semble paradoxale dans les métaux, où la structure interne (celle d’un cristal où les atomes sont répartis sur un réseau périodique tridimensionnel) doit être conservée malgré les changements de forme extérieure. La façon la plus intuitive d’imaginer la déformation est de considérer qu’elle procède par une série de glissements élémentaires le long de plans atomiques, à la manière des feuilles d’une rame de papier qui glissent les unes sur les autres. Ceci est appelé un cisaillement. Les métallurgistes du début du siècle avaient compris que la déformation s’effectuait par de tels « glissements ». Ils avaient remarqué en particulier que les cristaux fragiles se brisaient le long de certains plans en formant des facettes bien particulières, appelées surfaces de clivage, et que l’on observe si facilement dans les minéraux (quartz, diamant…).

Lorsque l’on déforme un cristal, on peut observer dans certaines conditions de petites marches sur leurs surfaces. Il est facile de comprendre que lorsqu’on fait glisser un plan d’atomes l’un sur l’autre (on parle d’un plan de glissement), on crée un décalage qui forme une marche en surface. Dans ce processus, la structure du cristal reste préservée si le cisaillement est un multiple de la période du réseau cristallin.
Si on calcule la contrainte nécessaire pour cisailler un cristal parfait (sans défauts), on s'aperçoit qu'elle serait de 1000 à 10 000 fois la contrainte réelle observée. Si un tel cristal parfait existait, on pourrait suspendre une voiture à un fil d'acier de 1 mm de diamètre.
L'énigme expliquée[modifier | modifier le code]
Dans les années 1930, Orowan, Polanyi et Taylor proposèrent que le cisaillement pouvait se produire par la propagation de défauts linéaires élémentaires appelés dislocations[1].

Supposons qu’un cisaillement élémentaire d’une distance inter-atomique b se produise uniquement le long d’une partie du plan de cisaillement. La ligne qui sépare la partie qui a été cisaillée de celle qui ne l’est pas, est la ligne de dislocation. Elle apparaît ici comme la limite d’un demi plan atomique qui distord fortement les plans voisins.
Bien qu'observées dans les cristaux liquides au début du XXe siècle par Georges Friedel, il aura fallu attendre les années 1950 et l'invention du microscope électronique en transmission pour les observer dans les métaux.
Dislocations modèles[modifier | modifier le code]

Le concept de dislocation dans un milieu « continu » est bien connu depuis les travaux du mathématicien Volterra au début du XXe siècle. La construction dite « de Volterra » permet de créer formellement une dislocation. Elle consiste[2] :
- dans un premier temps à couper un volume selon une surface quelconque s'appuyant sur une ligne ;
- puis à déplacer l'une des lèvres de coupure par rapport à l'autre selon un vecteur (appelé « vecteur de Burgers ») ; dans les solides cristallins (un milieu discontinu), ce vecteur est toujours une translation du réseau ;
- enfin, dans une dernière étape, il s'agit de recoller les deux lèvres de la coupure et de relaxer les contraintes nécessaires au déplacement.
Lorsque ce déplacement est en dehors du plan de coupe, le recollement nécessite l'ajout de matière.
Cette construction aboutit à la formation d'une discontinuité linéaire (purement élastique dans un milieu continu) bordant la surface. La dislocation ainsi créée est définie par la position géométrique de la ligne et de la force nécessaire au déplacement relatif des deux lèvres. Elle ne dépend pas de la position de la surface de coupure. Dans un milieu discontinu, la ligne marque le « cœur » de la dislocation. Dans cette région, le déplacement des atomes de leur position initiale ne peut pas être défini par une déformation élastique.
La ligne de dislocation ne peut s'arrêter à l'intérieur du cristal mais doit soit émerger sur une imperfection (surface, joint de grain, autre dislocation) soit se refermer sur elle-même. Deux cas particuliers de dislocations rectilignes sont intéressants : la dislocation coin ( perpendiculaire à , vecteur unitaire de la ligne ) et la dislocation vis ( parallèle à ).
Dislocation coin[modifier | modifier le code]
Elle peut être visualisée aisément si on effectue le processus de Volterra en insérant un demi-plan atomique supplémentaire dans la structure parfaite, à la manière dont on enfoncerait un coin dans une pièce de bois[3].
Ce mode d'adaptation est utilisé par certaines plantes lorsque des lignes parallèles suivent une forme de largeur variable, comme les lignes de grains sur un épi de maïs ou les lignes d'aiguilles sur un cactus.
Dans une dislocation coin, la force est perpendiculaire à la dislocation.
Dislocation vis[modifier | modifier le code]
La dislocation vis tire son nom du fait que chaque point sur le « plan » atomique perpendiculaire à la ligne de dislocation monte d’un pas égal à à chaque tour d’une trajectoire qui enroule la dislocation. La topologie du champ de contrainte autour de la dislocation est donc celle d’une hélice, ou encore, si on fait le tour de la ligne en sautant d'atome en atome, on monte de lorsque l'on fait un tour[4].
Dislocation réelle[modifier | modifier le code]
Dans le cas général, la dislocation a un caractère dit mixte, où le vecteur de Burgers et le vecteur unitaire de la ligne forment un angle quelconque.
La ligne de dislocation est de manière générale courbe, la dislocation présente de fait des portions à caractère mixte.
Mouvement des dislocations[modifier | modifier le code]
Il existe deux types de mouvement :
- le glissement, correspondant au mouvement de la dislocation dans le plan (en jaune sur le schéma ci-contre) défini par son vecteur de Burgers et la direction de sa ligne
- la montée correspondant au mouvement en dehors du plan de glissement.
Le glissement[modifier | modifier le code]
Ce mouvement est dit « conservatif » car il ne nécessite pas de transport de matière. Il s'effectue de proche en proche par la rupture et le recollement des liaisons atomiques à la manière dont on ferait glisser une double fermeture éclair. Ce type de mouvement est particulièrement efficace pour propager la déformation, et se produit généralement sans autre apport énergétique qu'une faible contrainte extérieure. De façon imagée, on s'imagine très bien qu'il est plus facile de traîner un tapis sur le sol en faisant propager une série de petites bosses plutôt que de tirer l'ensemble du tapis.
- Force de Peierls
C'est une force de frottement du réseau, elle s'oppose au glissement des dislocations, elle a été découverte par Rudolf Peierls et modifiée par Frank Nabarro d'où le PN en indice, son amplitude varie périodiquement en fonction du déplacement de la dislocation dans le plan[5],[6]. Elle est donnée par la loi :
- tel que :
- = c'est le module de cisaillement
- = coefficient de Poisson
- = espacement interatomique
- = espacement inter-planaire
Elle dépend de plusieurs critères :
- la taille d'une dislocation et sa largeur,
- la distance entre les plans,
- la température.
La force de Peierls a une valeur élevée quand les liaisons sont orientées (c'est-à-dire polarisées par exemple : les liaisons hydrogène) comme dans les cristaux covalents et une valeur relativement faible pour les métaux, et elle atteint le minimum dans les plans compacts.
La montée[modifier | modifier le code]
Pour déplacer une dislocation en dehors de son plan de glissement, il est nécessaire de déplacer des atomes sur de longues distances : le processus est non conservatif et a lieu grâce à la diffusion des lacunes ou d'atomes interstitiels dans le matériau vers le cœur de la dislocation. Comme la quantité des lacunes/interstitiels et leur diffusion est un processus thermiquement actif, la montée apparaît généralement à haute température[7].
Propriétés des dislocations[modifier | modifier le code]
Vecteur de Burgers[modifier | modifier le code]
Le vecteur de Burgers se définit comme étant le vecteur nécessaire à boucler un circuit initialement fermé dans le cristal parfait et qui se trouve ouvert lorsqu'il enlace la ligne de dislocation. Ce vecteur n'est pas quelconque dans un cristal mais représente une translation du réseau[8]. Par exemple dans l'aluminium cubique faces centrées, le vecteur de Burgers traditionnellement rencontré est b= a/2 [110], de norme |b|= 0.29 nm. En termes plus mathématiques[9], il s'agit de l'intégrale du déplacement sur un circuit fermé C enlaçant la ligne de dislocation u :
Physiquement, le vecteur de Burgers représente l'amplitude de la déformation transportée par une dislocation. Comme les dislocations sont des objets flexibles, deux dislocations peuvent interagir pour former une troisième dislocation si et seulement si la quantité de déformation est conservée : on parle de jonction attractive. Il s'ensuit qu'à un nœud entre plusieurs dislocations, la somme des vecteurs de Burgers est nulle (analogue de la loi des nœuds de Kirchhoff).
Champ de contrainte élastique[modifier | modifier le code]
Comme une dislocation isolée est une singularité élastique, elle développe un champ de contrainte à longue distance, de la même façon qu'un électron est entouré d'un champ électromagnétique de portée infinie. Dans le cas d'une dislocation vis, il est de la forme[10] : (il s'agit en réalité d'un tenseur dont les seules composantes non nulles correspondent à des cisaillements purs dans les plans radiaux parallèles à u et dans les plans horizontaux perpendiculaires à un rayon autour de la dislocation)
On voit qu’il est proportionnel au vecteur de Burgers (ce qui est analogue à la charge électrique), au module de cisaillement (analogue à la permittivité électrique du milieu), et inversement proportionnel à la distance. Ainsi, une dislocation peut être vue comme un quantum de déformation élémentaire.
Interaction avec une contrainte extérieure[modifier | modifier le code]
Comme les dislocations possèdent un champ élastique, elles peuvent interagir avec un champ extérieur.
Interaction avec une autre dislocation[modifier | modifier le code]
Interaction avec le réseau[modifier | modifier le code]
Le réseau cristallin étant périodique, il y a des positions où la dislocation a une énergie élastique plus importante que d'autres. Le déplacement de la dislocation nécessite de vaincre ces « barrières énergétiques » ; on a donc un phénomène similaire au frottement. Cette force de frottement induite est appelée « force de Peierls-Nabarro ».
De fait, lorsqu'un métal subit une déformation plastique, il s'échauffe.
Interaction avec des défauts ponctuels[modifier | modifier le code]
Les dislocations attirent les atomes ne faisant pas partie du réseau (atomes étrangers : impuretés ou éléments d'alliage). Si ces atomes étrangers sont mobiles, ils migrent vers les dislocations et constituent un « nuage de Cottrell ». Ce nuage de Cottrell gêne le mouvement des dislocations. Lorsque la force de déformation (la contrainte) est suffisante pour arracher la dislocation à son nuage, la mobilité augmente subitement ; ceci explique le décrochement observé parfois sur les courbes de traction.
Si les atomes sont mobiles (température suffisante pour permettre la diffusion) et que la dislocation ne bouge pas trop vite (vitesse de déformation modérée), les atomes peuvent rejoindre la dislocation et l'épingler à nouveau. On constate donc des oscillations sur la courbe de traction, c'est le « phénomène de Portevin-Lechatelier ».
Lorsque la dislocation est fortement épinglée sur des atomes immobiles, seule la partie centrale va bouger, elle va donc se courber. Si elle se courbe jusqu'à ce que ses branches se touchent, il se forme une dislocation circulaire qui va bouger librement. On a ainsi un phénomène de multiplication des dislocations, le « mécanisme de Frank et Read », qui explique l'écrouissage.
Dislocation et joint de grain[modifier | modifier le code]
La transmission d'une dislocation au travers d'un joint de grain peut être définie par les quatre mécanismes suivants [11]:
- transmission directe avec un plan de glissement ayant le même vecteur de Burgers (le joint de grain est transparent, pas d'effet de durcissement) ;
- transmission directe avec un plan de glissement ayant un vecteur de Burgers différent (une dislocation résiduelle au joint de grain est créée) ;
- transmission indirecte avec un plan de glissement ayant un vecteur de Burgers différent (une dislocation résiduelle au joint de grain est créée) ;
- aucune transmission et le joint de grain joue le rôle d'une barrière impénétrable, ce qui provoque un empilement de dislocations au joint de grain.
Interaction avec des précipités[modifier | modifier le code]
Deux cas différents peuvent se produire lorsqu'une dislocation rencontre un précipité et tente donc de le cisailler pour passer au-travers :
- Le précipité est suffisamment petit pour pouvoir être cisaillé par la dislocation. Cependant, le précipité va exercer une force de rappel sur la dislocation qui tente de le cisailler en se déplaçant et cette force sera d'autant plus grande que le précipité est gros. Cette force est notamment due au champ de contraintes entourant le précipité du fait de sa non-homogénéité avec la matrice. De ce fait, la dislocation aura de plus en plus de mal à progresser et se déformera de plus en plus. Plus difficilement la dislocation passera à travers le précipité, plus dur sera le matériau concerné puisque c'est justement la difficulté de mouvement des dislocations au sein d'un matériau qui est responsable de sa dureté.
- Le précipité est trop gros pour que la dislocation puisse le cisailler. Dans ce cas, la dislocation va se refermer de plus en plus sur elle-même en tentant de cisailler et contourner le précipité jusqu'à se refermer totalement, formant ainsi une nouvelle ligne de dislocation devant le précipité tout en laissant une petite dislocation autour du précipité : c'est ce qu'on appelle le mécanisme d’Orowan et c'est un des mécanismes de multiplication des dislocations. Dans ce cas-ci, la dureté de l'échantillon va diminuer avec la taille du précipité.
En résumé, on peut dire que la dureté du matériau va d'abord augmenter avec la taille des précipités puis diminuer, en passant par un maximum, un pic de dureté correspondant à un état du matériau dit état T6. En général, on favorisera les échantillons comportant des précipités légèrement plus gros que ceux que l'on trouverait à l'état T6 pour éviter tout mécanisme de cisaillement, ce qui aurait pour effet de réduire la taille des précipités, et donc de réduire la dureté du matériau.
Dans le cas où l'échantillon contient plusieurs familles de précipités de tailles différentes, deux par exemple, la dureté du matériau dépendra de la taille relative et de la position des pics de dureté correspondant à chaque famille de précipités.
Si un des deux pics est clairement plus petit que l'autre (i.e. : une des deux courbes de dureté est toujours inférieure à l'autre), la dureté du matériau sera celle qui est donnée par la courbe la plus haute.
Si par contre les deux pics sont de hauteur voisine mais correspondent à différents diamètres de précipités, la dureté suivra l'enveloppe des deux courbes de dureté, c'est-à-dire qu'elle prendra le maximum des deux valeurs donnés par les courbes pour chaque diamètre de précipités. On aura alors une courbe globale de dureté divisée en 4 phases : une croissante (mécanisme de cisaillement) jusqu'au premier pic, puis décroissante (mécanisme d'Orowan) jusqu'à l'intersection des deux courbes ; à nouveau croissante jusqu'au second pic et enfin une deuxième fois décroissante.
Arrangement de dislocations[modifier | modifier le code]


La photo de droite présente un empilement de dislocations dans un monocristal de fluorure de lithium déformé par compression verticale. Les zones en compression, parallèles au plan de glissement, sont en vert et les zones en traction en rouge.
Le point d'inversion des couleurs correspond à un changement de signe des dislocations coin, c'est-à-dire à une source de dislocations coin. Le vecteur de Burgers des dislocations est incliné à 45°. Les dislocations individuelles peuvent être observées grâce aux figures d'attaque qui se traduisent par des petites pyramides à la surface du cristal le long du plan de glissement.
La largeur de l'éprouvette est de quelques millimètres et le nombre total de dislocations dans le plan de glissement de quelques milliers. Le cristal de LiF étant un cristal ionique analogue au sel NaCl, on observe des charges électriques négatives sur la source et positives à l'intersection du plan de glissement et de la surface.
En général, il y a de nombreux plans de glissement. Il est exceptionnel de n'en avoir qu'un seul comme sur la photo[12].
Observation[modifier | modifier le code]
Microscope électronique en transmission (MET)[modifier | modifier le code]

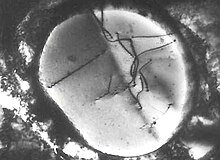
Un microscope électronique en transmission peut être utilisé pour observer des dislocations dans la microstructure d'un matériau[13]. Des lames très minces de matériau sont préparées pour les rendre transparentes au faisceau d'électrons du microscope. Le faisceau électronique subit une diffraction par les plans cristallins du cristal pour former une figure de diffraction et un contraste est généré dans l'image par cette diffraction (ainsi que par les variations d'épaisseur, les variations de déformation et d'autres mécanismes). Les dislocations ont une structure atomique locale différente et produisent un champ de déformation, et conduiront par conséquent les électrons à diffracter d'une façon différente. On remarquera le contraste "ondulé" caractéristique des lignes de dislocation lorsqu'elles traversent l'épaisseur du matériau dans les images. Il faut noter également qu'une dislocation ne peut se terminer au sein d'un cristal ; dans ces images, les lignes de dislocation se terminent à la surface de l'échantillon. Une dislocation ne peut être contenue dans un cristal que si elle forme une boucle fermée.
Les dislocations n'ont pas des structures aléatoires, la structure atomique locale d'une dislocation est déterminée par son vecteur de Burgers. Une application très utile du MET pour imager les dislocations est sa capacité à déterminer expérimentalement la direction du vecteur de Burgers. La détermination du vecteur de Burgers est faite par ce qui appelé une analyse ("g dot b")[14]. Quand on réalise un champ sombre au MET, une tache diffractée est sélectionnée pour former l'image (comme indiqué ci-dessus, les plans du réseau diffractent le faisceau pour former des taches), et l'image est formée par les seuls électrons qui ont été diffractés par le plan responsable de cette tache de diffraction. Le vecteur du schéma de diffraction issu de la tache transmise à la tache diffractée est le vecteur . Sans entrer dans les détails de la microscopie électronique, le contraste d'une dislocation est fonction du produit scalaire de ce vecteur et du vecteur de Burgers (). Donc, si le vecteur de Burgers et le vecteur sont perpendiculaires, la dislocation n'émettra pas de signal et la dislocation n'apparaitra pas du tout dans l'image. Par conséquent, en examinant différentes images en champ sombre formées à partir de taches ayant différents vecteurs g, le vecteur de Burgers peut être déterminé.
Par ailleurs, certains microscopes permettent également le chauffage et/ou la déformation in-situ d'échantillons, permettant donc l'observation directe du mouvement des dislocations et de leurs interactions.
Autres méthodes[modifier | modifier le code]
Les techniques de microscopie ionique à effet de champ et de sonde atomique tomographique sont des méthodes permettant d'obtenir des amplifications beaucoup plus élevées (typiquement 3 millions de fois ou plus) et permettent l'observation des dislocations au niveau atomique. Quand le relief de surface peut être résolu au niveau de la marche atomique, les dislocations vis apparaissent comme des structures spiralées distinctes – révélant donc un important mécanisme de la croissance cristalline : lorsqu'il existe une marche de surface, des atomes peuvent plus facilement ajoutés au cristal, et la marche de surface associée à une dislocation vis n'est jamais détruite quel que soit le nombre d'atomes que y sont ajoutés.
(Par comparaison, la microscopie optique traditionnelle, qui n'est pas appropriée pour l'observation "directe" des dislocations, offre typiquement des amplifications allant seulement jusqu'à environ 2000 fois).
Quand une ligne de dislocation coupe la surface d'un matériau métallique, le champ de déformation associé accroît localement la susceptibilité relative du matériau à une attaque acide et un puits de gravure de forme géométrique régulière se forme. Si le matériau est déformé et re-gravé à plusieurs reprises, une série de puits de gravure peut être produite ce qui trace de manière effective le mouvement de la dislocation en question.
Après gravure chimique, de petits puits (puits de gravure) sont formés lorsque la solution de gravure attaque préférentiellement la surface de l'échantillon autour des dislocations interceptant cette surface, à cause de l'état plus fortement déformé du matériau. Donc, les caractéristiques de l'image indiquent les points où les dislocations interceptent la surface de l'échantillon. De cette façon, les dislocations dans le silicium, par exemple, peuvent être observées indirectement à l'aide d'un microscope à contraste interférentiel. L'orientation cristalline peut être déterminée par la forme des puits de gravure associés aux dislocations (dans le cas des illustrations ci-dessous : 100 = elliptique, 111 = triangulaire/pyramidale).
-
Puits de gravure formés aux extrémités de dislocations dans du silicium, orientation 100
-
Puits de gravure formés aux extrémités de dislocations dans du silicium, orientation 111
-
Puits de gravure formés aux extrémités de dislocations dans du silicium, orientation 111
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- c'est-à-dire non-ponctuel
Références[modifier | modifier le code]
- Cf. C. S. Barrett (trad. C. Lemoynie), Structure des métaux [« Structure of Metals »], Mc-Graw Hill, (réimpr. éditions Dunod, 1957), « Théorie des dislocations », p. 372
- Cf. Joël Douin, Mécanique des milieux continus : Introduction à la plasticité des matériaux, Diderot, coll. « Pavages », (ISBN 2843520355), « 4.6 Théorie élastique des dislocations rectilignes », p. 71
- Douin 1997, p. 75
- Douin 1997, p. 75
- Cf. Douin 1997, p. 113
- Cf. Philippe Lours, « Au cœur des matériaux cristallins », sur IMT Mines Albi - Institut Clément Ader.
- Douin 1997, p. 84
- Douin 1997, p. 72
- Douin 1997, p. 73
- Douin 1997, p. 79
- A.P. Sutton and R.W. Balluffi (1995), "Interfaces in Crystalline Materials.", OUP Oxford, (ISBN 978-0199211067).
- Bernard Schaeffer, Étude photoélastique d'un empilement de dislocations dans LiF coloré. Bull. Soc. Franç. Minér. Crist., 89, 297 (1966).
- J. C. H. Spence, « Imaging dislocation cores – the way forward », Phil. Mag., vol. 86, , p. 4781 (DOI 10.1080/14786430600776322, Bibcode 2006PMag...86.4781S)
- Carter, C. Barry., Transmission electron microscopy : a textbook for materials science, Springer, , 775 p. (ISBN 978-0-387-76502-0, OCLC 660999227, lire en ligne)
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Jacques Friedel, Les dislocations, Paris, Gauthier-Villars, 1956
- Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], [détail des éditions]
- Physique des solides (Ashcroft, Mermin)
- RF N. Nabarro, Dislocations (Dover)
Liens externes[modifier | modifier le code]
- Déformation plastique et dislocations
- Boite à outils Matlab pour l'analyse du transfert de plans de glissement au travers de joints de grains














