Courbe de Laffer

La courbe de Laffer est une hypothèse faite dans le cadre de modélisations économiques et développée par des économistes de l'offre, en particulier Arthur Laffer. Elle formalise l'idée que les effets favorables d'un taux d'imposition élevé sur la croissance des recettes de l'État (l’État étant pris ici au sens large, incluant toutes les administrations publiques) disparaîtraient lorsque le taux d'imposition devient « trop élevé » (sans que ce seuil ait pu être défini).
Lorsque les prélèvements obligatoires sont déjà élevés, une augmentation de la pression fiscale conduirait à une baisse des recettes de l'État, parce que la hausse du taux de l'impôt serait plus que compensée par la réduction de son assiette découlant du fait que les agents économiques sur-taxés seraient incités à moins travailler. Cependant les paramètres définissant la notion de sur-taxation ne sont pas définis et sont toujours débattus (absence de consensus sur un seuil spécifique).
Histoire[modifier | modifier le code]
Les premières études sur la relation entre le taux d'imposition et la croissance remontent au XIVe siècle avec les écrits d'Ibn Khaldoun[1],[2].
L'idée que « trop d'impôt tue l'impôt » ou que « le taux mange l'assiette » est ancienne : des économistes libéraux anciens avaient en leur temps déjà mené une réflexion sur ce phénomène, comme Adam Smith qui suggérait le phénomène en écrivant : « L'impôt peut entraver l'industrie du peuple et le détourner de s'adonner à certaines branches de commerce ou de travail » ; et surtout Jean-Baptiste Say qui concluait qu'« un impôt exagéré détruit la base sur laquelle il porte »[3]. L'économiste français poursuit en précisant : « Par une raison contraire, une diminution d'impôt, en multipliant les jouissances du public, augmente les recettes du fisc et fait voir aux gouvernements ce qu'ils gagnent à être modérés[3]. »
Frédéric Bastiat écrivit : « Si un impôt est graduellement et indéfiniment élevé, par cela même qu'à chaque degré d’élévation il restreint un peu plus la consommation ou la matière imposable, un moment arrive nécessairement où la moindre addition à la taxe diminue la recette. »[4]
Mais il revient à l'économiste américain Arthur Laffer, à la fin des années 1970, d'avoir tenté de théoriser ce qu'il nommait « l'allergie fiscale », et de l'avoir popularisée (au point qu'elle est évoquée dans le débat et les choix politiques), à l'aide de la courbe qui porte son nom. L'histoire répandue est que Laffer dessina la courbe pour la première fois en 1974, sur une nappe de restaurant à Washington, alors qu'il dînait en compagnie de Donald Rumsfeld, son assistant Dick Cheney et le journaliste Jude Wanniski (en) du Wall Street Journal. Ce dernier qui popularisa la théorie, ne dément ni ne confirme cette origine[5],[2].
La courbe a été utilisée par les théoriciens libéraux de l'offre, pour lesquels le moyen d'action essentiel d'un État passe par la réduction des impôts. Cette politique économique, en diminuant le poids de l'imposition et des cotisations sociales sur les entreprises et la population, réduirait ce que ces auteurs considèrent comme une pénalisation du travail et de l'épargne. Il conviendrait, parallèlement, de diminuer les compétences de l'État-providence, qui sont généralement à l'origine de la hausse des impôts, et de diminuer l'endettement de la sphère publique. Ce fut la thèse centrale des reaganomics, politique du président Ronald Reagan (États-Unis) et de Margaret Thatcher (Royaume-Uni) dans les années 1980.
Présentation[modifier | modifier le code]
Pour simplifier, la courbe est bâtie sur l'hypothèse d'une économie fermée (où les échanges avec l'extérieur sont ignorés) ; mais prendre en compte l'ouverture des frontières ne change rien au résultat de Laffer, puisqu'elle donne aux individus sur-taxés des possibilités d'évasion fiscale qui ne peuvent qu'accentuer la diminution des recettes de l'État en cas d'imposition trop forte. En outre, l'importance de l'attractivité fiscale lorsque les taux d'imposition sont bas (en particulier pour ce qui concerne l'impôt sur les sociétés) peut mener à l'implantation de nouvelles sociétés et ainsi augmenter la base de l'impôt.
Hypothèse[modifier | modifier le code]
Une hypothèse est faite sur la rationalité des agents économiques : lorsque le taux d'imposition est trop fort, les agents diminuent leur travail. Poussé à l’extrême, ce raisonnement implique que les agents cesseraient de travailler si le taux d'imposition était de 100 % : de même qu'avec un taux d'imposition nul, « à un taux d'imposition de 100 %, le gouvernement ne percevrait également aucun revenu fiscal parce que personne ne travaillerait volontairement pour un salaire après impôts nul (autrement dit, il n'y aurait pas d'assiette fiscale) »[2]. Le niveau du seuil d’imposition au-delà duquel l'effet de la diminution de l'offre de travail des agents outrepasse celui de l'augmentation du taux est difficile à établir, et dépend des conditions de vie (par exemple, un individu que l'État prive des revenus nécessaires pour satisfaire ses besoins primaires aura tendance à travailler davantage et à s'investir dans le travail au noir).
Implications de l'hypothèse[modifier | modifier le code]


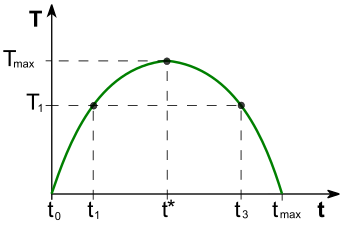
Selon ce modèle, il existerait alors un niveau maximal du produit de l'impôt, au taux d'imposition (voir graphique) au-delà duquel le produit de l'impôt diminue lorsque le taux d'imposition augmente, puisque cette hausse du taux est plus que contrebalancée par la baisse de l'assiette fiscale sur laquelle il s’applique.
On peut illustrer cette relation entre niveau et produit de l'impôt par une courbe parabolique, comme celle ci-contre, même si dans la réalité :
- il peut y avoir plusieurs maxima locaux (il en existe au moins un, mais il peut y en avoir plusieurs sans que cela change fondamentalement le résultat de Laffer) ;
- on ne sait que peu de chose sur la courbe. En fait, on sait seulement qu'elle croise la ligne horizontale (revenus fiscaux nuls) aux deux taux de 0 et 100 %, mais pour le reste elle peut très bien présenter des sauts (ne pas être continue), présenter de grandes plages où les variations de taux n'ont que peu d'effet sur les recettes, monter et descendre, faire des boucles (ainsi, un même taux pourrait, selon les conditions, correspondre à plusieurs niveaux de recettes, ceci étant lié aux effets d’hystérèse) ;
- le taux donnant le maximum de revenus fiscaux peut varier au fil du temps, puisque le fonctionnement économique peut changer.
Prolongements[modifier | modifier le code]
La courbe de Laffer est simple à comprendre, et elle illustre l'idée simple qu'il n'est pas fiscalement rentable de dépasser un certain taux de prélèvement. Au-delà, le taux est considéré comme « prohibitif » et désincite à tel point les personnes à travailler qu'il entraîne la baisse des recettes de l'État.
Elle illustre l'idée selon laquelle à partir de l'effet désincitatif sur l'offre de travail l'emporte sur les recettes attendues. Deux effets contradictoires entrent en jeu : selon les néoclassiques et les libéraux, un effet de substitution qui incite un agent à diminuer son temps de travail (occuper son temps à autre chose, voire émigrer), et selon les économistes keynésiens, un effet de revenu qui incite les agents à travailler plus afin de retrouver le niveau de salaire dont ils disposaient avant l'augmentation des impôts. Pour des taux d'imposition « élevés » l'effet de substitution l'emporte sur l'effet de revenu.
Toute la difficulté est de déterminer si un taux donné est « élevé » dans ce sens, et les études empiriques, qui tentent de vérifier cette relation, aboutissent à des résultats controversés. Il est difficile lors d'une étude empirique de séparer les nombreux facteurs qui entrent en jeu, comme :
- les besoins de l'État qui peuvent être différents ou non constants ;
- la structure des prélèvements obligatoires et la façon dont ils sont perçus auprès de la population ;
- l'histoire fiscale du pays, et le niveau habituel des prélèvements pour ce pays ;
- les croyances des agents dans la situation économique future, et le contexte économique général ;
- le niveau d’aversion au risque des investisseurs et des entrepreneurs.
La première partie de la courbe (taux faibles) peut être mise en relation avec le théorème d'Haavelmo.
Si la courbe est continue et dérivable, alors elle présente nécessairement un plateau (théorème de RolleInterprétation abusive ?), c'est-à-dire une zone où de faibles variations du taux d'imposition ont peu d'impact sur les revenus fiscaux. S'il existe une telle zone de revenu à peu près stable pour l'État, alors, pendant que les recettes de l'État stagnent, ceux des contribuables baissent de façon importante au fur et à mesure de la hausse des taux : par exemple (simplifié), si un taux de 50 % rapporte la même chose qu'un taux de 40 %, cela veut dire que les contribuables ont réduit leur production de 100 à 80, mais aussi que la quantité qui leur reste après impôt (et avant redistribution, éventuellement) est passée de 60 à 40. Pour un même revenu fiscal, le taux le plus bas correspond à plus de richesse collective (100 contre 80) et plus de richesses privées (60 contre 40).
Résultats avancés[modifier | modifier le code]
Arthur Laffer a rappelé que les pays baltes et la Russie ont vu leur économie décoller peu après avoir mis en place un impôt à taux unique inférieur à 35 %[2]. Il a également invoqué à l'appui de son hypothèse les succès économiques qui ont suivi la loi sur les impôts Kemp-Roth signée par Ronald Reagan, les baisses d'impôts de John Kennedy et les réformes fiscales de 1997 aux États-Unis, pour illustrer comment la baisse de l'impôt pouvait entraîner une croissance économique et des recettes fiscales[2].
L'économiste Florin Aftalion cite, pour sa part, la situation des États-Unis en 2004-2005 : l'année même où les réductions d'impôt sont entrées en vigueur, les recettes fiscales du gouvernement ont augmenté de 8 % et 9 %. La hausse s'est poursuivie en 2006 : 10 % au premier semestre alors que la croissance de l'économie était de 3,9 % par an[6]. En avril 2006, le Trésor américain a annoncé que les recettes fiscales avaient atteint leur second point le plus haut de l'histoire à la suite des baisses d'impôts de 2003.
L'ancien ministre néo-zélandais Maurice McTigue témoigne d'une autre illustration de l'hypothèse de Laffer, dans les années 1980 : « Ainsi, nous avons réduit de moitié le taux de l'impôt sur le revenu et supprimé un certain nombre de taxes annexes. Paradoxalement, les recettes de l'État ont augmenté de 20 %. Oui ! Ronald Reagan avait raison : réduire les taux de l'impôt a effectivement pour conséquence l'augmentation des recettes fiscales[7]. »
En 2017, Jacob Lundberg de l'Université d'Uppsala a estimé la courbe de Laffer pour 27 pays de l'OCDE, maximisée selon lui par un taux marginal de prélèvement variant entre 60-61% (Autriche, Luxembourg, Pays-Bas, Pologne, Suède) à 74-76% (Allemagne, Suisse, Royaume-Uni, États-Unis). La plupart des États ont un taux marginal en deçà du maximum, alors que cinq pays l'excédent (Autriche, Belgique, Danmark, Finlande, Suède)[8].
Critiques[modifier | modifier le code]
La courbe de Laffer est critiquée par de nombreux économistes. Ainsi, pour Raphaël Didier[9], ce n'est qu'une vague intuition qui n'a jamais été démontrée, une « idée zombie » qui resurgit périodiquement lors des campagnes électorales. Si personne ne nie qu'un taux d'imposition de 100 % réduirait les recettes de l'État comme peau de chagrin, l'évolution de la relation aux alentours supposés du taux d'imposition optimal est remise en question. La répartition des impôts selon les catégories sociales rend cette relation complexe[10]. Les économistes critiques, comme le néo-keynésien Joseph E. Stiglitz (Quand le capitalisme perd la tête), reprochent à Laffer d'avoir présenté une courbe dont la forme est en fait inconnue, sans études empiriques spécifiques pour en déterminer les points notables. Le journaliste scientifique Martin Gardner a tourné en dérision l'habillage mathématique des discours sur les prévisions économiques, et rappelé le précédent de la « courbe de Phillips », chère à Nixon dès les années 1950[11].
Selon des théoriciens non libéraux comme Peter Lindert, l'exemple des pays scandinaves, où l'imposition a pu dépasser les 70 % du PIB sans entraîner les conséquences que prévoyait Laffer, montrerait que si la courbe de Laffer s'y appliquait, le niveau d'imposition pour l'atteindre serait très élevé et n'aurait donc jamais été atteint à ce jour par un quelconque pays. Étant donné les niveaux d'imposition actuels (entre 30 et 50 % du PIB), la majorité des pays se situeraient dans la première partie de la courbe ou dans sa partie plate (où une augmentation des impôts n'augmente pas les recettes totales de l'État, mais diminue le bien-être des agents taxés).
Par ailleurs, les exemples historiques qui, pour ses défenseurs, illustrent l'efficacité de la courbe de Laffer, sont considérés comme non probants par ses détracteurs, le lien causal n'ayant pas été démontré, et explicables par d'autres éléments de la conjoncture. Ainsi, un article de 2012 explique le renforcement de la croissance américaine à partir de 2006 par un creux cyclique les années précédentes[12].
Notes et références[modifier | modifier le code]
- Jalel Berrebeh, « Fiscalité ; partie 1, La théorie générale de l'impôt » [PDF], sur Faculté des Sciences Économiques et de Gestion de Nabeul, 1998-1999 (consulté le ), p. 8
- (en) Arthur Laffer, « The Laffer Curve: Past, Present, and Future », sur The Heritage Foundation, .
- Traité d'économie politique, chapitre IX, livre III, 1821, Calmann-Lévy, Paris, réédition 1972, cité dans Philippe Simonnot, 39 leçons d'économie contemporaine, éd. Gallimard, Folio actuel, 1998, pp. 393 et 396
- « Page:Œuvres complètes de Frédéric Bastiat, Guillaumin, 2.djvu/201 - Wikisource », sur fr.wikisource.org (consulté le )
- Muriel Motte, « Arthur Laffer ou l'efficacité fiscale », sur L'Opinion,
- L'économie de l'offre se porte bien - Florin Aftalion, Liberte-cherie.com
- Réduire l'État a ses justes proportions : la Nouvelle-Zélande - Maurice McTigue, Objectifliberte.fr, 5 juillet 2011
- (en) Jacob Lundberg, Department of Economics and Uppsala Center for Fiscal Studies, Université d'Uppsala, « The Laffer curve for high incomes », Luxembourg Income Study,
- « Raphaël DIDIER explique l’économie », sur Raphaël DIDIER explique l’économie (consulté le ).
- Thomas Piketti et Emmanuel Saez, Pour une révolution fiscale. Un impôt sur le revenu pour le XXIe siècle, France, Le Seuil-La République des idées, , 133 p. (ISBN 978-2-02-103941-2 et 2-02-103941-2)
- (en) Martin Gardner, « The Laffer curve and other laughs in current economics », Scientific American, vol. 245, no 6, , p. 18-34 ; repris dans le recueil Martin Gardner, The Night Is Large: Collected Essays, 1938-1995, St. Martin's Press, , 608 p.
- (en) Do Tax Cuts Lead to Economic Growth? - David Leonhardt, The New York Times, 15 septembre 2012
Annexes[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Austan Goolsbee, Robert E. Hall, et Lawrence F. Katz, « Evidence on the High-Income Laffer Curve from Six Decades of Tax Reform » , Brookings Papers on Economic Activity, Brookings Institution Press, no 2, 1999, pp. 1-64 [présentation en ligne]
- (en) James M. Buchanan et Dwight R. Lee, « Politics, Time, and the Laffer Curve », Journal of Political Economy, University of Chicago Press, vol. 90, no 4, août 1982, pp. 816-819 [présentation en ligne]







