Ovale de Cassini

En mathématiques, un ovale de Cassini est un ensemble de points du plan tel que le produit des distances de chaque point P de l'ovale à deux autres points fixés P1 et P2 est constant, c’est-à-dire de telle sorte que le produit
soit constant. Les points P1 et P2 sont appelés les foyers de l'ovale.
Les ovales de Cassini portent le nom de Giovanni Domenico Cassini.
Si l'on note b2 le produit constant qui précède, et a la demi-distance entre les foyers,
la forme de l'ovale dépend du rapport b/a.
- Si b/a est plus grand que 1, le lieu est une boucle simple et continue.
- Si b/a est plus petit que 1, le lieu est composé de deux boucles non sécantes.
- Si b/a est égal à 1, le lieu est une lemniscate de Bernoulli.
Équations[modifier | modifier le code]
Si les foyers des ovales sont de coordonnées (a, 0) et (−a, 0), l'équation de la courbe est donnée par
Ou, en coordonnées polaires :
Propriétés[modifier | modifier le code]
Trajectoires orthogonales[modifier | modifier le code]
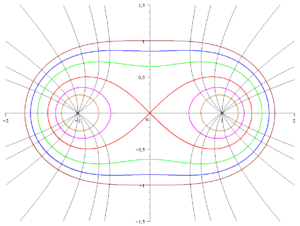
Les ovales de Cassini sont les trajectoires orthogonales aux hyperboles équilatères de centre (0, 0) et passant par le point (1, 0).
En effet, l'équation de cette famille d'hyperboles est
Elle est solution de l'équation différentielle :
Ce qui donne l'équation différentielle des trajectoires orthogonales :
Les trajectoires orthogonales sont donc d'équation
et on retrouve bien l'équation des ovales de Cassini.
Sections planes d'un tore[modifier | modifier le code]

On obtient des ovales de Cassini par intersection d'un tore par un plan parallèle à son axe et à une distance égale au rayon du cercle générateur.
Généralisations[modifier | modifier le code]
On peut faire de même avec plus de deux foyers, ou plus de deux dimensions.
Par exemple, un ovale de Cassini à n foyers est l'ensemble des points P vérifiant :
Cette définition s'étend naturellement à l'espace, ce qui définit une surface implicite.
-
Ovale de Cassini à trois foyers.
-
Surface de Cassini à 6 foyers.
Liens externes[modifier | modifier le code]
- (en) Eric W. Weisstein, « Cassini Ovals », sur MathWorld
- Robert Ferréol, « Ovale de Cassini », sur Encyclopédie des formes mathématiques remarquables










