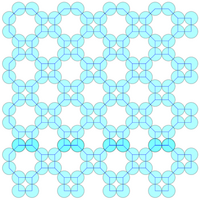
Empilement de cercles

Un article de Wikipédia, l'encyclopédie libre.
Il n'est pas évident de regrouper des cercles de tailles différentes de la façon la plus compacte.

En géométrie, un empilement de cercles ou empilement de disques est un arrangement de cercles ou de disques, de tailles identiques ou non, dans un domaine donné, de telle sorte qu'aucun chevauchement ne se produise et qu'aucun cercle/disque ne puisse être agrandi sans créer de chevauchement. On se pose à leur sujet divers problèmes comme la recherche d'empilements de densité maximale, ou au contraire, minimale.

Définitions[modifier | modifier le code]

Un empilement d'une partie fermée X du plan euclidien dont toute intersection avec un disque est quarrable (i.e. possède une aire), est un ensemble de cercles de rayons non nuls inclus dans X dont les disques fermés associés ont les propriétés suivantes :

- deux disques de l'empilement sont tangents ou d'intersection vide,

- tout disque est tangent à au moins un autre.

L'empilement est dit localement rigide (localy jammed en anglais) si tout disque est coincé par ses voisins, autrement dit si deux disques tangents à un disque D sans aucun autre disque tangent à D entre eux ont des centres formant un angle aigu avec le centre de D [1].

L'empilement est dit compact si tout disque tangent à un disque D est tangent à deux autres disques tangents à D ou ce qui est équivalent, si le graphe planaire dont les sommets sont les centres des disques et les arêtes les segments joignant les centres de deux disques tangents a des faces triangulaires [2].

Empilement complet de cercles dans un triangle.

La densité d'un empilement est le rapport de l'aire couverte par les disques à l'aire de la partie X (si X est non bornée, c'est la limite, si elle existe, de la densité de l'intersection avec un disque de rayon tendant vers l'infini).

L'empilement est dit complet si on ne peut lui rajouter de disque, autrement dit si sa densité est égale à 1 [3].

Un empilement est forcément dénombrable ou fini, tout disque contenant un point à coordonnées rationnelles.

Cercles de même taille dans le plan[modifier | modifier le code]

Empilement le plus dense[modifier | modifier le code]

Article détaillé : Empilement_compact#Empilement_compact_de_cercles_identiques.
Cercles identiques d'un empilement hexagonal, empilement le plus dense.

Dans le plan euclidien, Joseph Louis Lagrange a prouvé en 1773 que l'empilement de cercles de même rayon le plus dense est l'empilement hexagonal [4] : les centres des cercles sont disposés en un réseau hexagonal (rangées décalées, comme un nid d'abeille) ; chaque cercle est entouré de 6 autres. Sa densité est de  ; voir la suite A093766 de l'OEIS.

Il avait supposé que les centres des cercles formaient un réseau du plan. Sans cette supposition, Axel Thue donne une preuve incomplète du théorème en 1910, Toth en donne une preuve complète en 1943, et Chang et Wang une preuve en moins de 4 pages en 2010 [4],[5],[6].

Autres empilements[modifier | modifier le code]

À l'autre extrême, Böröczky a démontré en 1964 qu'il existe des empilements de cercles de même rayon d'une partie bornée du plan, localement rigides, de densité arbitrairement faible [7],[1].

Pour le plan tout entier, la densité la plus faible pour de tels empilements serait égale à [8].

Il existe 11 empilements de cercles de mêmes rayons basés sur les 11 pavages réguliers ou semi-réguliers du plan, obtenus en dessinant des cercles identiques centrés aux sommets du pavage [8],[9].

Cercles de deux tailles données dans le plan[modifier | modifier le code]

Empilement binaire compact de cercles avec deux types de cercles de tailles les plus proches possibles [2]. C'est aussi l’empilement binaire le plus dense de disques avec ce rapport de taille (rapport de 0,6375559772 avec une densité de 0,910683) [10].

Un problème concernant les empilements consiste à trouver la densité maximale d'un empilement comportant des cercles de deux tailles différentes (un empilement binaire). Seules neuf possibilités pour les rapports des rayons des deux types de cercles permettent un empilement compact [2]. Pour ces neuf rapports de rayons, on connaît un empilement compact qui atteint la densité maximale théorique, laquelle est plus forte que celle de l'empilement optimal des disques de même taille [11],[12].

On sait également que si le rapport des rayons est supérieur à 0,742, un empilement binaire compact est toujours moins dense que l'empilement optimal des disques de même taille[10],[13].

Un exemple avec cinq tailles de cercles dans le plan[modifier | modifier le code]

L'empilement présenté ci-contre est issu d'une œuvre réalisée par Daniel Buren, dénommée "Excentrique(s), travail in situ", qu'il a réalisée au Grand Palais à Paris en 2012. Elle est issue d'un pavage du Palais de l'Alhambra à Grenade.

L'empilement comporte cinq types de cercles dont les rapports des rayons ont des expressions irrationnelles complexes. Sa densité est de 0,908 environ[14].

Cercles de même rayon dans des domaines bornés[modifier | modifier le code]

Quinze cercles identiques empilés dans le plus petit carré possible. Il existe seulement quatre arrangements de ces cercles en triangles équilatéraux.
On peut placer N biscuits ronds de rayon 1 dans une boite rectangulaire de taille N x 4, mais pour , on peut en placer [15].

Empiler des cercles de même rayon dans des parties bornées simples est un problème courant en mathématiques récréatives. La frontière de la partie jouent alors un rôle important, et le remplissage hexagonal n'est généralement pas optimal lorsqu'il y a un petit nombre de cercles[16].

Voir les pages wikipedia suivantes :

Voir aussi[modifier | modifier le code]

Références[modifier | modifier le code]

  1. ↑ a et b (en) Kahle, « Sparse locally-jammed disk packings », Annals of Combinatorics, vol. 16, no 4,‎ , p. 773–780 (DOI 10.1007/s00026-012-0159-0, S2CID 1559383, lire en ligne)
  2. ↑ a b et c Tom Kennedy, « Compact packings of the plane with two sizes of discs », Discrete and Computational Geometry, vol. 35, no 2,‎ , p. 255–267 (DOI 10.1007/s00454-005-1172-4, arXiv math/0407145, S2CID 11688453)
  3. ↑ (en) Peter Sarnak, « Integral Apollonian Packings », American Mathematical Monthly,‎ (lire en ligne)
  4. ↑ a et b (en) Hai-Chau Chang, Lih-Chung Wang, « A Simple Proof of Thue’s Theorem on Circle Packing », Arxiv,‎ (lire en ligne)
  5. ↑ David Gontier, « EMPILEMENT DE SPHÈRES/BOULES, RÉSULTATS DE MARYNA VIAZOVSKA », Publications école polytechnique,‎ (lire en ligne)
  6. ↑ Thomas Fernique, « Empilements de disques de densité maximale »,
  7. ↑ Böröczky, « Über stabile Kreis- und Kugelsysteme », Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, Sectio Mathematica, vol. 7,‎ , p. 79–82
  8. ↑ a et b David wells, Le dictionnaire Penguin des curiosités géométriques, Eyrolles, , p. 73 (1), 37 (2)
  9. ↑ (en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, (ISBN 0-486-23729-X, lire en ligne), p. 35-39
  10. ↑ a et b Heppes, « Some Densest Two-Size Disc Packings in the Plane », Discrete and Computational Geometry, vol. 30, no 2,‎ , p. 241–262 (DOI 10.1007/s00454-003-0007-6)
  11. ↑ Bédaride et Fernique, Thomas, « Density of Binary Compact Disc Packings », Arxiv,‎ (arXiv 2002.07168)
  12. ↑ Kennedy, « Circle Packings », (consulté le )
  13. ↑ de Laat, de Oliveira Filho, Fernando Mario et Vallentin, Frank, « Upper bounds for packings of spheres of several radii », Forum of Mathematics, Sigma, vol. 2,‎ (DOI 10.1017/fms.2014.24, arXiv 1206.2608, S2CID 11082628)
  14. ↑ Romain Attal, « Formes mathématiques : Excentrique(s) mais », Revue du Palais de la Découverte, no 382,‎ septembre - octobre 2012, p. 40-45 (lire en ligne)
  15. ↑ David Gontier, « Les biscuits dans la boite »
  16. ↑ (en) « Packomania »

Bibliographie[modifier | modifier le code]

Notices d'autoritéVoir et modifier les données sur Wikidata :
v · m
Empilement
Empilement de cercles
Empilement de sphères
Empilement de carrés
Autres empilements
Puzzles
Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Empilement_de_cercles&oldid=213520634 ».