Crénelage

Le crénelage ou effet d'escalier est un effet visuel caractérisé par des motifs en forme d’escalier sur les contours obliques des dessins. Il se rencontre en infographie, télévision, impression matricielle, image tramée en imprimerie, point de croix, et généralement dans toutes les formes de visualisation composées de figures de couleur uniforme régulièrement espacées, quand cet espacement est suffisamment grand pour que l'élément de base soit visible et que le contour n'est pas parallèle à l'alignement des points. Il est d'autant plus visible que le contraste est élevé.
L’anglicisme aliasing désigne, outre l'effet d'escalier, toutes les formes de repliement de spectre, notamment ceux liés à l'échantillonnage du signal.
Terminologie[modifier | modifier le code]
Le terme « effet d'escalier », désigne en sciences naturelles la répétition d'effets de seuil. Il s'applique aussi depuis longtemps à l'apparence des lignes faiblement obliques des tapisseries, des images tramées de l'imprimerie et de celles des écrans de télévision analogique, qui analysent l'image en lignes.
Le crénelage est à l'origine un terme d'architecture militaire, désignant la construction de créneaux sur les fortifications. Repris en botanique pour décrire des feuilles à bord découpé et en mécanique pour l'usinage de surfaces dans une forme similaire, décrivant en numismatique la dentelure du bord des monnaies[1], il s'applique à toutes les formes de production d'image tramée, et notamment à celles produites par les ordinateurs.
L'informatique dérive une bonne partie de ses termes de l'anglais. Les techniciens américains ont rapproché l'effet d'escalier des phénomènes de repliement de spectre connus auparavant en radio, dans l'échantillonnage du signal et en télévision avec le phénomène de moiré, et ont repris le terme d’aliasing. Le terme français crénelage, plus descriptif, évite de se prononcer sur la nature du phénomène.
Depuis 1990, la règle veut que l'on place un accent grave devant une syllabe articulée sur un e muet. La graphie crènelage est recommandée, mais l'Académie française observe que, comme pour crèmerie, on écrit aussi crénelage avec un accent aigu[2].
Rendu d'images vectorielles[modifier | modifier le code]

Une image informatique finit par être produite sur un périphérique produisant une image matricielle[a]. Ce type d'image est divisé en éléments, généralement rectangulaires et souvent carrés, dont la luminosité et la couleur sont uniformes. Toutes les lignes doivent rentrer dans cette grille, et, quand elle est visible, les lignes obliques présentent un aspect caractéristique et généralement gênant d'escalier[3].
Le crénelage constitue un problème quand on veut tracer une ligne ou un contour avec un fort contraste, comme c'est le cas avec le rendu des images vectorielles, définies par une formule arithmétique ou un algorithme, sans rapport avec la grille de pixels sur laquelle il faudra la faire apparaître.
L'effet d'escalier est maximal quand les pixels ne peuvent prendre que deux valeurs, sombre et clair, comme c'est encore souvent le cas sur une calculatrice de poche à affichage graphique.
L'évolution technologique, en diminuant considérablement la taille des éléments de l'image (pixels), a rendu le crénelage des lignes beaucoup moins apparent, diminuant la fatigue visuelle[4]. La grille d'un écran VGA (1987) a un peu moins d'éléments que celle d'un récepteur de télévision, avec 640 × 480 pixels dans le champ visuel du spectateur. Les écrans des années 2010 en présentent quatre à dix fois plus, ou, quand il s'agit de smartphones, occupent un angle visuel bien plus petit qui rend les pixels indistincts.
L'augmentation de la puissance de calcul des ordinateurs et le déplacement des calculs vers une carte graphique permettent de diminuer le contraste, avec des écrans affichant plusieurs valeurs de gris ou plusieurs couleurs. Des algorithmes anticrénelage (en anglais antialiasing) calculent pour les pixels à proximité de la ligne idéale des valeurs décroissant progressivement.
Tracé de formes géométriques[modifier | modifier le code]

Le crénelage apparaît lorsque l'on trace une forme géométrique sur une image matricielle (rastérisation). La visibilité de ce crénelage dépend de la taille des pixels et de leur contraste. L'algorithme de tracé de segment de Bresenham (1962[5]), premier algorithme de tracé de formes géométriques par exemple, se contente de tracer les pixels les plus proches de l'inclinaison d'un segment de droite sur un bitmap. Si les pixels sont assez grands pour qu'on les distingue et le contraste, élevé, un escalier parait nettement avec ses marches, si la ligne n'est ni horizontale, ni verticale. Ce type d'algorithme a été généralisé des segments rectilignes à toutes sortes de courbes. L'algorithme de tracé de cercle d'Andres (1994) améliore celui de Bressenham (publié en 1977), qui se basait sur celui des ellipses par Jerry Van Aken, publié en 1984, améliorant le travail sur les ellipses et hyperboles de Pitteway (novembre 1967).
Ces algorithmes ont d'abord été mis au point pour le tracé sur imprimante matricielle[5], noir et blanc et ne gérant pas de niveau de gris. Ils ont également été utilisés avec les ordinateurs monochromes, puis, jusque dans les années 1980, avec des profondeurs de couleur de 8 bits, sans utiliser la possibilité de moduler le contraste.
Anticrénelage[modifier | modifier le code]

Les ordinateurs ont ensuite permis d'afficher une palette de couleurs plus étendue. L'anticrénelage a d'abord été effectué sur des images pré-calculées ou dessinées à la main, puis, avec l'augmentation de la puissance des ordinateurs, il a été possible d'ajouter à ces algorithmes le calcul des couleurs intermédiaires au pourtour des changements en diagonale d'une courbe.
L'algorithme de tracé de segment de Xiaolin Wu (juillet 1991) est un des premiers algorithmes de tracé de segments de droites avec anticrénelage. Il réitère son travail la même année avec un algorithme de tracé de cercle avec anticrénelage, publié dans l'ouvrage Graphics Gems II de James Arvo.
Lissage des caractères[modifier | modifier le code]
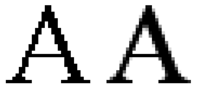
L'application principale des algorithmes anticrénelage est l'affichage du texte. Depuis la fin des années 1980, la plupart des applications qui affichent du texte, comme les navigateurs Web, utilisent des polices de caractères vectorielles, c'est-à-dire décrites par les formules arithmétiques des segments de droites et de courbes qui en forment le contour. Dans ce contexte, on parle de lissage des caractères[6].
L'utilité d'éliminer le crénelage en typographie numérique vient assez tôt ; ces techniques font partie du hinting. Des bibliothèques comme FreeType, chargées de ce travail, prennent généralement en compte l'ordre des points rouges, verts et bleus, sur les pixels des différents types d'écran afin d'affiner la précision de l'anticrénelage. HarfBuzz est une amélioration des procédés de rendu pour les fontes, quel que soit leur sens d'écriture ou leur type de ligature.
En 2002, le W3C envisagea d'intégrer dans les feuilles de style en cascade une propriété font-smooth, qui aurait permis de programmer le lissage ou non des polices de caractères. Cette possibilité a finalement été abandonnée, mais les navigateurs ou les systèmes d'exploitation peuvent laisser cette option[7].
Image animée[modifier | modifier le code]
Dans les applications en temps réel comme les jeux vidéo, pour lesquelles le temps de calcul est limité, le crénelage n'est pas perçu sur les parties en mouvement rapide[8].
Images matricielles[modifier | modifier le code]

Les images que produisent les appareils de photographie numérique ou les scanners, ainsi que les images imprimées tramées sont matricielles.
Photographie numérique[modifier | modifier le code]
Dans les appareils de photographie numérique, le crénelage n'existe pas si les traits obliques de l'image sont flous. Le crénelage se comprend comme un des aspects du problème de l'échantillonnage ; il faut que l'espacement des pixels du capteur soit inférieur à la moitié de la fréquence spatiale la plus élevée fournie par les éléments optiques[b].
On peut supprimer le crénelage des traits obliques, comme le moiré, en augmentant le nombre de capteurs, ou en plaçant un filtre optique pour limiter la résolution. Si par la suite on désire réduire la taille de l'image numérique, il faut au préalable la filtrer pour respecter la même condition[9]. L'algorithme de ré-échantillonnage de Lanczos (en) effectue en une fois les deux opérations. Trois facteurs contribuent à la visibilité des pixels :
- leur taille ;
- le contraste entre deux pixels consécutifs ;
- le temps pendant lequel l'image reste fixe.
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Jack E. Bresenham, « Algorithm for computer control of a digital plotter », IBM Systems Journal, vol. 4, no 1, , p. 25–30 (DOI 10.1147/sj.41.0025, lire en ligne)
- (en) Michael L.V. Pitteway, « Algorithm for Drawing Ellipses or Hyperbolae with a Digital Plotter », The Computer Journal, vol. 10, no 3, , p. 282-289 (ISSN 0010-4620, OCLC 4653069003, DOI 10.1093/comjnl/10.3.282) [PDF]
- Jerry Van Aken, « An Efficient Ellipse Drawing Algorithm », IEEE Computer Graphics and Applications, vol. 4, no 9, , p. 24-35 (ISSN 0272-1716)
- (en) Jack E. Bresenham, « A linear algorithm for incremental digital display of circular arcs », Communications of the ACM, vol. 20, no 2, , p. 100-106 (DOI 10.1145/359423.359432)
- (en) Wu Xiaolin, « An efficient antialiasing technique », ACM SIGGRAPH Computer Graphics, vol. 25, no 4, , p. 143-152 (ISBN 0-89791-436-8, DOI 10.1145/127719.122734, lire en ligne)
- (en) James Arvo (dir.) et Wu Xiaolin, Graphics Gems II, San Francisco, Morgan Kaufmann, , 672 p. (ISBN 978-0-12-064481-0, lire en ligne), « Fast Anti-Aliased Circle Generation », p. 446–450
- Eric Andres, « Discrete circles, rings and spheres », Computers & Graphics, vol. 18, no 5, , p. 695–706 (ISSN 0097-8493, DOI 10.1016/0097-8493(94)90164-3, lire en ligne, consulté le )
- (en) V. Boyer, J.J. Bourdin, Groupe de Recherche en Infographie et d’images -Laboratoire d’Intelligence Artificielle - Univ Paris 8 « Discrete Analysis for Antialiased Lines » () (lire en ligne)
—Eeurographics
Articles connexes[modifier | modifier le code]
Notes et références[modifier | modifier le code]
- Une table traçante pourrait fonctionner de manière purement analogique, mais on n'atteindrait pas la précision qu'on obtient avec un contrôle numérique des mouvements du traceur.
- Voir les détails mathématiques dans Théorème d'échantillonnage de Nyquist-Shannon.
- Jules Adeline, Lexique des termes d'art, nouvelle, (1re éd. 1884) (lire en ligne).
- Maurice Grevisse, La force de l'orthographe, 3, (lire en ligne), p. 358.
- Commission électrotechnique internationale, Electropedia 723-06-92 Diffusion : son, télévision, données. Qualité et défauts de l'image : crénelage.
- (en) Martina Ziefle, « Effects of Display Resolution on Visual Performance », Human Factors: The Journal of the Human Factors and Ergonomics Society, vol. 40, no 4, , p. 554-568 (lire en ligne).
- Bresenham 1962
- « Image numérique » « Image numérique » (version du sur Internet Archive), « La typographie du web » (consulté le ).
- Romy Têtue, « Voir le Web comme au début », (consulté le ).
- (en) William Thompson et al., Visual Perception from a Computer Graphics Perspective, CRC Press, (lire en ligne).
- Exemple sur le site de support technique de Nikon Europe.
