Rosace (mathématiques)

En mathématiques, une rosace, ou rhodonea est une courbe plane obtenue en traçant une sinusoïde en coordonnées polaires.
Généralités[modifier | modifier le code]
À une similitude près, ces courbes sont définies par une équation polaire de la forme :
ou sous forme paramétrique par les fonctions :
k étant un nombre réel :
- si k est rationnel, alors la courbe est fermée et de longueur finie ; Dans ce cas et en considérant , la courbe se fermera lorsque l'angle polaire ;
- Avec si est impair.
- Avec si est pair.
- si k est irrationnel, alors la courbe n'est pas fermée et sa longueur est infinie.
La rosace aura :
- k pétales si k est un entier impair, car la courbe est entièrement tracée quand θ varie de 0 à π (quand θ varie de π à 2π, la courbe repasse par les points déjà tracés) ;
- 2k pétales si k est un entier pair, car la courbe est tracée exactement une fois quand θ varie de 0 à 2π.
- 4k pétales si k est une fraction irréductible de dénominateur 2 (exemples : 1/2, 5/2) ;
- 12k pétales si k est une fraction irréductible de dénominateur 6 et supérieure à 1 (exemples : 7/6, 17/6).
- Rosaces
-
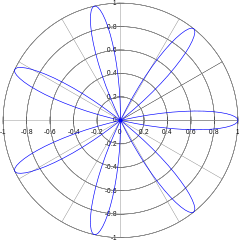
à 7 pétales (k=7) -
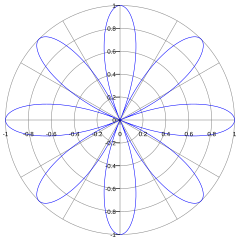
à 8 pétales (k=4) -
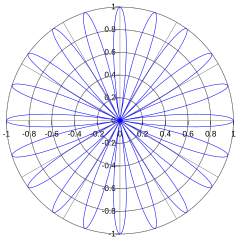
à 20 pétales (k=10)
Si k est une fraction irréductible de dénominateur 3 et supérieure à 1, la rosace aura :
- 3k pétales si son numérateur est impair (exemples : 5/3 et 7/3) ;
- 6k pétales si son numérateur est pair (exemples : 4/3 et 8/3).
Le terme rhodonea a été choisi par le mathématicien italien Luigi Guido Grandi entre 1723 et 1728[1].
Aire[modifier | modifier le code]
Une rosace dont l'équation polaire est de la forme
où k est un entier positif, a une aire égale à
si k est pair et
si k est impair.
Le même principe s'applique aux rosaces d'équation polaire de la forme :
puisque leurs graphes ne sont que des images par rotation des rosaces définies en utilisant le cosinus.
Notes et références[modifier | modifier le code]
- (en) John J. O'Connor et Edmund F. Robertson, « Rhodonea Curves », sur MacTutor, université de St Andrews.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Courbe de Lissajous
- Quadrifolium - une rosace avec k = 2.
- Rosace (topologie) (en)
- Les inverses des rosaces : les épis.
Liens externes[modifier | modifier le code]
- (en) Eric W. Weisstein, « Rose », sur MathWorld
- Rosaces sur Mathcurve