Réponse impulsionnelle

Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

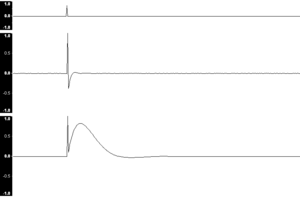
Pour un processus transformant un signal d’entrée en un signal de sortie (signaux électriques par exemple), la réponse impulsionnelle est la sortie qui est obtenue lorsque l'entrée est une impulsion, c'est-à-dire une variation soudaine et brève du signal. En effet, lorsqu'une impulsion est fournie à l'entrée d'un système linéaire, la sortie n'est en général plus une impulsion, mais un signal ayant une certaine durée (parfois infinie comme dans le cas d’un filtre à réponse impulsionnelle infinie (RII)).

Définition mathématique de l’impulsion

Pour un système à temps continu, le modèle mathématique d’une impulsion est une distribution de Dirac.

Pour un système à temps discret (et non le système lui-même), une impulsion est définie par la suite $\delta (n)$ valant 1 si $n = 0$ et 0 sinon.

Dans les deux cas, la réponse impulsionnelle est la sortie du système en réponse à cette impulsion.

Réponse impulsionnelle d'un système linéaire invariant (SLI)

Caractérisation d'un SLI par sa réponse impulsionnelle

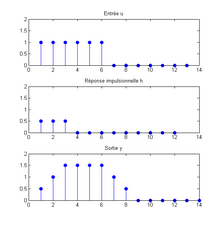
Soit $T$ la représentation mathématique d’un système à temps discret ; à une entrée $x(n)$ correspond une sortie $y(n)$ satisfaisant la relation :

$\{y(n)\} =T\left[ \{x(n)\} \right] .$

$T$ est ainsi une application de l’espace des suites dans lui-même.

Supposons de plus que $T$ soit linéaire et invariant par translation temporelle. Dans ce cas, la réponse impulsionnelle

$\{h(n)\} =T\left[ \{\delta(n)\} \right]$

caractérise entièrement le système puisque la sortie ${y(n)}$ peut être calculée à partir de n’importe quelle entrée ${x(n)}$ en appliquant la relation :

$y(n) =\sum_{k} h(n-k) x(k) = \sum_{k} h(k) x(n-k)\$

Dans le cas continu, cette relation d’écrit :

$y(t) = \int_{-\infty}^{\infty} h(t-\tau) x(\tau) d\tau = \int_{-\infty}^{\infty} h(\tau) x(t-\tau) d\tau.$

Preuve (cas discret)

Remarquons qu'une entrée ${x(n)}$ est une suite d'impulsions discrètes décalées dans le temps. Puisque le système est invariant, le décalage des impulsions produit simplement une sortie elle aussi décalée (voir système invariant). La linéarité du système permet ensuite d’exprimer la sortie ${y(n)}$ par la somme des réponses spécifiques à chacune de ses impulsions.

Considérons alors la contribution à l'instant $n$ de l'impulsion décalée de $k_0$ : pour une entrée $\left\{ x(k_0) \delta (k-k_0) \right\}$, la sortie à l'instant $n$ vaut, $h(n-k_0) x(k_0).\$

La réponse totale s'obtient ainsi en sommant les contributions de toutes les impulsions décalées, soit :

$y(n) =\sum_{k} h(n-k) x(k),\$

un produit de convolution qui, par commutativité, conduit à :

$y(n) =\sum_{k} h(k) x(n-k).\$

Les mêmes arguments permettent de montrer le résultat indiqué pour le cas continu.

Relation avec la fonction de transfert d'un SLI

La transformée de Laplace (respectivement la transformée en Z) de la réponse impulsionnelle $h(t)\$ (respectivement $h(n)\$) d'un système linéaire invariant (SLI) à temps continu (respectivement discret) est égale à la fonction de transfert $H(p)\$ (respectivement $H(z)\$) de ce système.

Pour le démontrer, il suffit d'appliquer les transformées à la relation $y(n) =\sum_{k} h(k) x(n-k)\$ en utilisant le fait qu'un produit de convolution devient un produit dans le domaine fréquentiel.

Voir aussi

• Transformée de Laplace
• Transformée de Fourier
• Transformée en Z
• Système invariant
• Système linéaire
• Réponse indicielle