Fibré de Seifert
En topologie, un fibré de Seifert est une variété de dimension 3 munie d'une « bonne » partition en cercles. Plus précisément, c'est un fibré en cercles sur un orbifold de dimension 2. Ces variétés ont été introduites par Herbert Seifert[1]. La plupart des « petites » variétés de dimension 3 sont des variétés de Seifert, et pour six des huit géométries de Thurston, toute variété orientée compacte sans bord de l'un de ces six types est aussi de Seifert.
Définition[modifier | modifier le code]
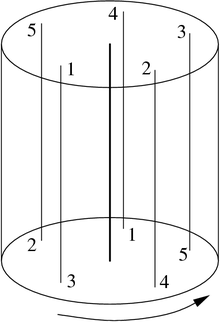
Une variété de Seifert est une variété de dimension 3 compacte sans bord munie d'une partition en cercles (appelés fibres) telle que chaque fibre possède un voisinage tubulaire formant un tore fibré standard.
Le tore fibré standard correspondant à un couple (a, b) d'entiers premiers entre eux avec a > 0 est le tore de la rotation du disque d'angle 2πb/a (muni de sa fibration en cercles naturelle). La fibre centrale est dite ordinaire si a = 1 et exceptionnelle si a > 1.
L'ensemble des fibres forme un orbifold de dimension 2, noté B et appelé la base – ou la surface des orbites – de la fibration. Son espace topologique sous-jacent est une surface B0 dont certains points – ceux qui correspondent aux fibres exceptionnelles – sont des points singuliers de l'orbifold B.
Une variété de Seifert au sens originel ci-dessus (donc compacte) n'a qu'un nombre fini de fibres exceptionnelles. Mais la définition peut être étendue aux variétés non compactes.
Elle peut d'autre part être étendue aux variétés à bord (le bord sera alors aussi un fibré en cercles, donc sera une réunion de tores si la variété est compacte). Également, quand on étudie les variétés non orientables, il est parfois utile d'autoriser, comme voisinage tubulaire, un tore de réflexion du disque (au lieu d'un tore de rotation), i.e. une bouteille de Klein solide fibrée (au lieu d'un tore solide fibré standard), auquel cas les fibres exceptionnelles peuvent former des familles à un paramètre (au lieu d'être isolées)[2]. Dans ces deux cas, la base B de la fibration est un orbifold à bord.
Classification[modifier | modifier le code]
Herbert Seifert a classifié tous les fibrés de Seifert (compacts, sans bords) en termes des invariants suivants. À chacun de ces fibrés est associée de façon unique une liste normalisée de symboles de la forme :
où
- ε est l'un des 6 symboles o1, o2, n1, n2, n3, n4 (respectivement : Oo, No, NnI, On, NnII, NnIII dans la notation originelle de Seifert), et est égal à :
- o1 si B et M sont orientables,
- o2 si B est orientable et M est non orientable,
- n1 si B et M sont non orientables et tous les générateurs de π1(B) préservent l'orientation de la fibre,
- n2 si B est non orientable et M est orientable, ce qui entraîne que tous les générateurs de π1(B) renversent l'orientation de la fibre,
- n3 si B et M sont non orientables et g ≥ 2 et exactement 1 générateur de π1(B) préserve l'orientation de la fibre,
- n4 si B et M sont non orientables et g ≥ 3 et exactement 2 générateurs de π1(B) préservent l'orientation de la fibre ;
- g est le genre de la 2-variété sous-jacente à la surface des orbites ;
- b est un entier, soumis de plus aux restrictions que b ne peut valoir que 0 ou 1 si M est non orientable et même, b ne peut valoir que 0 si de plus l'un des a'i vaut 2 ;
- {{(a1,b1),...,(ar,br)}} est le multiensemble (i.e. la liste non ordonnée et avec répétitions éventuelles, mais les accolades qui le précisent sont généralement omises) des couples d'entiers qui déterminent le type de chacune des r orbites exceptionnelles. Ils sont normalisés de telle façon que 0 < bi < ai si M est orientable, et 0 < bi ≤ ai/2 sinon.
Le fibré de Seifert correspondant à la liste (b,(ε,g);(a1,b1),...,(ar,br)) peut être construit à partir de celui qui correspond à la liste (0,(ε,g);) par « chirurgie », en découpant r + 1 tores pleins fibrés sans fibre singulière et en recollant à leur place des tores fibrés standards de types (1,b),(a1,b1),...,(ar,br).
Si l'on s'affranchit des conditions de normalisation alors on peut effectuer les modifications suivantes sur la liste des symboles, sans que cela change le fibré de Seifert qu'elle représente :
- changer à la fois le signe d'un ai et celui du bi correspondant ;
- ajouter 1 à b et retrancher simultanément (pour un certain i) ai de bi (autrement dit : on peut ajouter n'importe quels entiers à chacun des rationnels b, b1/a1, ..., br/ar, pourvu que leur somme reste constante) ;
- si la variété n'est pas orientable, remplacer un bi par son opposé ;
- ajouter une fibre de type (1,0).
Toute liste de symboles est équivalente, par ces opérations, à une unique liste normalisée.
Par ailleurs, toute liste est équivalente à une liste (non normalisée) pour laquelle b est nul : il suffit d'ajouter une fibre de type (1, b).
Chaque liste normalisée est un invariant du fibré de Seifert associé, à isomorphisme près (orienté ou pas, selon le type), mais pas de la variété de Seifert à homéomorphisme près. En effet, certaines variétés de Seifert (comme les espaces lenticulaires) peuvent être fibrées de plusieurs façons et correspondre ainsi à plusieurs listes normalisées. En outre, changer l'orientation d'une fibration orientée a pour effet de remplacer b et tous les bi par leurs opposés, ce qui, après normalisation, donne la liste (-b-r,(ε,g);(a1, a1-b1),...,(ar, ar-br)), qui représente la même variété orientable, mais munie de l'orientation inverse.
La somme b + Σbi/ai est un invariant des fibrations orientées. Elle est nulle si et seulement s'il existe un revêtement fini de B sur lequel le fibré induit est trivial.
La caractéristique d'Euler d'orbifold χ(B) de l'orbifold B est donnée par
- χ(B) = χ(B0)−Σ(1−1/ai)
où χ(B0) est la caractéristique d'Euler usuelle de la surface B0 sous-jacente à l'orbifold B. Le comportement de M dépend en grande partie du signe de χ(B).
Groupe fondamental[modifier | modifier le code]
Le groupe fondamental de M s'insère dans la suite exacte
où π1(B) est le groupe fondamental d'orbifold de B (qui diffère du groupe fondamental de sa variété sous-jacente B0). L'image du groupe π1(S1) est un sous-groupe normal cyclique – engendré par l'élément h représenté par n'importe quelle fibre régulière – mais le morphisme de π1(S1) dans π1(M) n'est pas toujours injectif.
Le groupe fondamental de M a la présentation suivante, par générateurs et relations :
- si B est orientable :
où ε vaut 1 pour le type o1, et -1 pour le type o2.
- si B est non orientable :
où εi vaut 1 ou -1 selon que le générateur correspondant vi préserve ou inverse l'orientation de la fibre. (Donc les εi valent tous 1 pour le type n1, tous -1 pour le type n2, seul le premier vaut 1 pour le type n3, et seuls les deux premiers pour le type n4.)
Caractéristique d'Euler d'orbifold strictement positive[modifier | modifier le code]
Les listes normalisées de symboles correspondant à des fibrés de Seifert dont l'orbifold a une caractéristique d'Euler strictement positive sont énumérées ci-dessous. Beaucoup correspondent à différentes fibrations de Seifert d'une même variété. La géométrie de Thurston de la variété correspondante est de type sphérique (en) si le groupe fondamental est fini, et de type S2×R sinon, c'est-à-dire si la variété est non orientable ou si b+Σbi/ai= 0.
(b,(o1, 0);) (b entier) est S2×S1 si b=0, et sinon c'est l'espace lenticulaire L(b,1) (en particulier, (1,(o1, 0);)=L(1,1) est la 3-sphère.)
(b,(o1, 0);(a1, b1)) (b entier) est l'espace lenticulaire L(ba1+b1,a1).
(b,(o1, 0);(a1, b1), (a2, b2)) (b entier) est S2×S1 si ba1a2+a1b2+a2b1 = 0, et sinon c'est l'espace lenticulaire L(ba1a2+a1b2+a2b1, ma2+nb2) où ma1−n(ba1+b1) = 1.
(b,(o1, 0);(2, 1), (2, 1), (n, b3)) (b entier) est la variété prismatique (en) P(m, n) avec m = |(b+1)n + b3| (son groupe fondamental est d'ordre 4mn et son premier groupe d'homologie est d'ordre 4m).
(b,(o1, 0);(2, 1), (3, b2), (3, b3)) (b entier) a pour groupe fondamental une extension centrale du groupe tétraédrique A4 par un groupe cyclique.
(b,(o1, 0);(2, 1), (3, b2), (4, b3)) (b entier) a pour groupe fondamental le produit d'un groupe cyclique d'ordre |12b+6+4b2 + 3b3| et du groupe binaire octaédrique (en) (d'ordre 48), qui est un revêtement double du groupe octaédrique (d'ordre 24).
(b,(o1, 0);(2, 1), (3, b2), (5, b3)) (b entier) a pour groupe fondamental le produit d'un groupe cyclique d'ordre m=|30b+15+10b2 +6b3| et du groupe binaire icosaédrique (en) (d'ordre 120 et parfait), qui est un revêtement double du groupe icosaédrique A5. La variété est le quotient de la sphère de Poincaré par un groupe cyclique d'ordre m. En particulier, (−1,(o1, 0);(2, 1), (3, 1), (5, 1)) est la sphère de Poincaré.
(b,(n1, 1);) (b = 0 ou 1) sont les deux 3-variétés compactes connexes non orientables de géométrie S2×R : pour b = 0 c'est le produit du plan projectif réel par le cercle et pour b = 1 c'est le tore de l'application antipodale de S2.
(b,(n1, 1);(a1, b1)) (b = 0 ou 1) sont les deux mêmes variétés non orientables de géométrie S2×R. Le produit du plan projectif par le cercle correspond aux cas où ba1+b1 est pair.
(b,(n2, 1);) (b entier) est la variété prismatique P(1, |b|), sauf pour b = 0 où c'est la somme connexe de deux copies de l'espace projectif RP3, et pour |b| = 1 où c'est l'espace lenticulaire de groupe fondamental Z/4Z.
(b,(n2, 1);(m, b1)) (b entier) est la variété prismatique P(m, |bm + b1|).
Caractéristique d'Euler d'orbifold nulle[modifier | modifier le code]
Les listes normalisées de symboles correspondant à des fibrés de Seifert dont l'orbifold a une caractéristique d'Euler nulle sont énumérées ci-dessous. La géométrie de Thurston de la variété correspondante est euclidienne si elle est non orientable ou si b+Σbi/ai= 0 – ou, ce qui est équivalent : si son groupe fondamental est virtuellement abélien, c'est-à-dire possède un sous-groupe abélien d'indice fini – et c'est la géométrie Nil (en) sinon. Il y a dans cette liste 10 variétés euclidiennes, mais 4 d'entre elles ont deux fibrations de Seifert différentes. Dans cette liste figurent également tous les fibrés associés à des automorphismes du 2-tore de trace 2, 1, 0, −1 ou −2 (ceux associés aux autres automorphismes – d'Anosov – ne sont pas de Seifert, mais ont une géométrie Sol (en)). Les variétés de géométrie Nil ont une unique fibration de Seifert, et sont caractérisées par leur groupe fondamental.
(b,(o1, 0); (3, b1), (3, b2), (3, b3)) (b entier, bi = 1 ou 2) : dans le cas euclidien b+Σbi/ai= 0, c'est le fibré orienté en 2-tores sur le cercle associé à une rotation d'ordre 3 (de trace −1) du 2-tore.
(b,(o1, 0); (2,1), (4, b2), (4, b3) (b entier, bi = 1 ou 3) : idem en remplaçant ordre 3 (trace -1) par ordre 4 (trace 0).
(b,(o1, 0); (2, 1), (3, b2), (6, b3)) (b entier, b2 = 1 ou 2, b3 = 1 ou 5): idem avec ordre 6 (trace 1).
(b,(o1, 0); (2, 1), (2, 1), (2, 1), (2, 1)) (b entier) : ce sont des fibrés orientés en 2-tores sur le cercle associés à des automorphismes du 2-tore de trace -2. Dans le cas euclidien (b=−2), cet automorphisme est une rotation d'ordre 2 et l'espace est homéomorphe à celui de (0,(n2, 2);).
(b,(o1, 1); ) (b entier) : ce sont des fibrés orientés en 2-tores sur le cercle associés à des automorphismes de trace 2. Dans le cas euclidien (b=0), cet automorphisme est l'identité et l'espace est le 3-tore.
(b,(o2, 1);) (b = 0 ou 1) : ce sont deux fibrés en bouteilles de Klein sur le cercle. Pour b=0 c'est le fibré trivial et le premier groupe d'homologie de la variété est Z+Z+Z/2Z. Pour b=1 c'est le fibré associé à un twist de Dehn (en) de la bouteille et le premier groupe d'homologie est Z+Z. Ces deux variétés (non orientables et euclidiennes) sont homéomorphes à celles des deux fibrés (b,(n1, 2);).
(0,(n1, 1); (2, 1), (2, 1)) : variété (non orientable et euclidienne) de premier groupe d'homologie Z+Z/4Z, homéomorphe à celle du fibré en bouteilles de Klein (1,(n3, 2);).
(b,(n1, 2);) (b = 0 ou 1) : ce sont les deux fibrés (non orientables et euclidiens) en 2-tores sur le cercle associés aux deux involutions sans point fixe qui renversent l'orientation. Ces deux variétés sont homéomorphes à celles des deux fibrés en bouteilles de Klein (b,(o2, 1);).
(b,(n2, 1); (2, 1), (2, 1)) (b entier) : orienté et, si b=−1, euclidien.
(b,(n2, 2); ) (b entier) : orienté. Dans le cas euclidien (b=0), la variété est homéomorphe à celle du fibré en 2-tores (−2,(o1, 0); (2, 1), (2, 1), (2, 1), (2, 1)).
(b,(n3, 2);) (b = 0 ou 1) : ce sont les deux autres fibrés en bouteilles de Klein sur le cercle, associés à l'homéomorphisme y (en) et à son produit par le twist. Pour b=1, l'espace est homéomorphe à celui de (0,(n1, 1); (2, 1), (2, 1)). Pour b=0, le premier groupe d'homologie est Z+Z/2Z+Z/2Z.
Caractéristique d'Euler d'orbifold strictement négative[modifier | modifier le code]
C'est le cas général. Dans ce cas, le fibré de Seifert est déterminé par le groupe fondamental de l'espace. Cet espace est asphérique (i.e. tous ses groupes d'homotopie suivants sont triviaux). Sa géométrie de Thurston est celle du revêtement universel de SL2(R), sauf s'il possède un revêtement fini qui se décompose en un produit (ou, ce qui est équivalent : si la variété est non orientable ou si b+Σbi/ai= 0), auquel cas sa géométrie est celle de H2×R.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- (de) H. Seifert, Topologie dreidimensionalen gefaserter Räume, Acta Math. 60 (1933), 147-238. (Il existe une traduction en anglais par Wolfgang Heil, publiée en 1976 par l'Université d'État de Floride.)
- (en) Ronald Fintushel, Local S1 actions on 3-manifolds (en), Pacific J. o. M. 66 N°1 (1976) 111-118
Références (en anglais)[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Seifert fiber space » (voir la liste des auteurs).
- Matthew Brin, Seifert Fibered Spaces: Notes for a course given in the Spring of 1993, arXiv:0711.1346
- .
- John Hempel, 3-Manifolds, AMS, 2004 (ISBN 978-0-8218-3695-8), aperçu sur Google Livres.
- William Jaco, Lectures on Three-Manifold Topology (ISBN 978-0-8218-1693-6) , aperçu sur Google Livres.
- William Jaco et Peter Shalen, Seifert Fibered Spaces in 3-Manifolds, Memoirs AMS 220, 1979 (ISBN 978-0-8218-2220-3), aperçu sur Google Livres.
- Peter Orlik (de), Seifert Manifolds, Lecture Notes in Mathematics 291, Springer, 1972.
- Frank Raymond, « Classification of the actions of the circle on 3-manifolds », Trans. A.M.S. 31 (1968), 51-87, [lire en ligne].
- G. Peter Scott, « The geometries of 3-manifolds » (errata), Bull. London Math. Soc. 15 (1983), no 5, 401-487.



![{\displaystyle \langle u_{1},v_{1},...u_{g},v_{g},q_{1},...q_{r},h|u_{i}h=h^{\varepsilon }u_{i},v_{i}h=h^{\varepsilon }v_{i},q_{i}h=hq_{i},q_{j}^{a_{j}}h^{b_{j}}=1,q_{1}...q_{r}[u_{1},v_{1}]...[u_{g},v_{g}]=h^{b}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c735c744f6d4264a87ae5fad7d6726a791312472)
