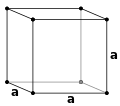
Cubique centré

La structure cubique centrée (cc), dite aussi cubique à corps centré (ccc), est un type de structure cristalline. Elle se rencontre dans tous les métaux alcalins et dans les métaux baryum, radium, vanadium, niobium, tantale, chrome, molybdène, et tungstène, ainsi que le fer à l'état alpha (stable aux températures ordinaires et jusqu'à 912 °C).

Structure[modifier | modifier le code]

Dans cette structure, les atomes sont situés :

aux 8 sommets d'un cube ;
au centre du cube.

L'image ci-dessus indique que l'atome au centre possède huit (8) voisins et alors l'indice de coordination est de 8 (chaque atome au sommet possède aussi huit voisins si on suppose que le dessin continue jusqu'à une distance infinie dans toutes les directions).

Chaque atome dans les coins ne comptant que pour 1/8 (chaque atome est partagé par 8 mailles différents) et l'atome central pour 1, la maille conventionnelle de cette structure comporte 2 atomes. Elle est entièrement déterminée par un unique paramètre de maille, la longueur de l'arête a :

a = b = c ;
α = β = γ = 90°.

Paramètre de maille[modifier | modifier le code]

Dans le cas d'un cristal composé d'un seul type d'atome, on peut utiliser le modèle des sphères dures : les atomes sont considérés comme étant des boules indéformables de rayon R qui sont au contact.

La distance entre deux coins opposés du cube est égale à ${\sqrt {3}}$ fois le paramètre de maille a. Mais, dans le cas d'une structure cubique centrée, cette distance est deux fois le diamètre atomique ou quatre fois le rayon = 4R, de sorte que :

a={\frac {4}{\sqrt {3}}}\cdot R

.

Compacité[modifier | modifier le code]

La compacité, proportion d'espaces occupés par les atomes de la maille cubique centrée est de :

$c={\frac {\mathrm {Volume~occup{\acute {e}}} }{\text{Volume total}}}={\frac {2\times V_{atome}}{a^{3}}}={\frac {2\times ({\frac {4}{3}}\cdot \pi R^{3})}{({\frac {4}{\sqrt {3}}}\cdot R)^{3}}}={\frac {\pi \cdot {\sqrt {3}}}{8}}\simeq 0,68$ .

Cette valeur est inférieure à celles des structures cubique à faces centrées et hexagonale compacte qui sont toutes deux de 0,74. On dit que ces deux dernières correspondent à l'empilement compact ou de compacité maximale, tandis que la structure cubique centrée est une structure non-compacte au sens strict parce que sa compacité n'est pas maximale.

Sites interstitiels[modifier | modifier le code]

Sites tétraédriques dans un empilement Cubique Centré

Situés aux 1/4 et 3/4 des médiatrices des arêtes : 4 sites par face conjointe à 2 mailles : 6 × 4/2 = 12 sites par maille.

Soit au total 12 sites tétraédriques par maille.

Sites octaédriques dans un empilement Cubique Centré
- Centre des faces : 6 faces conjointes à 2 mailles : 6/2 = 3 sites par maille.
- Milieu des arêtes : 12 arêtes conjointes à 4 mailles : 12/4 = 3 sites par maille.

Soit au total 6 sites octaédriques par maille.

Remarque : par une vision géométrique des sites interstitiels, on peut déterminer le rayon $R_{i}$ de l'atome en insertion sans qu'il n'y ait déformation de la maille. On a par exemple pour les sites octaédriques : $R_{i}=0.07a$ , (avec $a$ le paramètre de maille).