Système réticulaire triclinique

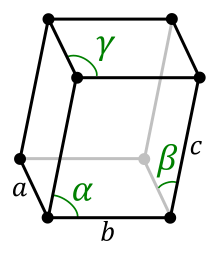
En cristallographie, le système réticulaire triclinique est l'une des sept (dans l'espace à trois dimensions) catégories que l'on utilise pour classer les cristaux sur la base de la symétrie du réseau de Bravais. Dans le système réticulaire triclinique, le réseau de Bravais a la symétrie 1 et est décrit par trois vecteurs de base de longueurs inégales. De plus, les trois vecteurs ne sont pas mutuellement orthogonaux. Le réseau triclinique est le seul réseau de Bravais qui ne possède ni miroirs ni axes de rotation.

Symétrie[modifier | modifier le code]

Les groupes ponctuels de symétrie qui se classent dans ce système réticulaire sont listés ci-dessous, suivis par leur représentation dans la notation internationale (Hermann-Mauguin) et la notation de Schoenflies.

Nom	Internationale	Schoenflies
triclinique hémièdre	1	C₁
triclinique holoèdre	1	C_i (appelé également S₂)

À chaque groupe ponctuel est associé un seul groupe d'espace : P1 et P1. Le seul mode de réseau compatible avec la symétrie triclinique est le mode primitif.

Descriptions non conventionnelles[modifier | modifier le code]

Dans certains cas, la structure des cristaux tricliniques est décrite dans des groupes d'espaces non conventionnels centrés, par exemple C1. Cela permet de comparer plus facilement la structure de cristaux polymorphes (comme pour la cookéite) ou d'étudier l'évolution de la structure d'un cristal lors d'une transition de phase structurelle. Cependant, le mode de réseau du cristal triclinique est toujours primitif.

Dans le cas d'un cristal triclinique décrit dans une maille centrée C, les paramètres $a_{P}$ , $b_{P}$ et $c_{P}$ de la maille primitive sont reliés à ceux de la maille centrée, $a_{C}$ , $b_{C}$ et $c_{C}$ , par :

{\begin{array}{rcl}{\vec {a}}_{C}&=&{\vec {a}}_{P}+{\vec {b}}_{P}\\{\vec {b}}_{C}&=&-{\vec {a}}_{P}+{\vec {a}}_{P}\\{\vec {c}}_{C}&=&{\vec {c}}_{P}\end{array}}

Voir aussi[modifier | modifier le code]

Articles connexes[modifier | modifier le code]