Système réticulaire cubique

En cristallographie, le système réticulaire cubique (ou isométrique) est un système réticulaire dont la maille conventionnelle a la forme d'un cube.

Si la maille conventionnelle de ces cristaux est bien un cube, la maille primitive n'en est pas un quand la maille conventionnelle est centrée ou à faces centrées.

Réseau de Bravais[modifier | modifier le code]

Il existe trois réseaux de Bravais cubiques :

Réseau de Bravais cubique
Nom	cubique primitif	cubique centré	cubique à faces centrées
Symbole de Pearson	cP	cI	cF
Maille élémentaire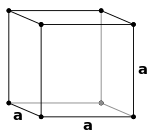

Ces trois réseaux ont les caractéristiques suivantes :

le réseau cubique primitif, ou cubique simple (en abrégé cP^[1]) possède un nœud du réseau à chaque sommet du cube. Chaque nœud du réseau étant partagé par huit cubes adjacents, la maille conventionnelle contient donc au total un nœud du réseau ( $1 / 8$ $\times 8$ ) ;
le réseau cubique centré (en abrégé cI^[1] ou bcc, de l'anglais body-centered cubic) possède un nœud du réseau au centre de la maille en plus des huit situés aux sommets du cube. Il a donc deux nœuds du réseau par maille conventionnelle ( $1 / 8$ $\times 8 + 1$ ) ;
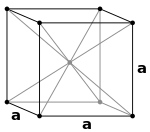
le réseau cubique à faces centrées (en abrégé cF^[1] ou fcc de l'anglais face-centered cubic, également appelé cubique à arrangement compact ou ccp de l'anglais cubic close-packed) possède des nœuds du réseau sur les six faces du cube, qui contribuent chacun pour moitié, en plus des nœuds situés aux sommets, donnant un total de quatre nœuds du réseau par maille conventionnelle ( $1 / 8$ $\times 8$ des sommets plus $1 / 2$ $\times 6$ des faces).

Tout autre type de maille est incompatible avec la symétrie cubique et conduirait à une symétrie inférieure.

Voir aussi[modifier | modifier le code]

Structure cristalline
Système cristallin cubique
Réseau réciproque
Atomium : construction qui représente la maille conventionnelle cubique centrée du fer, avec une diagonale verticale passant par le nœud central

Lectures complémentaires[modifier | modifier le code]

Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., Wiley, (ISBN 0-471-80580-7)

Notes et références[modifier | modifier le code]

↑ ^{a b et c} (en) « International Tables for Crystallography », 2016, section 2.1.1, p. 14–16.

[ITC211-1] {a b et c} (en) « International Tables for Crystallography », 2016, section 2.1.1, p. 14–16.

[1]