Paramètre cristallin
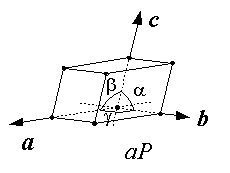
Les paramètres cristallins, aussi appelés paramètres de maille, sont des grandeurs utilisées pour décrire la maille d'un cristal. On distingue trois longueurs (a, b, c) et trois angles (α, β, γ) qui déterminent entièrement le parallélépipède qu'est la maille, élémentaire ou multiple. Les paramètres a, b et c sont mesurés en ångströms (Å), en nanomètres (nm), parfois en picomètres, et α, β et γ en degrés (°).
On utilise aussi l'expression constantes de réseau mais elle est malencontreuse car les paramètres cristallins d'un matériau ne sont pas constants mais varient, en particulier en fonction de la température, de la pression et de la présence de défauts ponctuels.
Paramètres cristallins des systèmes réticulaires
[modifier | modifier le code]Les paramètres de maille d'un cristal sont en général différents les uns des autres. Selon le système réticulaire du cristal, la symétrie du réseau peut imposer certaines égalités entre a, b et c et entre α, β et γ, ou pour ces angles des valeurs précises. Dans les systèmes de faible symétrie les paramètres peuvent prendre n'importe quelle valeur, y compris des valeurs correspondant à une symétrie plus élevée. Ce phénomène de symétrie métrique plus élevée que celle imposée par la symétrie du réseau se manifeste dans un intervalle de température et pression plus ou moins étroit.
| Système réticulaire | Paramètres cristallins |
|---|---|
| triclinique | a, b, c, α, β, γ |
| monoclinique | a, b, c, β, α = γ = 90° |
| orthorhombique | a, b, c, α = β = γ = 90° |
| tétragonal (quadratique) | a = b, c, α = β = γ = 90° |
| rhomboédrique | a = b = c, α = β = γ |
| hexagonal | a = b, c, α = β = 90°, γ = 120° |
| cubique | a = b = c, α = β = γ = 90° |
Détermination des paramètres cristallins
[modifier | modifier le code]
La détermination des paramètres de maille est la première étape pour déterminer la structure d'un cristal. Les méthodes utilisées sont :
- la microscopie à force atomique ;
- le plus souvent, la diffraction de rayons X, de neutrons ou d'électrons.
Dans le cas de la diffraction, les quantités accessibles expérimentalement sont les intensités des réflexions, leurs positions et leurs largeurs de raie.
Pour les mesures sur poudre, on obtient un diffractogramme linéaire, contenant les intensités en fonction de l'angle de diffraction θ. Plusieurs méthodes d'indexation permettent de déterminer directement les paramètres de maille du cristal.
Pour les mesures sur monocristal, à partir des positions des réflexions dans l'espace tridimensionnel, il est possible de déterminer les paramètres de maille et le réseau de Bravais du réseau réciproque ; les paramètres de maille du cristal sont calculés à partir de ceux du réseau réciproque.
Applications en sciences des matériaux
[modifier | modifier le code]Les paramètres cristallins déterminent l'espace vide entre les atomes du réseau, c'est-à-dire la taille des sites interstitiels[1]. Cela joue un rôle important pour la notion de solution solide, et pour comprendre et prédire les transformations que peuvent subir les matériaux lors des variations de température et de pression, comme la transformation martensitique lors de la trempe de l'acier.
Les paramètres de maille évoluent également en fonction du taux de solution solide :
- dans le cas d'une solution par substitution, la maille est dilatée si l'atome étranger est plus gros que l'atome natif, et contractée dans le cas contraire ;
- dans le cas d'une solution interstitielle (par insertion), la maille est toujours dilatée ;
ainsi, on peut relier les paramètres de maille à la concentration d'atomes étrangers, par exemple par la loi de Vegard[2], ou bien par simulation numérique. La mesure des paramètres de maille, typiquement par diffraction de rayonnements (X, neutrons, électrons) permet donc de déterminer le taux de solution.
La comparaison des paramètres cristallins de deux matériaux donne une indication sur leur compatibilité structurelle, pour les précipités (durcissement structural) et pour la croissance hétéro-épitaxiale de couches minces (le fait de faire croître un cristal par-dessus un autre, les cristaux ayant quasiment la même orientation).
Lorsque les paramètres cristallins sont assez proches, la structure cristalline du matériau épitaxié s'adapte à celle du substrat sans grande modification hormis la taille de la maille : c'est l'« adaptation de maille ». La maille de la couche fine est distordue, et l'interface peut présenter des dislocations relaxant ces distorsions[3]. Lorsque les paramètres cristallins sont trop différents, la couche épitaxiée subit des contraintes provoquant des défauts cristallins au sein des couches épitaxiées, pouvant aller jusqu'à l'apparition de fissures.
Dans le cas des semi-conducteurs, l'adaptation de maille permet de changer localement la bande interdite (gap) sans modifier la structure cristalline. Cette particularité rend possible la construction de diodes électroluminescentes et de diodes laser (par exemple les VCSEL).
Ainsi, l'arséniure de gallium, l'arséniure de gallium-aluminium et l'arséniure d'aluminium ont des paramètres de maille très proches : cela rend possible la croissance et l'empilement de couches épitaxiées non contraintes.
Cette comparaison de paramètres de maille entre matériaux permet également d'expliquer la tenue d'une couche d'oxyde protectrice, ou au contraire la dégradation de la couche d'oxyde, dans le cas de la corrosion à haute température des métaux. Lorsqu'un métal s'oxyde, on définit le rapport de Pilling et Bedworth comme étant le rapport entre le volume de l'oxyde et le volume de métal[4]. Si ce rapport est très différent de 1, l'oxydation crée des contraintes importantes menant à la décohésion ou à la rupture de la couche d'oxyde.
Notes et références
[modifier | modifier le code]Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 J. Philibert, A. Vignes, Y. Bréchet et P. Combrade, Métallurgie, du minerai au matériau, Paris, Dunod, , 2e éd., 1177 p. (ISBN 978-2-10-006313-0)
J. Philibert, A. Vignes, Y. Bréchet et P. Combrade, Métallurgie, du minerai au matériau, Paris, Dunod, , 2e éd., 1177 p. (ISBN 978-2-10-006313-0)
Liens externes
[modifier | modifier le code]- Notices dans des dictionnaires ou encyclopédies généralistes :
