Aérodynamique de la pointe avant
La conception aérodynamique de la pointe avant de tout véhicule ou se déplaçant au sein d'un milieu fluide compressible (comme une fusée ou un avion, un missile ou une balle), est un problème important. Ce problème consiste à déterminer la forme de la pointe avant afin d'obtenir la performance optimale. Pour de nombreuses applications, il sera choisi comme pointe avant un solide de révolution minimisant la résistance au mouvement dans un fluide.
Lorsque, par contre, un corps se déplace dans un fluide incompressible (donc à une vitesse assez différente de la vitesse du son, comme par exemple une automobile ou une fusée en subsonique) la forme de sa pointe avant (ou avant-corps), très contre intuitivement, est assez indifférente, pourvu que l'évolution de ses sections soit assez régulière et que son élancement soit assez important (donc que sa forme ne soit pas trop abrupte). (voir plus bas Coefficient de trainée de pointes avant ainsi que l'article Aérodynamique automobile.
Forme de pointe avant et équations[modifier | modifier le code]
Dimensions générales[modifier | modifier le code]
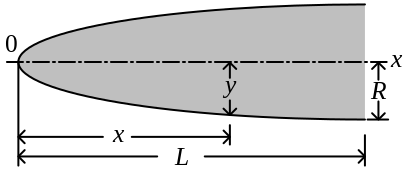
Dans toutes les équations de pointe avant qui vont suivre, L est la longueur totale de la pointe et R est le rayon de la base de la pointe. y est le rayon en tout point x, comme X varie de 0, au bout de la pointe jusqu'à L. Les équations définissent le profil de bidimensionnel de la forme de la pointe avant. La surface de révolution de la pointe est formée par la rotation du profil autour de l'axe (C / L).
Notez que les équations décrivent la forme théorique parfaite ; en pratique elle est souvent émoussée ou tronquée pour des raisons de fabrication ou d'aérodynamique.
Pointe conique[modifier | modifier le code]
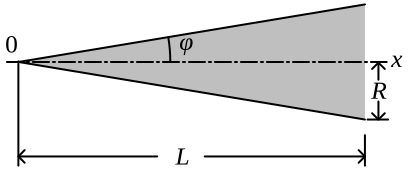
Une forme de pointe avant très commune est le cône. Cette forme est souvent choisie pour sa facilité de fabrication, et est aussi souvent choisie (et parfois mal choisie) pour ses caractéristiques de traînée. Les génératrices d'un cône sont des droites, l'équation du diamètre est tout simplement
Les cônes sont parfois définis par leur demi angle au sommet, :
- and
Pointe conique tronquée par une sphère[modifier | modifier le code]

En pratique, une pointe conique est souvent tronquée par un morceau de sphère. Le point de tangence de la sphère avec le cône se trouve à:
- où:
- et le rayon de la sphérique
Le centre de la sphère troncatrice se trouve à:
Et le point d'apex se trouve à:
Pointe biconique[modifier | modifier le code]
Une pointe biconique est simplement un cône de longueur L1 tronqué par un autre cône de longueur L2.

- L = L1 + L2
- pour :
demi angle :
- and
- pour :
demi angle:
- and
Pointe à ogive tangente[modifier | modifier le code]
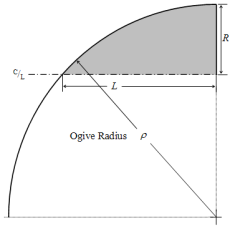
Avec la forme conique, la forme en ogive est la plus familière dans les micro fusées. Ce profil de révolution est obtenu à partir d'un arc de cercle tangent à la base au corps de l'engin (fusée, balle…). La popularité de cette forme est largement due à la facilité de la construction de son profil.
Le rayon de l'arc de cercle qui forme l'ogive est appelé rayon de l'ogive et est lié à la longueur et la largeur de la pointe avant par la formule:
Le rayon y à chaque point x, avec x variant de 0 à L est:
La longueur de la pointe avant, L, doit être inférieure ou égale au rayon de l'ogive ρ. S'ils sont égaux, la forme est un hémisphère.
Pointe à ogive tangente tronquée par une sphère[modifier | modifier le code]

Une forme en ogive est souvent tronquée par un morceau de sphère. Le point de tangence entre la sphère et l'ogive se définit comme suit:
- où:
- est le rayon et est le centre de la sphère troncatrice.
Le point d'apex peut être défini comme suit:
Pointe à ogive sécante[modifier | modifier le code]
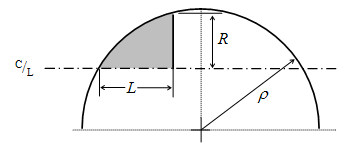
Le profil de cette forme est également formé d'un arc de cercle définit par le rayon de l'ogive. Le corps de l'engin n'est pas tangent à la base de l'ogive. Le rayon de l'ogive ρ n'est pas déterminé par R et L (comme pour l'ogive tangente), mais l'un des facteurs doit être choisi pour définir la forme de la pointe. Si l'on choisit le rayon de l'ogive sécante plus grande que le rayon de l'ogive tangente avec le même R et L, l'ogive sécante résultante apparaitra comme une ogive tangente avec une base tronquée.
- et
Alors le rayon y au point x avec x variant de 0 à L vaut:
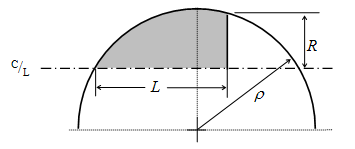
Si on choisit plus petit que le rayon de l'ogive tangente , alors on obtient une ogive sécante qui aura un renflement plus important que le diamètre de la base. L'exemple classique de cette forme est la pointe avant du missile MGR-1 Honest John. De plus, le rayon choisi doit être plus grand que la moitié de la longueur de la pointe avant.
Pointe elliptique[modifier | modifier le code]
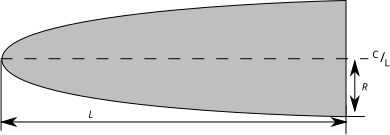
Le profil de cette forme est une moitié d'une ellipse, avec le grand axe dans l'axe et le petit axe étant la base de la pointe avant. Une rotation d'une ellipse complète autour de son axe majeur est un ellipsoïde, ainsi la forme de nez elliptique est un hémiellipsoïde. Cette forme est très utilisée pour le vol subsonique (tels que les fusées miniatures) en raison de l'arrondi de la pointe et de la tangence à la base. Ce n'est pas une forme que l'on retrouve sur les vraies fusées. Si R est égal à L, il s'agit d'un hémisphère.
Pointe parabolique[modifier | modifier le code]
La forme parabolique série est produite par la rotation d'une partie de parabole autour d'une ligne parallèle à son latus rectum. Cette construction est semblable à celle de l'ogive tangente, sauf que la génératrice est un arc de parabole plutôt qu'un arc de cercle. Tout comme sur une ogive, cette construction donne une forme de pointe avant avec un pointe aiguë. Pour la forme émoussée généralement associée à un nez parabolique, voir la série des formes définie par des fonctions puissances (La forme parabolique est également souvent confondue avec la forme elliptique).
Pour :
K’ pouvant varier de 0 à 1, mais les valeurs les plus communes utilisées pour les pointes avant sont:
- K’ = 0 pour un cône
- K’ = 0,5 pour une demi parabole
- K’ = 0,75 pour 3/4 de parabole
- K’ = 1 pour une parabole complète
Dans le cas de la parabole complète (K’=1), la pointe avant est tangente au corps de l'engin à sa base et la base est sur l'axe de la parabole. Les valeurs de K' inférieure à 1 donnent une forme plus affinée qui apparaissent à l'ogive sécante. La forme résultante n'est alors plus tangente à la base de l'engin, mais la base demeure parallèle, bien que décalée, à l'axe de la parabole.
Pointe générée avec une fonction puissance[modifier | modifier le code]
La fonction puissance inclut la forme communément appelée pointe avant « parabolique », mais la véritable pointe avant fait partie des pointes avants générées à partir de fonction parabolique, qui sont complètement différentes des pointes avant générées par des fonctions puissance. La forme générée avec une fonction puissance se caractérise généralement par sa pointe émoussée, et par le fait que sa base n'est pas tangente au corps de l'engin. Il y a toujours une discontinuité de tangence au raccordement de la pointe avant avec le corps de l'engin qui peut être pénalisante pour l'aérodynamique. La forme peut être modifiée à la base pour lisser cette discontinuité. Les formes cylindriques et coniques font partie de cette famille.
Pour :
où:
- n = 1 pour un cône
- n = 0,5 pour une parabole
- n = 0 pour un cylindre
Pointe générée avec une fonction de Haack[modifier | modifier le code]
Contrairement aux formes de pointe avant précédentes, celle obtenu par la fonction de Haack (en) n'est pas construite à partir de bases géométriques. Ces formes proviennent des mathématiques afin de minimiser la traînée aérodynamique. Bien que la fonction de Haack existe pour toute valeur de C, deux valeurs de C ont une importance particulière. Lorsque C = 0, on obtient la traînée minimale pour une longueur et un diamètre donnés (LD-Haack), et lorsque C = 1/3, on obtient la trainée minimum pour une longueur et un volume donnés (LV-Haack). Les pointes avant construites sur les fonctions de Haack ne sont pas parfaitement tangentes, à leur base, au corps de l'engin. La discontinuité de tangente est cependant généralement très faible pour être imperceptible. L'extrémité des pointes avant construites sur les fonctions de Haack ne présentent pas une pointe aigüe mais sont légèrement arrondies.
où:
- C = 1/3 pour LV-Haack
- C = 0 pour LD-Haack
Von Kármán[modifier | modifier le code]
La fonction de Haack donne la traînée minimum pour une longueur et un diamètre donnés (LD-Haack), est communément dénommée Von Kármán ou ogive de Von Kármán.
Aerospike[modifier | modifier le code]
Voir Drag-resistant aerospike (en)
Coefficient de trainée de pointes avant[modifier | modifier le code]

Pour les avions et les fusées, en dessous de Mach 0,8, la trainée de pression sur la pointe avant est négligeable pour toutes les formes (voir le tableau ci-contre, établi pour le subsonique). Le paramètre majeur de la traînée est la traînée de frottement, qui dépend fortement de la surface mouillée, de la régularité de cette surface, et de la présence de discontinuité de la surface. Par exemple, pour les fusées subsoniques, une forme lisse, elliptique, courte et tronquée, est généralement préférable. Dans les régimes transsoniques et au-delà, où la traînée de pression augmente considérablement, la forme de la pointe avant devient très significative. Les facteurs qui influencent la traînée de pression sont la forme générale du cône de nez, son élancement (rapport de sa longueur à son diamètre), et sa régularité.
Influence de la forme générale[modifier | modifier le code]
De nombreuses références sur la conception de pointe avant contiennent des données empiriques comparant les caractéristiques de traînée de différents profils dans les différents régimes. Le graphique présenté ici compile ces données sous forme graphique. Ce tableau corrobore d'autres références plus détaillées, mais plus difficilement compréhensibles telle que celle du USAF Datcom (en).

Dans de nombreuses conceptions de pointe avant, la plus grande préoccupation est la performance dans la plage transsonique de 0,8 à 1,2 Mach. Bien que les données ne sont pas disponibles pour de nombreuses formes dans la région transsonique, le tableau montre clairement que soit la forme de Von Kármán, ou celle obtenue avec la fonction puissance avec n = 1/2, serait préférable aux célèbres pointes avant coniques ou en ogives.
Cette observation va à l'encontre de la sagesse conventionnelle qui prétend que la pointe avant conique est optimale pour passer le mur du son. Les avions de combat sont probablement de bons exemples de pointes avant optimisées pour la région transsonique, bien que leur profil soit souvent déformé par d'autres considérations telles que l'avionique et des prises d'air. Par exemple, la pointe avant des F-16 ressemble fortement à une forme de Von Karman.
Influence de l'élancement de l'ogive[modifier | modifier le code]
Le rapport de la longueur d'une pointe avant par rapport à son diamètre de base est appelé « élancement » (ou parfois abusivement « finesse », sur le modèle anglophone « fineness », mais utiliser le terme « finesse » peut créer une confusion avec la finesse aérodynamique d'un corps, son rapport portance/traînée, bien que cette notion soit inutilisable pour les fusées). La notion d'élancement est souvent appliquée également à l'ensemble de l'engin, en considérant sa longueur totale et son diamètre. On mesure également le rapport longueur / diamètre d'une ogive en calibres (le nombre de calibres est alors son élancement). Aux vitesses supersoniques, l'élancement a un effet significatif sur la traînée d'onde de la pointe avant, en particulier pour les élancements faibles; mais il y a très peu de gain en traînée à attendre d'élancement supérieurs à 5. Avec l'augmentation de l'élancement, en effet, la surface mouillée, et donc la composante de traînée de frottement va augmenter. Par conséquent, l'élancement entrainant la plus faible traînée va être un compromis entre la traînée d'onde et la traînée de frottement (l'une diminuant pendant que l'autre augmente).
Notes et références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Nose cone design » (voir la liste des auteurs).
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) SS. Chin, Missile Configuration Design, New York, McGraw-Hill Publishing Co., (lire en ligne) [PDF]
Liens externes[modifier | modifier le code]
- (en) The Descriptive Geometry of Nose Cones - Gary A. Crowell Sr., Scribd, 1996
- (en) Design of Aerodynamically Stabilized Free Rockets - U.S. Department of Defense, (sur Ebah.com)




































