Limite d'une suite
En mathématiques, de manière intuitive, la limite d'une suite est l'élément dont les termes de la suite se rapprochent quand les indices deviennent très grands. Cette définition intuitive n'est guère exploitable car il faudrait pouvoir définir le sens de « se rapprocher ». Cette notion sous-entend l'existence d'une distance (induite par la valeur absolue dans ℝ, par le module dans ℂ, par la norme dans un espace vectoriel normé) mais on verra que l'on peut même s'en passer pourvu qu'on ait une topologie. Dans cet article seront présentées d'abord la notion de limite de suite réelle, puis celle de suite complexe et seulement après, quitte à être redondant, celle de limite dans un espace topologique.
Histoire[modifier | modifier le code]
Si la formalisation de la limite d'une suite vient assez tard, son utilisation intuitive date de plus de 2 000 ans. Dans les Éléments d'Euclide (X.1), on peut lire : « Étant données deux grandeurs inégales, si, de la plus grande on retranche plus que la moitié, et que du reste on retranche plus que la moitié et si l'on continue toujours ainsi, nous aboutirons à une grandeur inférieure à la plus petite des grandeurs donnée ». En langage actuel, cela donnerait :
- soit (on notera simplement u) une suite de réels positifs telle que, pour tout n, un + 1 < un2, alors, pour tout réel strictement positif e, il existe un indice n tel que un < e.
Cette définition est proche de la définition moderne d'une suite ayant pour limite 0. Si on pourrait croire que cette interprétation du dixième élément d'Euclide est une modernisation fallacieuse, on peut s'assurer que cette affirmation est fausse en regardant l'utilisation qu'en fait Archimède dans ses méthodes de quadrature. Cherchant à calculer l'aire du disque ou l'aire sous une parabole, par exemple, il cherche à l'approcher par des aires de polygones et observe alors la différence entre l'aire cherchée et l'aire du polygone. Il démontre qu'à chaque étape, cette différence a été réduite de plus de la moitié et c'est ainsi qu'il conclut qu'en continuant indéfiniment le processus on sera aussi proche qu'on le souhaite de l'aire cherchée. C'est la « méthode d'exhaustion ».
Cette intuition de la limite mal formalisée ne permettra cependant pas de lever les paradoxes de Zénon, comme celui d'Achille et de la tortue :
- Achille part avec un handicap A et court deux fois plus vite que la tortue. Quand il arrive au point de départ de la tortue, celle-ci a déjà parcouru la distance A/2, Achille parcourt alors la distance A/2 mais la tortue a parcouru la distance A/4 ; à ce train-là, Achille ne rattrape la tortue qu'au bout d'un nombre infini de processus c'est-à-dire jamais.
Il faut attendre ensuite 1 600 ans et les travaux de Grégoire de Saint-Vincent pour entrevoir une tentative de formalisation imparfaite, puis le calcul infinitésimal de Newton et Leibniz.
Limite d'une suite réelle[modifier | modifier le code]
Suite convergente[modifier | modifier le code]
On dit qu'une suite réelle admet pour limite un réel ℓ si :
- tout intervalle ouvert qui contient ℓ contient aussi tous les termes de la suite sauf un nombre fini d'entre eux (c.-à-d. contient tous les termes de la suite à partir d'un certain rang).
On dit également qu'elle converge vers ℓ. Si une suite possède une limite réelle, on dit qu'elle est convergente[1] ou qu'elle converge.
La définition précédente se traduit formellement par :
- [2].
On écrit alors
- ou plus simplement, quand il n'y a pas ambiguïté, , ou encore .
De cette définition, on peut déduire que
- quand elle existe, la limite est unique (car les termes de la suite ne peuvent pas se trouver dans deux intervalles disjoints) ;
- toute suite convergente est bornée ;
- une suite encadrée par deux suites convergeant vers la même limite ℓ converge aussi vers ℓ : c'est le théorème des gendarmes.
Les propriétés de complétude de ℝ permettent aussi d'affirmer que
- toute suite monotone bornée est convergente ;
- toute suite de Cauchy est convergente ;
- deux suites adjacentes convergent et ont la même limite.
Exemples de suites convergentes
- La suite définie par converge vers 0 ; on note donc .
- Si alors la suite converge vers 0.
- Si alors la suite (somme des termes de la suite géométrique de raison q) converge vers .
On dit qu'une suite réelle diverge si elle ne converge pas[1]. Une suite divergente peut soit avoir une limite infinie, soit n'avoir aucune limite.
Limite infinie[modifier | modifier le code]
On dit qu'une suite tend vers +∞ si tout intervalle de la forme ]A, +∞[ contient tous les termes de la suite sauf un nombre fini d'entre eux (c.-à-d. contient tous les termes de la suite à partir d'un certain rang).
Cette définition se traduit formellement par :
- .
On écrit alors
- ou plus simplement, quand il n'y a pas ambiguïté, ou .
On dit qu'une suite tend vers –∞ si tout intervalle de la forme ]–∞, A[ contient tous les termes de la suite sauf un nombre fini d'entre eux.
Cette définition se traduit formellement par :
- .
On écrit alors
- ou plus simplement, quand il n'y a pas ambiguïté ou .
L'exemple fondamental d'une suite tendant vers l'infini est celui de l'inverse d'une suite de signe constant et tendant vers 0 :
- s'il existe N tel que, pour tout n > N, et si alors ;
- s'il existe N tel que, pour tout n > N, et si alors .
Deux résultats sont assez faciles à obtenir :
- toute suite croissante non majorée tend vers +∞ et toute suite décroissante non minorée tend vers –∞ ;
- toute suite supérieure à une suite tendant vers +∞ tend vers +∞ et toute suite inférieure à une suite tendant vers –∞ tend vers –∞.
Exemples de suites n'admettant pas de limite[modifier | modifier le code]
Certaines suites réelles ne tendent ni vers un réel, ni vers +∞, ni vers –∞. C'est le cas, par exemple :
- des suites géométriques de raison inférieure ou égale à –1, comme
- la suite non bornée (1, –2, 4, –8, 16, –32, …), géométrique de raison –2, ou même
- la suite bornée (1, –1, 1, –1, 1, –1, …), géométrique de raison –1 ;
- d'un certain nombre de suites logistiques au comportement chaotique.
Opérations sur les limites[modifier | modifier le code]
On démontre que les opérations sur les suites convergentes se transmettent à leurs limites pour peu que l'opération ait un sens. Cela signifie que si et si alors :
- ;
- ;
- si , on a .
De plus, si f est une fonction continue en et si pour tout , est défini, alors .
L'intervention de suites tendant vers ±∞ rend les calculs un peu plus compliqués :
- Somme :
- si une suite converge et l'autre tend vers l'infini, la somme a même limite que la suite tendant vers l'infini ;
- si les deux suites tendent vers le même infini, il en est de même de leur somme ;
- si les deux suites tendent vers deux infinis différents, on ne peut pas conclure directement ; on dit alors que l'on a une forme indéterminée.
- Produit : on pourra, à condition qu'une limite existe, appliquer la règle des signes ;
- si une suite converge vers un réel non nul et l'autre tend vers l'infini, le produit tendra vers un infini dont le signe se détermine par la règle des signes ;
- si les deux suites tendent vers l'infini, il en sera de même de leur produit ;
- si l'une des suites tend vers 0 et l'autre vers l'infini, on ne peut pas conclure directement ; c'est une seconde forme indéterminée.
- Inverse :
- si une suite tend vers l'infini alors son inverse converge vers 0 ;
- si une suite, de signe constant, converge vers 0 alors son inverse tend vers l'infini
Limite d'une suite complexe[modifier | modifier le code]
On dit qu'une suite converge vers un complexe ℓ si
- .
On remarque qu'il s'agit de la même définition que dans ℝ, au détail près qu'il ne s'agit plus de valeur absolue mais de module.
On écrit alors
- ou plus simplement, quand il n'y a pas ambiguïté, .
On retrouve pour les suites complexes convergentes, les mêmes propriétés que pour les suites réelles, exceptées celles liées à la relation d'ordre : la limite est unique, une suite convergente est de module borné, toute suite de Cauchy converge (en effet, ℂ est aussi complet), les différentes opérations comme somme, produit, quotient se transmettent bien à la limite.
Autres espaces[modifier | modifier le code]
Espace vectoriel normé[modifier | modifier le code]
Dans un espace vectoriel normé, on dit qu'une suite converge vers ℓ si
- .
C'est une généralisation de la limite d'une suite complexe, la norme usuelle dans le plan complexe étant le module.
On écrit alors
- ou plus simplement, quand il n'y a pas ambiguïté, .
L'unicité de la limite est conservée ainsi que la transmission à la limite de la somme et de la multiplication par un scalaire. Ce n'est que dans un espace vectoriel normé complet que l'on pourra affirmer que toute suite de Cauchy converge.
Espace métrique[modifier | modifier le code]
Dans un espace métrique, on dit qu'une suite converge vers ℓ si
- .
On remarque qu'il s'agit de la même définition que dans , au détail près qu'il ne s'agit plus de valeur absolue d'une différence mais de distance.
On écrit alors
- ou plus simplement, quand il n'y a pas ambiguïté, .
Seule l'unicité de la limite est conservée. Il faudra être dans un espace métrique complet pour pouvoir dire que toute suite de Cauchy converge. Si une opération existe sur l'espace en question, il faudra qu'elle soit continue pour se transmettre à la limite.
Espace topologique[modifier | modifier le code]
Toutes les définitions précédentes se rejoignent dans la définition de la convergence dans un espace topologique.
Soit E un espace muni d'une topologie T.
On dit que la suite converge vers si, pour tout ouvert O de T contenant l'élément ℓ, il existe un entier naturel N tel que tous les pour appartiennent à O.
Il suffit que l'espace soit séparé pour pouvoir affirmer que la limite est unique.
Valeurs d'adhérence[modifier | modifier le code]
Cette section ne traite que le cas des suites à valeurs dans un espace métrique donc à bases dénombrables de voisinages. Dans ce cadre, la notion de valeur d'adhérence telle que définie ci-dessous coïncide avec la notion générale, qui est différente.
Définitions[modifier | modifier le code]
Soit une suite à valeurs dans un espace métrique E.
Si est une fonction strictement croissante (une telle fonction s'appelle une extractrice), on dit que la suite est une suite extraite (ou sous-suite) de la suite .
Grosso modo, c'est la suite pour laquelle on n'a gardé que certains termes (une infinité quand même).
On dit que la valeur ℓ est une valeur d'adhérence de la suite s’il existe une suite extraite de qui converge vers ℓ.
Pour se faire une idée, une valeur d'adhérence est un élément « près duquel la suite passe souvent », c'est-à-dire qu'aussi loin qu'on aille, on trouvera toujours un terme de la suite près de cet élément.
Propriétés[modifier | modifier le code]
Propriété 1
Si une suite à valeurs dans E converge vers , est l'unique valeur d'adhérence de c'est-à-dire que toutes les suites extraites convergent vers .
Dans le cas où E est un espace compact, on dispose même d'une réciproque. Elle s'applique par exemple à toute suite à valeurs dans un segment de ℝ (autrement dit à toute suite réelle bornée), ou encore à toute suite réelle, en prenant comme compact la droite réelle achevée (dans ce cas, +∞ et –∞ ne sont pas exclus a priori de l'inventaire des valeurs d'adhérence de la suite) :
Propriété 2
Si une suite est à valeurs dans un espace compact E, alors elle admet au moins une valeur d'adhérence dans E, et elle converge si et seulement si elle n'en admet qu'une.
Propriété 3
Une suite à valeurs dans E converge vers si et seulement si :
- converge vers l et
- converge vers l.
On voit d'ailleurs bien comment généraliser ce résultat[3] : il suffit que les images des extractrices considérées recouvrent entièrement ℕ (par exemple, ici, et ), c'est-à-dire que les ensembles (infinis) d'indices des suites extraites utilisées aient pour réunion l'ensemble des naturels.
Remarque
Cette propriété est utile pour démontrer la non-convergence d'une suite à valeurs dans E : si
- converge vers l1 et
- converge vers l2 avec l1 ≠ l2,
alors ne converge pas.
Exemple
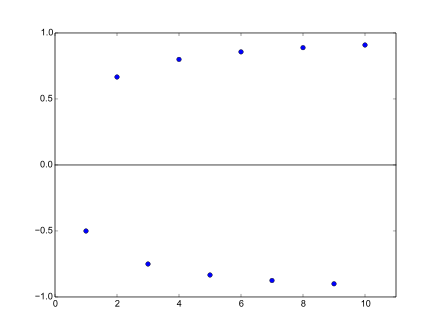
La suite (–12, 23, –34, 45, –56, …) = (cf. figure) est décomposable en deux sous-suites :
- (–12, –34, –56, …) converge vers –1 ;
- (23, 45, …) converge vers 1.
Les deux sous-suites convergeant vers des limites différentes, la suite initiale ne converge pas.
Théorème de Bolzano-Weierstrass[modifier | modifier le code]
Toujours lorsque E est un espace métrique, on dispose du puissant théorème de Bolzano-Weierstrass :
Un espace métrique E est compact si (et seulement si) il est séquentiellement compact, c'est-à-dire si toute suite à valeurs dans E admet au moins une valeur d'adhérence dans E.
Notes et références[modifier | modifier le code]
- Pierre-Henry Terracher et Robert Ferachoglou, Maths - Term S, Hachette Éducation, coll. « Terracher », , p. 13.
- Les formulations obtenues en remplaçant par ou par sont équivalentes à celle-ci, par la même technique que dans « Limite (mathématiques élémentaires) ».
- Cette propriété, démontrée dans un exercice corrigé sur Wikiversité, est utilisée par exemple pour déduire un corollaire d'un théorème de point fixe.



























































