Quadrature de la parabole

La quadrature de la parabole est le calcul de l'aire d'un segment de parabole, surface délimitée par une parabole et une droite. Les premières techniques de quadrature sont développées par Archimède dans son traité La Quadrature de la parabole, l'une est mécanique et l'autre géométrique et utilisent toutes deux une méthode d'exhaustion. On considère qu'il s'agit d'un des premiers calculs d'intégration en mathématiques. D'autres techniques sont développées au IXe siècle et XIe siècle dans les mathématiques arabes. Au XVIIe siècle enfin, on voit apparaître des méthodes générales de quadrature de fonctions puissances avant que le calcul différentiel et intégral ne permette une résolution du problème en quelques lignes.
Calcul d'Archimède par la méthode d'exhaustion[modifier | modifier le code]
Méthode géométrique[modifier | modifier le code]
Principe[modifier | modifier le code]
En mathématiques grecques, les calculs d'aire se font essentiellement par approximation au moyen d'une méthode dite d'exhaustion, reposant sur un double raisonnement par l'absurde. On approche la surface du segment de parabole par des triangles intérieurs à la parabole, cette approximation pouvant être rendue aussi précise que l'on veut.
Développement[modifier | modifier le code]
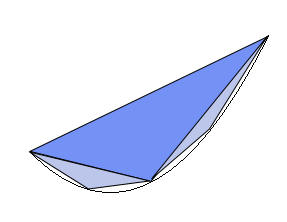
Archimède cherche à calculer l'aire P d'un segment de parabole, c'est-à-dire du triangle curviligne entre les points d'abscisse a et d'abscisse b, l'axe de la parabole étant l'axe vertical. Il dessine alors un triangle passant par les points d'abscisse a, d'abscisse b et d'abscisse . Il décide donc d'approcher P par l'aire S de ce grand triangle. Puis il recommence dans les petits triangles curvilignes laissés pour compte.
Il démontre que l'aire de chaque petit triangle est égal au huitième de l'aire du grand triangle, en démontrant que la distance horizontale a été divisée par deux, tandis que la hauteur a été divisée par 4. Il peut alors approcher P par l'aire du grand triangle et des deux petits : , puis, continuant ainsi, il approche l'aire de la parabole par .
- .
On sait, dès cette époque, que peut s'écrire
mais on ne sait pas passer à la limite. On sait seulement utiliser le principe d'exhaustion qu'Archimède invoque ainsi.
Théorème — Ceci démontré, il est évident qu'il est possible d'inscrire dans ce segment [de parabole] un polygone tel que les segments restants soient inférieurs à toute aire donnée ; car en retranchant toujours une aire qui, en vertu de cette proposition, est supérieure à la moitié [du segment], il est évident qu'en continuant ainsi à diminuer les segments restants [il arrivera un moment où] nous les rendrons inférieurs à toute aire donnée[1].
Ce principe se retrouve dans la proposition 1 du livre X des Éléments d'Euclide et repose sur l'axiome d'Archimède.
Archimède démontre alors qu'il est absurde que P soit plus grande que et que P soit plus petite que .
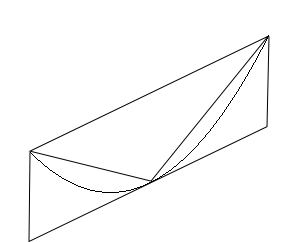
- Supposons que P soit plus grande que .
- Il démontre que la différence entre P et peut être rendue aussi petite que l'on souhaite. En effet, à l'aire de la parabole, on retranche l'aire du triangle qui représente plus de la moitié de l'aire de la parabole car l'aire du triangle vaut exactement la moitié de l'aire du parallélogramme dessiné, aire plus grande que l'aire de la parabole. Et ainsi de suite à chaque étape. Il peut donc rendre plus petite que . Ceci voudrait dire que est plus grande que . C'est absurde d'après l'expression de .
- Supposons que P soit plus petite que .
- Selon le même principe d'exhaustion, on peut rendre la différence aussi petite que l'on veut, puisqu'à chaque étape on retranche les 3/4 de ce qui reste. On pourrait donc la prendre plus petite que . Ceci voudrait dire que est plus grande que P. C'est absurde puisque les triangles sont intérieurs au segment de parabole.
Les deux cas étant éliminés, Archimède conclut que .
Il est intéressant de voir que l'expression « inférieur à toute aire donnée » est très proche de la notion de limite qu'Archimède n'utilise pas. Il se contraint donc de raisonner par l'absurde pour prouver son égalité.
La méthode sera reprise par le mathématicien de langue arabe Ibrahim ibn Sinan[2] qui démontre la propriété en trois étapes. Dans un premier temps, il démontre qu'une affinité conserve les rapports d'aires de polygones. Vient ensuite le cœur de sa démonstration qui applique la méthode d'exhaustion pour prouver que le rapport des aires de deux portions de paraboles est égal au rapport des aires de leur triangles associés. La fin du raisonnement est alors très rapide : dessinant une parabole et son triangle associé, il remarque que l'aire de la parabole est égale à l'aire du triangle associé à laquelle on ajoute les deux aires des portions de paraboles restantes. Il démontre que les triangles associés à ces portions de paraboles ont pour aire 1/8 de l'aire du premier triangle. Il en déduit qu'il en est de même pour le rapport des aires des portions de paraboles et obtient ainsi
- .
Soit encore : .
Méthode des pesées[modifier | modifier le code]
Archimède propose dans le même ouvrage une présentation par pesée de la quadrature qui démontre son génie mécanique. Le principe en est détaillé dans un unique manuscrit du texte d'Archimède, découvert dans un palimpseste en 1906. Dans son traité La Quadrature de la parabole, il complète son raisonnement par l'utilisation de la méthode d'exhaustion.
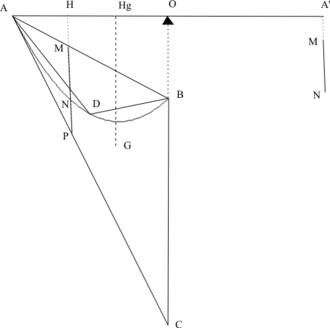
Il décide de peser la parabole par un système de levier.
La figure présentée ici est une simplification de celle figurant dans l'ouvrage d'Archimède. La droite (AC) est tangente en A à la parabole, le segment [BC] est parallèle à l'axe de la parabole. Le point D se projette, parallèlement à l'axe de la parabole, sur le milieu de [AB].
L'idée est d'équilibrer le triangle ABC, suspendu en son centre de gravité G par une masse placée en A'.
Archimède procède par segment. Le triangle ABC suspendu en Hg peut être remplacé par une multitude de segments MP suspendus en H. Archimède a déjà démontré (traité sur les paraboles) que MN est à MP ce que BM est à BA. On dirait maintenant :
- . (1)
Grâce au théorème de Thalès, on a aussi l'égalité
- (2)
Donc
Puis :
Le segment [MN] placé en A' équilibre donc le segment [MP] placé en H.
Segment par segment, il équilibre donc le triangle ABC placé en Hg par la portion de parabole placée en A' . Donc
- Aire de la parabole OA' = Aire du triangle OHg.
Comme , on a
- Aire de la parabole = aire de ABC.
Enfin, dans le même traité sur les paraboles, Archimède a déjà démontré que l'aire de ABC vaut 4 fois l'aire de ABD.
L'aire de la parabole vaut donc de l'aire du triangle ABD.
Utilisation de la formule de la somme des carrés des entiers consécutifs[modifier | modifier le code]

Cette méthode consiste à utiliser les sommes des puissances des entiers consécutifs pour quarrer toutes les « variétés de paraboles »[note 1]. Elle consiste à découper dans la portion de la parabole ou dans la surface sous la parabole des rectangles ou des trapèzes dont l'aire est proportionnelle au carré des entiers. Cette méthode est développée par Blaise Pascal dans son Potestam numericarum Summa (1654) qui utilise la méthode des indivisibles[3] puis par John Wallis en 1656 qui l'étend également à tout exposant rationnel positif dans son Arithmetica infinitorum[4],[5].
Pascal et Wallis calculent l'aire sous la parabole sur l'intervalle [0, a]. L'aire de la portion de parabole peut se déterminer alors par complémentarité.
Pour calculer l'aire sous la parabole entre les points d'abscisse 0 et a, on découpe l'intervalle [0, a] en n intervalles de même taille d, mettant ainsi en évidence les abscisses . Sur l'intervalle l'aire sous la parabole est comprise entre l'aire des rectangles de base d et de hauteurs et [note 2].

Par sommation on arrive à l'inégalité:
soit encore
La formule sur la somme des carrés consécutifs
et un passage à la limite permet de conclure.

Une méthode analogue avait déjà été mise en place au cours du IXe siècle par Thābit ibn Qurra qui, semble-t-il, ne connaissait pas le traité d'Archimède et a été ainsi contraint de développer ses propres méthodes[6]. Thābit ibn Qurra glisse dans sa portion de parabole des trapèzes dont les hauteurs ne sont pas fixes mais construites de telle sorte que les aires des trapèzes soient proportionnelles aux carrés des entiers impairs[7]. Sa méthode consiste à découper, dans la portion de parabole d'équation , pour y compris entre 0 et b, des trapèzes dont les bases ont pour ordonnées . Les trapèzes ainsi créés ont pour hauteur
et pour bases
- et
L'aire de la portion de parabole est donc approchée par la somme des aires des trapèzes, c'est-à-dire par
Par une méthode d'exhaustion (aujourd'hui on passerait à la limite) il prouve alors que l'aire de la portion de parabole vaut les 4/3 de l'aire du triangle associé.
Utilisation de suites géométriques[modifier | modifier le code]
Cette méthode est mise en place par Fermat dès 1636 puis généralisée ensuite pour calculer l'aire sous ce qu'il appelle des paraboles et hyperboles et qui sont en fait les courbes des fonctions puissances (entières, positives, négatives ou 1/n, différentes de –1)[8]. Le principe consiste à découper l'intervalle sous la surface à quarrer selon une progression géométrique. On approche alors l'aire sous la courbe par l'aire des rectangles obtenus par ce découpage; ces aires sont également en progression géométrique. Par un double passage à la limite (limite de la série géométrique, puis limite quand la raison de la suite s'approche de 1), on retrouve l'aire de la surface cherchée.

On peut l'illustrer, dans les notations actuelles, sur la demi-parabole d'équation sur l'intervalle [0,a][note 3] : le découpage de l'intervalle [0,a] selon une progression géométrique de raison r met en évidence les abscisses . Sur l'intervalle l'aire sous la courbe est comprise entre l'aire des rectangles de base
et de hauteurs
- .
Par sommation on arrive à l'inégalité
où est l'aire sous la parabole sur l'intervalle . Par passage à la limite dans la série géométrique de raison , on obtient l'encadrement
puis par simplification par
Un second passage à la limite, pour r tendant vers 1, donne l'égalité
L'aire du demi-segment de parabole est égale au 2/3 du rectangle qui le contient.
Cette technique se généralise à toute courbe d'équation , avec α réel différent de -1, pour calculer l'aire sous la courbe sur [0,a] si α > -1 ou l'aire sous la courbe sur [a; +∞[ si α < -1
Calcul intégral[modifier | modifier le code]
L'aire sous la parabole sur l'intervalle [0, a] correspond à l'intégrale
Le théorème fondamental de l'analyse permet de lier cette intégrale à une primitive F de la fonction carré
Une table de primitives permet de déterminer une primitive de la fonction carré : et fournit le résultat attendu.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- C'est-à-dire toutes les courbes d'équation y = kxn.
- Pascal et Wallis utilisent eux la méthode des indivisibles qui consiste à travailler sur des lignes également espacées et pas des rectangles.
- Ce même exemple est également traité par Fermat mais avec un vocabulaire très éloigné de celui du XXe siècle, voir Pierre de Fermat, Jules Tannery et Charles Henry, Œuvres de Fermat, vol. 3, (lire en ligne), p. 216 et suivantes.
Références[modifier | modifier le code]
- (fr + grc) Archimède, La quadrature de la parabole, Paris, Les Belles Lettres, (ISBN 2-251-00025-9), page 189.
- Rushdī Rāshid et Hélène Bellosta, Ibrāhīm Ibn Sinān, logique et géométrie au Xe siècle, Brill, (lire en ligne), p. 229-244.
- Jean-Louis Gardies, Pascal entre Eudoxe et Cantor (lire en ligne), p. 62.
- (en) Jacqueline Stedall, « The discovery of wonders: reading between the lines of John Wallis's Arithmetica infinitorum », Arch. Hist. Exact Sci., vol. 56, no 1, , p. 1-28 (DOI 10.1007/s004070100040).
- (en) John Wallis, Arithmetica infinitorum, propositions XIX à XXIV.
- (en) Rushdī Rāshid et Régis Morelon, Encyclopedia of the History of Arabic Science, vol. 2, Routledge, (lire en ligne), p. 421.
- Stoll 1993, p. 55.
- Dahan et Peiffer, p. 182.
Bibliographie[modifier | modifier le code]
- A. Dahan-Dalmedico et J. Peiffer, Une histoire des mathématiques : Routes et dédales, [détail des éditions]
- Roshdi Rashed, Les mathématiques infinitésimales du IXe au XIe siècle, vol. 1, Londres, Al-Furqan Islamic Heritage Foundation,
- André Stoll, « Comment l'histoire des mathématiques peut nous dévoiler une approche possible du calcul intégral », Repères-IREM, no 11, (lire en ligne)
- La démonstration mathématique dans l'histoire, IREM de Lyon
- [PDF] Quadrature de la parabole
- [PDF] Quadrature par la méthode des pesées, séminaire de mathématiques, IUFM de La Réunion



























![{\displaystyle [x_{k,n},x_{k+1,n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27de466f4e32bb52188c044755c28bc28e63d31e)















![{\displaystyle [x_{k+1,r},x_{k,r}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe481938f117ef480943ce4a280c0c7b2abc0808)





![{\displaystyle [x_{n,r},a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972477412572b0a8d52e6c37ede5d0e3273921ec)








