Adaptation d'impédances

L’adaptation d'impédances est une technique utilisée en électricité permettant d'optimiser le transfert d'une puissance électrique entre un émetteur (source) et un récepteur électrique (charge)[1] et d'optimiser la transmission des signaux de télécommunications.
- la théorie de la puissance maximale détermine que l'impédance de la charge doit être le complexe conjugué de l'impédance du générateur ;
- dans les lignes de transmission, l'impédance caractéristique est une sorte de perméabilité du milieu qui cause des réflexions quand elle change (comme en optique ou en acoustique) et qui deviennent gênantes quand la longueur de la ligne approche une fraction non négligeable de la longueur d'onde du signal. Elle a la valeur de l'impédance qu'on mesurerait aux bornes d'une ligne de longueur infinie. À la fin d'une ligne de transmission l'impédance du récepteur doit être égale à l'impédance caractéristique de celle-ci pour éviter les réflexions en simulant une prolongation infinie à celle-ci.
Ceci est valable uniquement si l'impédance de l'émetteur est également égale à l'impédance caractéristique de la ligne.
Généralités[modifier | modifier le code]
Dans certains domaines, l'adaptation d'impédance est indispensable, par exemple dans certains systèmes de transmission de l'information ou de transmission radioélectrique. Ce sont généralement les systèmes mettant en jeu les lignes de transmission. Cependant, dans d'autres cas, l'adaptation d'impédance peut être inutile ou nuisible. La raison est que quand les impédances sont adaptées, la puissance dissipée dans la charge est égale à la puissance dissipée dans la résistance interne de la source. L'adaptation donne un rendement énergétique maximal de 50 %. Si l'on veut un bon rendement énergétique il faut que l'impédance de la source soit négligeable par rapport à celle de la charge.
Histoire[modifier | modifier le code]
Le principe de maximisation du transfert de puissance électrique a été évoqué par Moritz von Jacobi en 1837-1839. Ce principe a été à ses débuts mal interprété, en déduisant qu'un moteur électrique alimenté par une batterie ne pourrait être plus efficace que 50 %, car l'énergie perdue dans la batterie serait au moins aussi importante que celle délivrée au moteur[2]. En 1880, cette interprétation est contestée par Edison et son collègue Francis Robin Upton, qui réalisent que le rendement maximal est différent du transfert de puissance maximale. Pour atteindre le rendement maximal, la résistance de la source (batterie ou dynamo) devrait être minimale. Avec ce constat, ils obtiennent une efficacité de 90 %, et prouvent que le moteur électrique peut être une alternative aux machines thermiques.
L'adaptation d'impédance des lignes de transmission est quant à elle issue de l'industrie téléphonique, pour réduire les échos dans les fréquences audibles. La compagnie Bell semble avoir été à l'origine des études d'adaptation d'impédance. L'autotransformateur à impédance adaptée a été inventé par Emil Berliner[3] et breveté le en tant que système Bell-Berliner[4].
Les travaux de Oliver Heaviside, mis en application par Mihajlo Pupin vers 1896, sur l'utilisation de bobines de charge pour adapter les longues lignes de transmission ont réellement lancé les études sur les adaptations d'impédance.
Optimisation du rendement[modifier | modifier le code]

La puissance transférée entre une source électrique et une charge électrique dépend de la tension de la source et des impédances de la source comme de la charge. Le rendement électrique du système est le rapport entre la puissance fournie à la charge (dissipée dans ) et la puissance totale délivrée par la source (dissipée par et ) et il s'écrit :
On peut considérer trois cas remarquables :
- si , alors ;
- si , alors ;
- si , alors .
Le rendement sera donc optimisé si l'impédance de la charge est très grande par rapport à celle de la source, donc désadaptée.
L'adaptation entre quadripôles électriques n'est donc pas toujours désirée. Par exemple, de nombreux quadripôles nécessitent d'être chargés par une résistance grande par rapport à leur résistance de sortie. C'est le cas de filtres avec amplificateurs opérationnels. C'est aussi le cas de filtres LC, pour lesquels les réjections hors bandes sont justement dues au fait qu'il n'y a pas d'adaptation sur les fréquences hors bande passante. C'est aussi le cas en distribution d'énergie électrique.
L'adaptation sera recherchée lorsqu'on veut maximiser le gain ou conserver les caractéristiques d'un quadripôle, si le constructeur a caractérisé ce dernier sous condition d'adaptation.
Optimisation du transfert d'énergie (théorie de la puissance maximale)[modifier | modifier le code]

Pour maximiser la puissance transférée (c'est-à-dire la puissance dans la charge) il faut adapter les impédances. Pour réaliser cette adaptation, on commence par compenser la partie réactive de l'impédance de la source. Il faut, pour cela que :
- .
Puis, il faut que la partie résistive de l'impédance de la charge soit égale à la partie résistive de l'impédance de la source :
- .
En langage mathématique, les deux impédances sont conjuguées. Dans ce cas, la puissance dissipée dans la résistance de charge est :
Il faut remarquer que la même puissance est alors dissipée dans la résistance de la source (le rendement est de 50%).
En notation complexe, le module du courant parcourant le circuit est :
Avec =
=
La puissance moyenne dissipée par la charge s'écrit :
On peut calculer les valeurs de et (avec , , et fixés) pour lesquelles l'expression est un maximum, c’est-à-dire lorsque
est maximal. Le terme des réactances peut facilement être minimisé :
L'équation se simplifie en :
Nous pouvons calculer la valeur de pour laquelle le dénominateur
est minimal.
ou
car les résistances sont positives. La seconde dérivation
est positive pour des valeurs de et positives, donc le dénominateur a un minimum, et est un maximum, lorsque
En conclusion on a
qui peuvent être écrits comme complexes conjugués :

En rouge : rendement du système.
Dans la figure de droite est représentée la puissance relative transférée à la charge en fonction de la résistance de charge. Les deux grandeurs sont exprimées de façon relative. La puissance par rapport à la puissance maximale et la résistance de charge par rapport à la résistance de la source.
Le maximum n'est pas très critique. Quand les résistances sont désadaptées d'un facteur 2, la puissance transférée est encore à 89 % du maximum possible.
Adaptation des lignes de transmission en transmission du signal[modifier | modifier le code]
Le problème général consiste à transmettre un signal depuis une source jusqu'à une charge (ou récepteur) distante de cette source. Ceci est résolu par l'utilisation d'une ligne de transmission entre cette charge et cette source. La source et la charge présentent en général une résistance interne R (généralement R = 50 ohms pour les signaux RF, et R = 600 ohms pour les signaux audio...).
Le principe fondamental est le suivant : en connectant sur la charge de résistance R, une ligne de transmission d'impédance caractéristique R, on retrouvera à l'autre extrémité de la ligne la même résistance R. Autrement dit, la source et la charge de résistance R seront « adaptées » si la ligne qui les relie possède une impédance caractéristique de même valeur. L'adaptation sera conservée quelle que soit la longueur de la ligne.
Par contre, si la charge présente une résistance différente de l'impédance caractéristique de la ligne, on aura des phénomènes d'ondes stationnaires. On observera alors les phénomènes suivants :
- les tensions et courants ne sont plus constants le long de la ligne : on a des « ondes stationnaires », ce qui induit plus de pertes dans la ligne ;
- une partie de l'énergie n'est plus absorbée par la charge : on a une perte de la puissance transmise à la charge ;
- si la longueur de la ligne n'est pas très petite par rapport à la longueur d'onde, la source ne verra plus une résistance fixe R, mais une impédance dépendant de la fréquence et de la longueur de la ligne. La courbe de réponse en fréquence de la ligne sera alors perturbée, ce qui peut être grave en téléphonie ou en transmission de données.
On peut quantifier ces perturbations par le rapport d'ondes stationnaires (ROS, ou SWR/VSWR pour voltage standing wave ratio) :
avec l'amplitude de l'onde incidente
l'amplitude de l'onde réfléchie
On trouve aussi d'autres indicateurs : le taux d'onde stationnaire
le return loss
avec
La mesure du ROS indique la désadaptation entre charge et ligne, et la perte de puissance associée.
À titre de données pratiques : Si une ligne d'impédance caractéristique 50 ohms est chargée par 100 ohms ou par 25 ohms, le ROS sera égal à 2, et le taux d'énergie réfléchie par la charge sera de 11 %.
Si la même ligne est chargée par 150 ohms ou par 16,6 ohms, le ROS sera de 3 et le taux d'énergie réfléchie par la charge sera de 25 %.
L'abaque de Smith permet de trouver l'impédance à l'extrémité d'une ligne de longueur donnée, chargée à l'autre extrémité par une impédance quelconque donnée.
Il est toutefois à remarquer que si la ligne qui alimente la charge est pourvue d'un dispositif d'adaptation d'impédance entre la source et l'entrée de la ligne, l'énergie réfléchie par la charge désadaptée est renvoyée en phase avec l'énergie incidente et n'est donc pas perdue, aux pertes en ligne près. Il finit par s'installer un régime d'ondes stationnaires tel que la ligne transporte une énergie incidente supérieure à l'énergie débitée par la source mais compensée par l'énergie réfléchie par la charge. Au total la charge utilise bien toute l'énergie de la source mais pas plus. Ceci implique que le dispositif de couplage au début de la ligne ne modifie pas le ROS en ligne ni à la charge. En cas de pertes en ligne, en parcourant celle-ci de la charge vers la source, le ROS s'améliore et si la ligne est très longue il peut même arriver à 1:1. Dans l'abaque de Smith, le parcours se visualise par une spirale qui tend vers le centre. En absence de pertes la spirale devient un cercle centré.
Exemples pratiques particuliers[modifier | modifier le code]
Amplificateur connecté à une ligne de transmission[modifier | modifier le code]
Dans le cas d'un émetteur radio relié à une antenne par un câble, le rendement maximal doit être obtenu, et la résistance interne de l'émetteur doit être la plus faible possible. Un amplificateur de puissance RF est ainsi conçu pour fournir sa puissance nominale sur une charge résistive standard (en général 50 ohms) mais sa résistance interne peut être beaucoup plus faible (5 à 10 ohms par exemple). La charge présente par ailleurs une impédance quelconque et est reliée par une ligne de transmission d'impédance standard. Le système d'adaptation doit dans ce cas remplir deux critères :
- minimiser les ondes stationnaires dans la ligne, qui augmentent les pertes ;
- présenter l'impédance nominale à l'amplificateur.
Un quadripôle réactif placé entre ligne et antenne, appelé adaptateur d'antenne, remplit ces deux critères. Mais d'autres variantes sont possibles :
- si la ligne est courte ou à faibles pertes, le quadripôle d'adaptation peut être entre ligne et amplificateur ;
- si l'adaptation est à une seule fréquence, une ligne de longueur et d'impédance choisie peut également remplir ce rôle.
Antenne de réception très courte devant le quart d'onde[modifier | modifier le code]
Si l'antenne a une longueur très inférieure au quart d'onde, sa résistance de rayonnement est très faible. L'antenne est alors équivalente à une capacité en série avec une résistance très petite, donc à une capacité en parallèle avec une résistance très grande. Dans ce cas, l'adaptation à la ligne de transmission est simplement impossible. C'est le cas, par exemple, d'une antenne de voiture en grandes ondes et en ondes moyennes, qui présente une résistance de rayonnement de quelques milliohms. L'antenne est reliée par une ligne courte directement sur l'étage d'entrée à haute impédance du récepteur. Si ce dernier possède un circuit accordé en entrée, on inclut la capacité constituée par l'antenne et son câble, dans la capacité d'accord de ce circuit.
Antenne d'émission fluctuante[modifier | modifier le code]
C'est le cas commun des émetteurs des téléphones portables. Comme l'impédance de l'antenne change suivant la position de la tête et les mains de l'utilisateur, l'adaptation dans toutes les circonstances est impossible, l'adaptation est alors simplement une compensation moyenne, permettant un fonctionnement satisfaisant.
Adaptation par réseau LC[modifier | modifier le code]
Un réseau LC est généralement utilisé pour obtenir une courbe de réponse en fréquence donnée. Mais il est également utilisé pour adapter la charge à la source, par exemple entre deux étages d'amplification radiofréquence. Les fréquences transmises sans atténuation sont celles pour lesquelles l'adaptation entre la source et la charge est réalisée. Par contre, l'adaptation n'aura pas lieu d'être pour les fréquences que l'on ne veut pas transmettre. Les fréquences non transmises seront réfléchies par le filtre (sauf si celui-ci possède un système de dissipation des signaux hors bande).
Le problème de l'adaptation à l'aide de composants L ou C ou de lignes, peut être traité par la méthode de l'abaque de Smith, pour les coefficients de surtension faibles ou moyens.
À la fréquence de résonance , pour les coefficients de surtension élevés (filtres sélectifs) on peut faire appel aux formules de transformations d'impédances. Ces formules sont très commodes, et sont d'autant plus précises que le Q du circuit est élevé. Les trois réseaux les plus utilisés sont le circuit LC série/parallèle, le circuit LC en π, et le circuit LC en T.
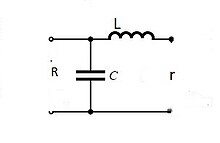
Circuit LC série/parallèle (circuit en L) : idéale pour l'adaptation d'une résistance élevée à une résistance faible. On trouve la résistance de faible valeur r en série dans le circuit LC, et la résistance de forte valeur R en parallèle sur le condensateur ou sur l'inductance .
Si Z est le module de l'impédance de l'inductance ou du condensateur (car ce sont les mêmes à la résonance), on a la condition d'adaptation : r . R = Z2.
Pour adapter r à R, il suffit donc de choisir un circuit résonant LC à la fréquence considérée, avec l'impédance Z calculée ci-dessus pour le condensateur et l'inductance.
Le Q du circuit chargé par la résistance série r est Q = Z/r, et le Q du circuit chargé par la résistance parallèle R est Q = R/Z . Comme il y a les deux résistances (source et charge), le coefficient Q est la moitié de celui calculé. On remarque que l'adaptation est réalisée quand les résistances de source et de charge amortissent identiquement le circuit LC.

Circuit LC en π : réservé pour l'adaptation de résistances élevées ou moyennes, filtrage passe-bas ou passe-haut.
Par exemple, pour un circuit passe bas en π, la résistance d'entrée R1 sera placée en parallèle sur le condensateur d'entrée C1, et la résistance de sortie R2 en parallèle sur le condensateur de sortie C2.
La condition d'adaptation sera R1/R2 = (impédance de C1/impédance de C2)2 = (C2/C1)2.
Le circuit résonant sur la fréquence considérée sera constitué par la maille C1 - L - C2, c'est-à-dire que l'inductance résonne avec C1 en série avec C2.
Le Q en charge du circuit sera d'autant plus élevé que les impédances de L, C1 et C2 seront faibles

Circuit LC en T : réservé pour l'adaptation de résistances faibles ou moyennes, filtrage passe-haut ou passe-bas.
Par exemple, pour un T passe haut (donc avec l'inductance à zéro), la résistance d'entrée R1 sera placée en série avec le condensateur d'entrée C1, et la résistance de sortie R2 en série avec le condensateur de sortie C2.
La condition d'adaptation sera R1/R2 = (impédance de C1/impédance de C2)2 = (C2/C1)2 .
Le circuit résonant sur la fréquence considérée sera constitué par l'inductance L, et par C1 en parallèle avec et C2.
Le Q en charge du circuit sera d'autant plus élevé que les impédances de L, C1 et C2 seront grandes.
Pour un circuit en T passe bas, avec condensateur central, avec l'inductance L1 côté R1 et l'inductance L2 côté R2, la condition d'adaptation sera R1/R2 = (impédance de L1/impédance de L2)2 = (L1 / L2)2
Il existe d'autres réseaux LC permettant une adaptation d'impédance : circuits LC avec pont capacitif, avec pont inductif, avec prise sur l'inductance, par « capacité en tête », etc. D'une façon générale, il faut toujours se poser la question de savoir si la résistance de charge est en parallèle (comme c'est le cas du circuit en π), configuration réservée aux résistances de charge plutôt élevées, ou si elle est en série (comme c'est le cas du circuit en T), configuration réservée aux résistances plutôt basses. On remarque que dans les deux cas, la résistance créée varie comme le carré de l'impédance qui la contrôle : si on double l'impédance, on quadruple la résistance.
Voici quatre exemples d'adaptation par circuit LC résonant.

Il faut connaître les limites de validité de ces formules :
Elles sont peu précises si Q n'est pas au moins de 3. On leur préfèrera alors l'abaque de Smith.
Le coefficient de surtension à vide Qo du circuit LC doit être nettement plus élevé que le Q en charge.
Enfin, on ne peut créer avec un circuit en π une résistance plus faible que l'impédance sur laquelle elle est placée en parallèle, et on ne peut non plus créer avec un circuit en T une résistance plus grande que l'impédance qui est en série avec cette résistance.
Distribution d'énergie électrique[modifier | modifier le code]
L'adaptation d'impédance ne concerne pas la distribution de l’énergie.
Une charge adaptée au sens de la ligne est celle qui permet le fonctionnement normal de la ligne. La charge qui correspondrait à l'adaptation conjuguée nécessiterait une tension d'entrée très supérieure à la tension de sortie de la ligne et, surtout une intensité du courant qu'il est impossible de maintenir en régime permanent[5].
Distribution de signaux vidéo[modifier | modifier le code]
Dans le cas de distribution de signaux amplifiés, le critère principal est la distorsion minimale, en particulier due aux échos de désadaptation. L'adaptation des lignes aux deux extrémités est primordiale, plus que le transfert d'énergie, le principe est alors d'utiliser des sources et des récepteurs d'impédance précisément égale à celle des lignes.
Dans le cas, par exemple, de distribution de vidéo (en studios et régies), la source est d'impédance 75 ohms, ainsi que le coaxial, et chaque utilisateur branché sur la ligne (moniteur, scope, modulateur…) est en haute impédance, et une résistance de 75 ohms ferme la ligne principale. La source « voit » donc toujours 75 ohms.
Distribution de signaux TV collectifs[modifier | modifier le code]
Pour ces fréquences VHF et UHF, on dispose de « répartiteurs » ou « coupleurs » qui présentent une résistance constante à la source des signaux, quel que soit le nombre de récepteurs connectés en sortie. Les distributeurs actifs réalisent cette condition grâce à une amplification du signal. Les distributeurs passifs réalisent grossièrement cette condition par l'utilisation de résistances, et au prix d'une atténuation du signal.
Couplage de plusieurs antennes UHF ou VHF[modifier | modifier le code]
Le problème consiste ici à mettre en parallèle deux antennes de résistance 50 ohms, et de retrouver une résistance de 50 ohms après couplage. Pour cela, on alimente tout d'abord chaque antenne par une longueur identique de câble 50 ohms. Si on mettait ensuite simplement en parallèle les deux câbles, on obtiendrait une résistance de 25 ohms, ce qui poserait un problème. Pour le résoudre, on utilise un coupleur en « té », qui joue le rôle de transformateur d'impédance. Des fabricants proposent de tels T, qui sont définis par leur bande passante et par les puissances admissibles.
Notes[modifier | modifier le code]
- (en) Conjugate matching versus reflectionless matching [PDF]
- (en) Calvert, J. B., Jacobi's Theorem Also known as the Maximum Power Transfer Theorem, misunderstanding of it retarded development of dynamos, March 30, 2001
- (en) Histoire du téléphone par James Calvert
- (en) Système Bell-Berliner - archives du Library of Congress
- Traité d'électricité, d'électronique et d'électrotechnique, volume XII, Énergie électrique, Chapitre 3 Modèles des lignes, 3.3.22 Définition : adaptation











































