Identification de système
L'identification de système ou identification paramétrique est une technique de l'automatique consistant à obtenir un modèle mathématique d'un système à partir de mesures.
Principes et objectifs[modifier | modifier le code]
L'identification consiste à appliquer ou observer des signaux de perturbation à l'entrée d'un système (par exemple, pour un système électronique, ceux-ci peuvent être de type binaire aléatoire ou pseudo-aléatoire, galois, sinus à fréquences multiples…) et en analyser la sortie dans le but d'obtenir un modèle purement mathématique. Les différents paramètres du modèle ne correspondent à aucune réalité physique dans ce cas. L'identification peut se faire soit dans le temps (espace temporel), soit en fréquence (espace de Laplace).
Éviter les modèles purement théoriques à partir des équations physiques (en général des équations différentielles), qui sont longs à obtenir et souvent trop complexes pour le temps de développement donné, est donc possible avec cette technique.
Les différents types de modèles[modifier | modifier le code]
Le principe d'une identification paramétrique est d'extraire un modèle mathématique à partir d'observations. Le modèle doit permettre de calculer la sortie du procédé y à n'importe quel instant t si les conditions initiales du système sont connues. Pour cela, on peut se servir des valeurs des entrées aux instants présent et précédents (u(t), u(t-1), ...) et des valeurs précédentes de la sortie (y(t-1), y(t-2), …) dans le cas d'un modèle régressif.
Il est tout de même important d'avoir des connaissances basiques du système pour choisir un type de modèle adapté
- Modèle possédant une entrée/une sortie (SISO) ou plusieurs entrées et plusieurs sorties (MIMO)
- Modèle linéaire ou non linéaire (dans ce cas, qu'est-ce qui est non linéaire en fonction de quoi ?)
- Modèle continu ou discret
- Modèle régressif ou indépendant : pour un modèle régressif, la sortie à un instant t, y(t), dépend des instants précédents (y(t-i)).
- Modèle stochastique ou déterministe
En général, le modèle est représenté sous forme de fonction de transfert utilisant la Transformée en Z. L'identification nécessite une structure de modèle connu a priori pour venir identifier dans cette structure différents paramètres. Voici les 3 structures de modèle les plus utilisés :
Le modèle ARX[modifier | modifier le code]
Le modèle ARX (Auto Regressive model with eXternal inputs) est un modèle auto régressif qui inclut des entrées u(t) et un bruit blanc de moyenne nulle. De plus, le modèle inclut un retard pur de k coups d'horloge. Si le système est échantillonné à une période d'échantillonnage T, alors le retard sera de k*T.
Sous forme temporelle :
Dans un espace discret utilisant la Transformée en Z :
Le modèle ARMAX[modifier | modifier le code]
Le modèle ARMAX (Auto Regressive Moving Average with eXternal inputs) reprend les attributs du modèle ARX mais inclut une fonction de transfert avec une moyenne ajustable sur le bruit blanc. En général, le bruit blanc permet de modéliser des perturbations non mesurables dans le modèle. Or, ces perturbations non mesurables (fluctuations thermiques, vibrations du sol…) sont rarement de moyenne nulle et peuvent aussi répondre à un modèle.
Le modèle ARIMAX (ou CARIMA)[modifier | modifier le code]
Dans le modèle ARIMAX (Auto Regressive Integrated Moving Average with eXternal inputs), le modèle du bruit est directement intégré :
Procédure d'identification[modifier | modifier le code]
Pour obtenir un modèle consistant, il est important d'exciter le processus avec toutes les fréquences de sa plage de fonctionnement. Le signal d'entrée appliqué doit donc être riche en fréquences (posséder un large spectre). En général, on applique un signal périodique pseudo-aléatoire (PRBS).
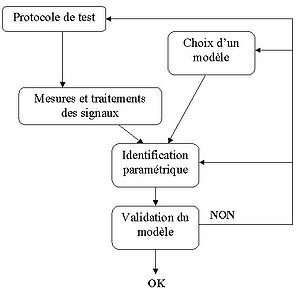
Lorsque le système possède plusieurs entrées/plusieurs sorties, il est important d'appliquer des signaux décorrélés pour ne pas introduire de biais d'identification. Une idée commune consistant à exciter l'une après l'autre les entrées est une mauvaise méthode car elle introduit un biais d'identification et ne rend pas compte du fonctionnement normal du système. Il est important de respecter une procédure rigoureuse pour identifier un procédé :
- Détermination d'un protocole de test : propriétés statistiques des signaux d'entrée pour balayer toutes les fréquences intéressantes, le ratio signal/bruit doit être suffisamment important et le nombre de points de mesures doit être significatif pour le test (>1000)
- Détermination de la structure du modèle : type de modèle, ordre et retard
- Identification : choix d'un algorithme pour trouver le modèle en minimisant les erreurs entre les mesures et le modèle, en général algorithme basé sur la méthode des moindres carrés (LS, RLS, RELS).
- Validation du modèle : Réalisation de plusieurs tests de vérification. Il est nécessaire pour cette étape d'utiliser des mesures différentes de celles utilisées lors de l'identification.
D'autres approches sont également possibles, notamment en regardant les matrices de sous-espace d'un système (mais moins efficace que ci-dessus pour les systèmes non linéaires).
Ceci peut ainsi facilement donner un modèle moins « théorique » et aider à l'amélioration du rendement, du contrôle ou de la prédiction (pour des valeurs d'action dans un système économique par exemple).
Des boîtes à outils Matlab et Scilab existent pour la résolution des algorithmes (de type ARMAX par exemple). Celles pour Octave sont à créer.
Bibliographie[modifier | modifier le code]
- Ioan Doré Landau, Identification et commande des systèmes. 2e édition revue et augmentée, Hermès, 1993 (ISBN 2-86601-365-4)
- Rapports 06008 et 05603 du Laboratoire d'analyse et d'architecture des systèmes disponibles via http://www.laas.fr
- (en) Lennart Ljung, System Identification, Theory for the User (ISBN 0-13-881640-9)
- (en) Rik Pintelon et Johan Schoukens, System Identification, A Frequency Domain Approach (ISBN 0-7803-6000-1)


![{\displaystyle Y(t)=B\cdot [u(t-k),u(t-1-k),...]^{T}-A\cdot [y(t-1),y(t-2),...]^{T}+A\cdot [\zeta (t),\zeta (t-1),...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91ac39d2491cb9cd772e1203ffad447b5d3da074)


