Théorème de Cantor-Bernstein

Le théorème de Cantor-Bernstein, également appelé théorème de Cantor-Schröder-Bernstein, est le théorème de la théorie des ensembles qui affirme l’existence d'une bijection entre deux ensembles dès lors qu'il existe deux injections, l'une du second vers le premier l'autre du premier vers le second.

Il est nommé ainsi en référence aux mathématiciens Georg Cantor, Felix Bernstein et Ernst Schröder. Cantor en donna une première démonstration, mais qui utilisait implicitement l'axiome du choix^{[réf. nécessaire]}. Bernstein en donna une démonstration qui ne dépendait pas de cet axiome. Cependant, toutes les démonstrations données utilisent le principe du tiers exclu et de ce fait ne sont pas acceptées par les intuitionnistes.

Historique

Énoncé original de Cantor (1887).

Georg Cantor énonce ce théorème sans démonstration en 1887. Le théorème se déduit par l'axiome du choix d'un résultat analogue pour les ensembles bien ordonnés démontré dans son livre Sur les fondements de la théorie des ensembles transfinis (1895-1897). Felix Bernstein, élève de celui-ci, produit une démonstration qui n'utilise pas les bons ordres (et ne nécessite pas l'axiome du choix) dès 1896 à l'âge de 18 ans. Elle est publiée en 1898 sur proposition de Cantor dans Leçons sur la théorie des fonctions sous la plume d'Émile Borel. Ernst Schröder publie lui aussi une démonstration en 1898, mais celle-ci s'avère erronée. L'erreur est repérée en 1902 par Alwin Korselt qui en fait part à Schröder début mai 1902. Celui-ci reconnaît que la paternité de la démonstration du théorème revient entièrement à Bernstein, dans une réponse envoyée quinze jours plus tard (un mois avant sa mort). Il ajoute s'être lui-même rendu compte du problème en 1901 et en avoir fait part alors à son ami Max Dehn.

Korselt soumet fin mai 1902 un article aux Mathematische Annalen, où il expose l'erreur de Schröder et propose une autre démonstration, mais celui-ci n'est publié qu'en 1911. Pendant tout ce temps la preuve de Schröder est considérée comme correcte, en particulier par Cantor, Peano et Schönflies.

Richard Dedekind en fit lui-même une démonstration en 1897 mais qui ne fut publiée qu'en 1930. Ernst Zermelo en fait une autre en 1906 qui reprend en fait les idées de Dedekind.

Énoncé

S'il existe une injection d'un ensemble $E$ vers un ensemble $F$ et une injection de $F$ vers $E$, alors il existe une bijection de $E$ sur $F$.

Explication intuitive

Si l'on considère la technique naïve qu'a un enfant pour compter le nombre d'éléments d'un ensemble, cela revient quasiment toujours à associer chacun des éléments à un autre d'un ensemble connu dont le nombre d'éléments est connu. Il peut s'agir soit d'associer chacun des éléments à compter avec l'un des doigts, soit d'associer chacun des éléments avec un nombre que l'on réciterait à haute voix (un, deux, trois, etc.), par exemple. En clair, compter se fait naïvement en effectuant une bijection d'un ensemble dont la « dimension » est connue vers un autre dont la dimension est inconnue.

Ce théorème s'interprète alors comme disant : « Si je peux compter une partie d'un ensemble avec la totalité des éléments d'un autre ensemble, et réciproquement, alors ils ont le même nombre d'éléments ». Ce qui est évident pour des ensembles finis. Ce théorème généralise alors cette notion pour des ensembles infinis.

« Si je peux compter un certain nombre de billes de mon sac de billes avec mes dix doigts, et qu'avec la totalité de mes billes, je peux les associer avec certains de mes doigts, alors j'ai exactement dix billes. »

À partir de là, ce théorème représente l'une des briques de base pour généraliser la notion de tailles d'ensembles à des ensembles infinis.

Trois démonstrations

Première démonstration

Lemme préliminaire

Commençons par montrer que si $u$ est une application injective d'un ensemble $A$ vers une de ses parties, $B$, alors il existe une bijection $v$ de $A$ sur $B$.

Théorème de Cantor-Bernstein.

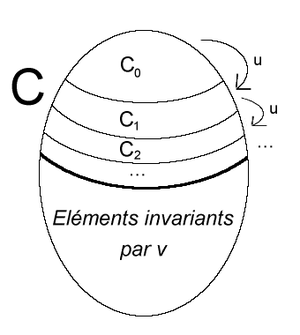
Soit $(C_{n})_{n\in \mathbb {N} }$ la suite définie par :

$\left\{{\begin{matrix}C_{0}=A\setminus B\\\forall n\in \mathbb {N} ^{*},C_{n}=u(C_{n-1})\end{matrix}}\right.$

Soit $C$ la réunion de tous les ensembles $(C_{n})_{n\in \mathbb {N} }$ : $C=\bigcup _{n\in \mathbb {N} }C_{n}$.

Soit alors $v$ l'application de $A$ dans $B$ définie par :

${\begin{matrix}v:&x\in C&\mapsto &u(x)\\&x\notin C&\mapsto &x\end{matrix}}$

$v$ est bien définie à valeurs dans $B$, car $u$ est à valeurs dans $B$, et si $x\notin C$ alors $x\notin C_{0}$ et donc $x\in B$.

$v$ envoie injectivement $C$ dans $u(C)=\cup _{n\in \mathbb {N} }u(C_{n})=\cup _{m\in \mathbb {N} ^{*}}C_{m}\subset C$ ; et le complémentaire de $C$ identiquement dans lui-même. C'est donc une injection.

Montrons que $v$ est surjective. Soit $y\in B$. Montrons qu'il existe un $x\in A$ tel que $v(x)=y$.

• Si $y\in C$ : alors il existe $i\in \mathbb {N} ^{*}$ tel que $y\in C_{i}$ ($i$ est strictement positif car $y\in B$, donc $y\notin C_{0}$). Il existe donc $x\in C_{i-1}\subset C$ tel que $v(x)=u(x)=y$.
• Si $y\notin C$ : alors $v(y)=y$

Ainsi, $v$ est bijective, ce qui démontre la première proposition.

Interprétation

On peut donner une interprétation du résultat montré ci-dessus. A est l'ensemble (infini) des spectateurs d'un théâtre (infini). Chaque spectateur a réservé une place, et initialement, on suppose que chaque place est occupée par un spectateur, mais pas forcément par le spectateur qui a réservé cette place. B est alors l'ensemble des spectateurs assis. Par ailleurs, les ensembles étant infinis, il peut rester des spectateurs debout. L'application u est l'application qui associe, à un spectateur x, le spectateur y = u(x) assis à la place de x.

$C_{0}$ est l'ensemble des spectateurs initialement debout. Ces spectateurs se rendent à leur place et en délogent les occupants. Ceux-ci forment alors l'ensemble $C_{1}$. Ces derniers procèdent de même. $C_{n}$ désigne les spectateurs debout à la n-ème étape. Ils vont aux places qu'ils ont réservées et en chassent leurs occupants. On itère une infinité de fois. C désigne l'ensemble des spectateurs qui se sont levés au moins une fois (y compris ceux qui étaient debout initialement).

L'application v désigne l'application qui associe, à un spectateur x qui doit se lever, le spectateur y qu'il va déloger, ou bien qui, à un spectateur x qui reste toujours assis, associe x lui-même. L'application réciproque de v est l'application qui, à un spectateur y qui est dérangé, associe le spectateur x qui vient prendre sa place, ou bien qui associe, à un spectateur y jamais dérangé, y lui-même.

Démonstration finale du théorème

Montrons alors le théorème initial.

Soit B = g(F) l'image de F par l'injection g. L'application u = g o f est une injection de E dans B, avec $B\subset E$. Donc il existe une bijection v de E sur B. Comme g est une injection et g(F) = B, elle définit par restriction une bijection h de F sur B. La composée h^-1∘v est une bijection de E sur F, ce qui démontre le théorème de Cantor-Bernstein.

Deuxième démonstration

Un lemme préliminaire

Cette démonstration repose sur le lemme suivant, cas particulier du théorème de Knaster-Tarski.

Soit $E$ un ensemble, $P(E)$ l'ensemble de ses parties et $G:P(E)\to P(E)$ une application croissante, c'est-à-dire telle que $A\subset B\Rightarrow G(A)\subset G(B)$. Alors $G$ admet un point fixe, c'est-à-dire qu'il existe une partie $M$ de $E$ telle que $G(M)=M$.

Démonstration finale

Soient maintenant $f$ injective de $E$ dans $F$ et $g$ injective de $F$ dans $E$. Pour toute partie $A$ de $E$, on pose $G(A)=E\setminus g\left[F\setminus f(A)\right]$, c'est-à-dire que $G(A)$ s'obtient en prenant l'image directe $f(A)$, puis le complémentaire dans $F$ de cette image, puis l'image directe par $g$ de ce complémentaire, et enfin le complémentaire dans $E$ de cette image. Il n'est pas difficile de vérifier que $G:P(E)\to P(E)$ est croissante.

On introduit alors la partie $M$ du lemme préliminaire. Cette partie est invariante par $G$, ce qui signifie que $g\left[F\setminus f(M)\right]$ est le complémentaire de $M$ dans $E$.

Théorème de Cantor-Bernstein.

On définit une bijection $h:E\to F$ en posant :

si $x\in M,h(x)=f(x)$ ;

si $x\notin M,h(x)=g^{-1}(x)$.

$M$ joue un rôle comparable à la partie $C$ dans la première démonstration ou à $E_{E}\cup E_{\infty }$ dans la démonstration qui suit.

Troisième démonstration

Cette démonstration est essentiellement celle publiée par Julius König en 1906, et souvent reprise depuis.

Supposons, sans perte de généralité, que $E$ et $F$ sont disjoints.

Théorème de Cantor-Bernstein (les ensembles $E_{E}$, $E_{F}$, $F_{F}$ et $F_{E}$ sont notés ici respectivement $E_{p}$, $E_{i}$, $F_{p}$ et $F_{i}$).

À élément $x$ de $E$, on associe une suite $(x_{0},x_{1},\dots )$ finie ou infinie définie par récurrence de la façon suivante. La valeur initiale est $x_{0}=x$. Supposons $x_{n}$ défini (sinon $x_{n+1}$ n'est pas défini), alors :

• si $x_{n}\in E$ possède un antécédent par g, alors $x_{n+1}$ est cet (unique) antécédent (remarque : dans ce cas n est pair) ;
• si $x_{n}$ est défini et $x_{n}\in F$ possède un antécédent par f, alors $x_{n+1}$ est cet (unique) antécédent (remarque : dans ce cas n est impair) ;
• dans les autres cas $x_{n+1}$n'est pas défini.

Trois cas sont alors possibles pour la suite $(x_{0},x_{1},\dots )$ qui permettent de partitionner $E$ en trois ensembles :

• $E_{E}$ est l'ensemble des $x\in E$ tels que la suite $(x_{0},x_{1},\dots )$ correspondante est finie et s'arrête sur un élément de $E$ (de façon équivalente, l'indice du dernier élément est pair) ;
• $E_{F}$ est l'ensemble des $x\in E$ tels que la suite $(x_{0},x_{1},\dots )$ correspondante est finie et s'arrête sur un élément de $F$ (de façon équivalente, l'indice du dernier élément est impair) ;
• $E_{\infty }$ est l'ensemble des $x\in E$ tels que la suite $(x_{0},x_{1},\dots )$ correspondante est infinie.

On partitionne $F$ de façon analogue en $F_{F}$, $F_{E}$ et $F_{\infty }$. Alors :

• $f$ est une bijection de $E_{E}$ sur $F_{E}$, ainsi que de $E_{\infty }$ sur $F_{\infty }$ ;
• $g$ est une bijection de $F_{F}$ sur $E_{F}$, et sa réciproque est donc une bijection de $E_{F}$ sur $F_{F}$.

On obtient ainsi une bijection de $E$ sur $F$.

Généralisation

Soient X un ensemble non vide et $\sim$ une relation d'équivalence sur l'ensemble des parties de X. On suppose qu'elle vérifie les deux propriétés :

• si $A\sim B$ alors il existe une bijection $f:A\to B$ telle que, pour toute partie $C$ de $A$, $f(C)\sim C$ ;
• si $A_{1}\cap A_{2}=B_{1}\cap B_{2}=\varnothing$ et $A_{1}\sim B_{1}$ et $A_{2}\sim B_{2}$ alors $A_{1}\cup A_{2}\sim B_{1}\cup B_{2}$.

Soient deux ensembles $A$ et $B$, un sous-ensemble $A_{1}$ de $A$ et un sous-ensemble $B_{1}$ de $B$. On suppose que $A\sim B_{1}$ et $B\sim A_{1}$. Alors $A\sim B$.

Cette généralisation peut, elle aussi, être démontrée sans l'axiome du choix.

Dans le cas particulier où $X=E\cup F$ et $\sim$ est la relation d'équipotence, on retrouve le résultat précédent.

Voir aussi

Article connexe

Propriété de Cantor-Bernstein (en)

Bibliographie

• (en) Marcel Crabbé, « Cantor-Bernstein’s Theorem in a Semiring », The Mathematical Intelligencer, vol. 33, n^o 3,‎ 2011, p. 80 (lire en ligne)
• (en) Arie Hinkis, Proofs of the Cantor-Bernstein theorem, a mathematical excursion, Birkhäuser, 2013 (ISBN 978-3-0348-0788-3, DOI 10.1007/978-3-0348-0224-6)