Variable statistique discrète
En statistique descriptive, une variable statistique est dite discrète lorsqu'elle prend un nombre fini raisonnable de valeurs numériques (note, nombre d’enfants, nombre de pièces…).
L'étude des variables statistiques discrète est un premier pas vers l'étude des statistiques dans le domaine des mathématiques élémentaires
Le caractère statistique étudié est alors appelé caractère discret.
Traitement des données[modifier | modifier le code]
Un enquête statistique consiste à prendre une population d'individus, ces individus peuvent des êtres humains (comme les élèves d'une classe) mais aussi des choses (comme les appartements d'une cité, ou des années écoulées)[1] et à s’intéresser à une propriété particulière de ces individus, appelée caractère statistique[2] : pour les élèves d'une classe, on peut s'intéresser à leur note, leur mention au bac, leur taille, ou leur marque de chaussure, pour les appartements, on peut s'intéresser à leur superficie, leur nombre de pièces et leur classe énergétique.
Lorsque ces propriétés sont numériques, le caractère étudié est dit quantitatif (taille, surface, note)[3] , dans le cas contraire, on le dit qualitatif (marque de chaussure, mention au bac, classe énergétique)[4]. Lorsque les valeurs numériques sont peu nombreuses (note, nombre de pièces d'un logement) on dit que le caractère est quantitatif discret[3]. L'étude des variables statistiques discrètes est l'étude des résultats d'une étude statistique portant sur un caractère quantitatif discret.
Les résultats d’une enquête se présentent en données brutes sous forme d'une liste désordonnée d’informations.
Exemple : Lors d'une épreuve écrite, on a relevé les notes obtenues par les élèves de la classe X : 10, 9, 12, 11, 10, 8, 14, 11, 9, 16, 5, 12, 10, 11, 10, 13
Tri des valeurs[modifier | modifier le code]
Il faut alors les trier, par ordre croissant.
Notes triées : 5, 8, 9, 9, 10, 10, 10, 10, 11, 11, 11, 12, 12, 13, 14, 16
Tableau des effectifs ou des fréquences[modifier | modifier le code]
Cette présentation sous forme de liste est peu exploitable, on décide alors de présenter les résultats de l’enquête sous forme d’un tableau d’effectifs. Chaque valeur différente de note est appelée une modalité[4].
L’effectif d’une valeur (ou d'une modalité) est le nombre de fois où cette valeur apparaît. On obtient alors le tableau suivant, appelé tableau d'effectifs
Exemple 1 : note des élèves
| notes | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| fréquences en % | 1 | 1 | 2 | 4 | 3 | 2 | 1 | 1 | 1 | 16 |
Lorsque la population étudiée est trop grande, ou bien lorsque l’on cherche à faire la comparaison entre deux populations de tailles différentes, on préfère se ramener à une population de 100, donc travailler en pourcentages, appelés ici fréquences.
Exemple 1 : note des élèves
| notes | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| fréquences en % | 6,25 | 6,25 | 12,50 | 25,00 | 18,75 | 12,50 | 6,25 | 6,25 | 6,25 | 100 |
Les tableaux peuvent se présenter sous forme verticale ou horizontale. Ainsi les deux tableaux précédents auraient tout aussi bien pu être représentés sous la forme suivante[5]:
| notes | effectifs | fréquences en pourcentages |
|---|---|---|
| 5 | 1 | 6,25 |
| 8 | 1 | 6,25 |
| 9 | 2 | 12,50 |
| 10 | 4 | 25 |
| 11 | 3 | 18,75 |
| 12 | 2 | 12,5 |
| 13 | 1 | 6,25 |
| 14 | 1 | 6,25 |
| 16 | 1 | 6,25 |
| Total | 16 | 100 |
Tableau des effectifs ou fréquences cumulés[modifier | modifier le code]
Dans l'exemple ci-dessus, il peut être intéressant de connaitre le nombre d'élèves dont la note est inférieure ou égale à 10 ou dont la note est inférieure ou égale à 8. C'est ce qu'on appelle les effectifs cumulés.
L'effectif cumulé associé à la valeur est le nombre d'individus dont le valeur du caractère statistique (ici la note) est inférieure ou égale à [6]. Il s'obtient en additionnant tous les effectifs des modalités inférieures à
Le tableau des effectifs et fréquences cumulés pour l'exemple précédent est :
| notes | effectifs cumulés | fréquences cumulées en pourcentages |
|---|---|---|
| 5 | 1 | 6,25 |
| 8 | 2 | 12,5 |
| 9 | 4 | 25 |
| 10 | 8 | 50 |
| 11 | 11 | 68,75 |
| 12 | 13 | 81,25 |
| 13 | 14 | 87,50 |
| 14 | 15 | 93,75 |
| 16 | 16 | 100 |
Le tableau se lit de la manière suivante : « 8 élèves,soit 50% de la classe, ont obtenu une note inférieure ou égale à 10 », « seuls deux élèves ont une note inférieure ou égale à 8 ».
Notion de moyenne[modifier | modifier le code]
Imaginons que nous ayons une classe d'élèves de différentes tailles et que nous désirions faire représenter la classe par un élève idéal ni trop grand ni trop petit.Y a-t-il un élève qui ait la taille « représentative » de la classe et quelle est cette taille ?
Exemple de classe (1) avec les mesures observées
| Tailles en cm | 178 | 180 | 182 | 181 | 179 |
En additionnant tous les résultats et en divisant par le nombre d'individus dans la classe, nous obtiendrons ce que l'on appelle la moyenne.
178+180+182+181+179=900
900/5 = 180
La moyenne est donc 180 cm.
Autre exemple de classe
Classe (2) plus importante avec différents élèves ayant la même taille. Nous allons compter le nombre d'élèves ayant une taille donnée et placer les résultats dans un tableau.
| 178 | 179 | 180 | 181 | 182 | Nombre d'élèves | |
| 5 | 2 | 3 | 1 | 4 | =5+2+3+1+4=15= | |
| 1785 | 1792 | 1803 | 1811 | 1824 | Somme des tailles | |
| 890 | 358 | 540 | 181 | 728 | =890+358+540+181+728=2697= |
La moyenne est ici le total des tailles à diviser par le nombre d'élèves : soit 2697/15 = 179,8 cm.
On calcule d'abord la somme des produits des mesures par le nombre de fois où l'on a observé ces mesures.
Ensuite on divise par le nombre total de mesures :
La formule générale est donc :
La moyenne est un des critères de position.
Présentation des résultats[modifier | modifier le code]
Les résultats obtenus se présentent, outre le tableau de mesures ci-dessus, par un diagramme en bâtons ou encore par un diagramme en camembert, mais cette dernière représentation représente une perte d'information et empêche de comparer le résultat statistique avec le comportement d'une variable aléatoire discrète[7].
Diagramme en bâtons[modifier | modifier le code]
Le diagramme en bâtons permet de visualiser les effectifs (ou les fréquences) associés à chaque valeur (ou modalité) de la variable.
Pour chaque valeur de la variable, on trace, au point d'abscisse un bâton vertical dont la hauteur est proportionnelle à l'effectif ou la fréquence ou la fréquence[8].
En reprenant l'étude des tailles des élèves de la classe (2), il s'agit d'élever pour chaque taille repérée un trait vertical proportionnel au nombre d'élèves. On obtient ainsi le diagramme en bâtons suivant :
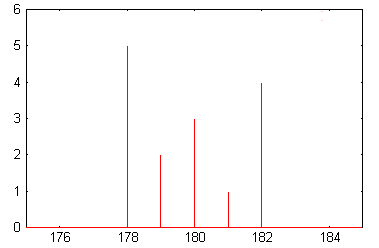
Répartition des 15 élèves selon leur taille en cm.
Il arrive que l'on donne une épaisseur (constante) à chaque bâton, ce qui donne au diagramme un aspect proche du diagramme en barres des variables non numériques (appelés variables qualitatives ou catégorielles) avec toutefois une différence importante: pour une variable qualitative, l'ordre des barres est arbitraire alors qu'il est imposé et signifiant dans le cas de la variable discrète[8].
Si on cherche à regrouper toutes les personnes ayant une taille comprise entre 179 et 180 cm dans une même classe: la classe des 179 cm - 180 cm , on est amené à traiter la variable comme continue ce qui conduit à tracer un traiter le caractère comme continu et de tracer un histogramme.
Variance et écart-type[modifier | modifier le code]
Pour voir si les résultats s’agglomèrent autour de la moyenne (courbe en forme de pic) ou au contraire s'étalent en prenant de nombreuses valeurs distinctes (courbe aplatie), on peut utiliser ce qu'on appelle un indice de dispersion. Le plus connu a pour nom variance et est défini comme suit :
où les sont les valeurs du caractère statistique, les leurs fréquences d'apparition et la moyenne.
On définit aussi l'écart-type comme étant la racine carrée de la variance
écart-type =
Exemple : Si la série comporte 3 mesures et que les nombres 3, 4 et 2 apparaissent une seule fois, la moyenne est 3 et la variance 0,667.
- Comme le calcul de la variance se fait à partir des carrés des écarts, les unités de mesure ne sont pas les mêmes que celles des observations originales. Par exemple, les longueurs mesurées en mètres (m) auront une variance mesurée en mètres carrés (m²).
- L'écart-type, correspondant à la racine carrée de la variance nous donnera par contre l'unité utilisée dans l'échelle originale.
Références[modifier | modifier le code]
- Ambrosini 2011, p. 5.
- Ambrosini 2011, p. 6.
- Ambrosini 2011, p. 10.
- Ambrosini 2011, p. 7.
- Ambrosini 2011, p. 15.
- Ambrosini 2011, p. 30.
- Ambrosini 2011, p. 25.
- Ambrosini 2011, p. 26.
Bibliographie[modifier | modifier le code]
- Christian Ambrosini, « Éléments de statistique descriptive »,















