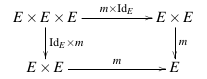Associativité
En mathématiques, et plus précisément en algèbre générale, une loi de composition interne ou loi interne sur un ensemble E est dite associative si pour tous x, y et z dans E :
- .
En notant , l'associativité se traduit par le diagramme commutatif suivant :
Parmi les lois associatives, on peut citer les lois d'addition et de multiplication des nombres réels, des nombres complexes et des matrices carrées, l'addition des vecteurs, et l'intersection, la réunion d'ensembles. Aussi, si M est un ensemble quelconque et S désigne l'ensemble de toutes les fonctions de M vers M, alors l'opération de composition des fonctions sur S est associative.
Parmi les lois non associatives, on peut citer par exemple le produit vectoriel sur un espace euclidien orienté de dimension 3.
Un autre exemple est la soustraction des nombres réels. En effet :
- et
donc
- .
Un ensemble muni d'une loi interne associative et unifère est appelé un monoïde.
On peut écrire un algorithme qui, pour un magma fini d'ordre de table de Cayley donnée, détermine s'il est un groupe ou non en opérations élémentaires[1], la difficulté majeure étant de décider de l'associativité de la loi.
Référence[modifier | modifier le code]
- Jean Vuillemin (en), « Comment verifier l'associativite d'une table de groupe », Theoretical Computer Science, vol. 4, no 1, , p. 77-82 (lire en ligne).