Vent thermique

b) augmente avec Z dans une atmosphère barocline ()
Le vent thermique est un concept pratique en météorologie pour calculer la variation du vent entre deux altitudes quand on connaît la structure thermique de la masse d'air[1].
Définition[modifier | modifier le code]
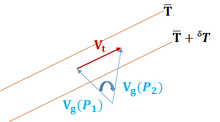
Dans une couche de l'atmosphère terrestre, limitée par des surfaces isobares inférieures (p0) et supérieure (p1), le vent V soufflant en un point n'est généralement pas le même, ni par sa direction ou vitesse, au sommet et à la base de la couche. La différence vectorielle représente ce cisaillement vertical subi par le vent entre le bas et le haut de la couche et il définit le « Vent thermique » (VT)[2] :
Le vent étant dû à un équilibre entre différentes forces que sont le gradient de pression, la force de Coriolis, la gravité, la force centrifuge et la friction. À grande échelle, dite échelle synoptique, et suffisamment haut pour que la friction du terrain soit négligeable, la pression et Coriolis demeurent les seules forces dans l'équation. Il s'agit de l'équilibre géostrophique qui donne le vent géostrophique. Le vent géostrophique selon les axes x et y à une altitude de (Z) de pression constante est défini dans l'atmosphère libre comme[3] :
Le vent thermique devient donc :
Selon cet équilibre, on utilise l'hypothèse hydrostatique et la loi des gaz parfaits pour calculer la relation entre la pression (p) et la température (T):
En combinant ces équations, on obtient la relation qui donne le vent thermique ():
- Où:
- = facteur (ou paramètre) de Coriolis = ;
- vg et ug sont les composantes selon x et y du vent géostrophique ;
- est le géopotentiel ;
- = Vitesse angulaire de rotation de la Terre ;
- = latitude ;
- R = constante des gaz parfaits ;
- g = accélération gravitationnelle = 9,81 m/s2 ;
- selon l'axe z.
- Où:
Formulation avec les températures[modifier | modifier le code]

Si on prend une température moyenne dans la couche entre et comme , l'équation pour le vent thermique devient[2] :
ou sous forme différentielle
Remarque:les différentiations étant à pression constante, on peut aussi écrire la formule en fonction de la température potentielle.
Le vent thermique est donc perpendiculaire au gradient de T, avec les températures les plus basses à gauche dans l'hémisphère nord (à droite dans celle du sud).
Formulation avec le géopotentiel[modifier | modifier le code]
Ou si on transforme cette équation en utilisant le géopotentiel[3],[4] :
Ce qui donne :
Le vent thermique est donc perpendiculaire au gradient , avec le géopotentiel le plus bas à gauche dans l'hémisphère nord (à droite dans celle du sud).
Nota : Le vent thermique est indéterminé près de l'équateur puisque y est nul et que devient infini.
Propriétés[modifier | modifier le code]
À partir de la formulation du vent thermique, il est possible d'en déduire trois propriétés[2] :
- Il est tangent aux lignes d'égale valeur de la température moyenne — ou de l'épaisseur géopotentielle — dans la couche ;
- De part et d'autre de ces isolignes, il laisse les températures moyennes plus basses sur sa gauche dans l'hémisphère Nord, sur sa droite dans l'hémisphère Sud ;
- Son intensité est proportionnelle au gradient isobare de la température moyenne dans la couche.
Usage[modifier | modifier le code]
Fronts et courant-jet[modifier | modifier le code]

Selon la définition ci-dessus, une masse d'air où la variation de température avec l'altitude est la même partout n'aura aucun vent thermique. Le vent sera le même à toutes les altitudes, c'est ce qu'on appelle une masse d'air barotrope. Par contre, lorsqu'il y a une variation de la température moyenne quand on se déplace selon x ou y, cela implique que le vent variera avec l'altitude et c'est alors une atmosphère barocline[5].
Dans la réalité, il y a généralement des contrastes thermiques dans l'atmosphère. En effet, les pôles et l'équateur ne sont pas réchauffés de la même façon par le Soleil à cause de l'angle d'incidence des rayons solaires. Comme les températures les plus froides sont aux pôles et les plus chaudes à l'équateur, le gradient de températures est dirigé vers l'équateur. Par la définition du vent thermique, il va suivre la perpendiculaire à ce gradient (les isothermes) et être de direction générale d'ouest vers est[5]. Cependant, la distribution de température n'est pas uniforme à cause des mouvements de l'air et le vent thermique se repère donc facilement sur une carte météorologique par les zones où la températures change rapidement : les zones frontales. La frontogénèse est le processus de formation ou d'intensification de ces fronts, associé au vent thermique[6].
Dans ces zones, le vent change rapidement avec l'altitude et donne naissance au courant-jet[5]. Cependant, à la tropopause, la température devient stable avant de réchauffer dans la stratosphère. Comme la tropopause est plus basse aux pôles qu'à l'équateur, le vent thermique change donc de direction à ce niveau car la température se réchauffe plus rapidement au nord ce qui inverse le gradient de température et donc le vent thermique. C'est ce qui forme le sommet du courant-jet.
Advection de température[modifier | modifier le code]

Si le vent géostrophique tourne avec l'altitude, il transporte de l'air d'une certaine température depuis une zone vers une autre qui a une température différente. Il s'agit d'advection chaude ou froide selon le cas. Ceci change la distribution thermique et naturellement crée un vent thermique.
Une advection d'air chaud par le vent géostrophique va donc créer un gradient thermique perpendiculaire au vent et donc un vent thermique vers l'est ce qui cause une rotation dextrogyre des vents en altitude. L'inverse se produit pour une advection froide.
Notes et références[modifier | modifier le code]
- Organisation météorologique mondiale, « Vent thermique », sur Eumetcal (version du sur Internet Archive).
- « Le vent thermique », Glossaire météorologique, sur Météo-France (version du sur Internet Archive).
- Holton 2004, p. 68-71 où le géopotentiel est transformé en Z
- Écoulement en équilibre, Département de sciences de la Terre et de l'atmosphère de l'UQAM (lire en ligne [PDF]).
- E. Monteiro, « Cours 8 : Structure verticale du vent géostrophique, le vent thermique » [PDF], Météorologie dynamique, UQÀM, (consulté le ).
- Organisation météorologique mondiale, « Frontogénèse », sur Eumetcal (version du sur Internet Archive).
Bibliographie[modifier | modifier le code]
- (en) James R. Holton, An Introduction to Dynamic Meteorology, Amsterdam, Elsevier academic press, , 535 p. (ISBN 0-12-354015-1, lire en ligne)
- Sylvie Malardel, Fondamentaux de Météorologie : à l'école du temps, Toulouse, Cépaduès-éd., , 314 p. (ISBN 2-85428-631-6)
- (en) Tim Vasquez, Weather Forecasting Handbook, , 198 p. (ISBN 0-9706840-2-9)

























