Snark (graphe)


En théorie des graphes, une branche des mathématiques, un snark est un graphe cubique connexe, sans isthme et d'indice chromatique égal à 4. En d'autres termes, c'est un graphe dans lequel chaque sommet a trois voisins, et dont les arêtes ne peuvent pas être colorées avec seulement 3 couleurs sans que deux arêtes de même couleur ne se rencontrent en un même sommet (d'après le théorème de Vizing, l'indice chromatique d'un graphe cubique est 3 ou 4).
Pour éviter les cas triviaux, on exige souvent de plus que les snarks aient une maille d'au moins 5.
Les snarks ont été nommés ainsi par le mathématicien américain Martin Gardner en 1976, d'après l'objet mystérieux et insaisissable du poème La Chasse au Snark de Lewis Carroll[1].
Historique[modifier | modifier le code]
Peter Guthrie Tait a initié l'étude des snarks en 1880, quand il a prouvé que démontrer le théorème des quatre couleurs revenait à démontrer que tout graphe cubique planaire pouvait avoir ses arêtes colorées avec trois couleurs. Ou dit autrement, qu'aucun snark n'est planaire[2].
Le premier snark connu était le graphe de Petersen, découvert en 1898. En 1946, le mathématicien croate Danilo Blanuša découvrit deux autres snarks, tous deux à 18 sommets, à présent appelés les snarks de Blanuša[3]. Le quatrième snark connu a été découvert deux ans plus tard par Bill Tutte, sous le pseudonyme de Blanche Descartes, et comportait 210 sommets[4],[5]. En 1973, George Szekeres a découvert le cinquième snark connu, le snark de Szekeres[6]. En 1975, Rufus Isaacs a généralisé la méthode de Blanuša afin de construire deux familles infinies de snarks : les snarks fleurs et les BDS ou snarks de Blanuša-Descartes-Szekeres, une famille qui comprend les deux snarks de Blanuša, le snark de Descartes et le snark de Szekeres[7]. Isaacs découvrit aussi un snark à 30 sommets qui n'appartient pas à la famille BDS et qui n'est pas un snark fleur : le snark double étoile.
Écrivant dans The Electronic Journal of Combinatorics, Miroslav Chladný affirme que « En étudiant les nombreux problèmes importants et difficiles de la théorie des graphes (comme la conjecture du double recouvrement et la conjecture du 5-flux, on tombe sur une sorte intéressante de graphes quelque peu mystérieuse appelés snarks. En dépit de leur simple définition … et après plus d'un siècle d'investigations, leurs propriétés et leur structure restent largement inconnues[8]. »
Propriétés[modifier | modifier le code]
Tous les snarks sont non-hamiltoniens, et plusieurs snarks connus sont hypohamiltoniens : en supprimant n'importe quel sommet, le graphe devient hamiltonien. Un snark hypohamiltonien est forcément bicritique : en supprimant n'importe quelle paire de sommets, les arêtes du graphes peuvent être colorées avec 3 couleurs[9],[10].
On a pu démontrer que le nombre de snarks ayant un nombre pair donné de sommets est minoré par une fonction exponentielle de ce nombre de sommets[11] (comme les snarks sont des graphes cubiques, ils ont forcément un nombre de sommets pair). La suite A130315 de l'OEIS donne le nombre de snarks non triviaux à sommets pour les petites valeurs de : 0, 0, 0, 0, 1, 0, 0, 0, 2, 6, 20, 38, 280, 2900, 28399, 293059, 3833587, 60167732.
Conjecture du double revêtement[modifier | modifier le code]
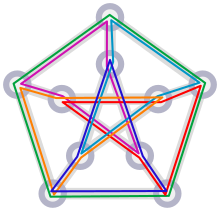
La conjecture du double revêtement (en) affirme que dans tout graphe sans isthme, on peut trouver un ensemble de cycles passant deux fois par chaque arête. Une formulation équivalente est que le graphe peut être plongé (en) dans une surface de telle sorte que toutes les faces du plongement soient des cycles simples.
Les snarks forment le cas difficile dans cette conjecture : si elle est vraie pour les snarks, elle le sera pour tous les graphes[12].
En rapport avec ce problème, Branko Grünbaum a émis la conjecture qu'il était impossible de plonger un graphe sur une surface de sorte que toutes les faces soient des cycles simples et que deux faces quelconques soit soient disjointes soit partagent une seule arête commune. Cette conjecture s'est révélée fausse, Martin Kochol ayant trouvé un contre-exemple[13],[14],[15].
Théorème du snark[modifier | modifier le code]
W. T. Tutte a émis la conjecture que tout snark a le graphe de Petersen comme mineur. En d'autres termes, il a émis l'hypothèse que l'on pouvait obtenir le plus petit snark, le graphe de Petersen, à partir de n'importe quel autre snark en contractant certaines arêtes et en supprimant des sommets isolés ou des arêtes.
Une hypothèse équivalente est que tout snark peut être formé à partir du graphe de Petersen en subdivisant certaines de ses arêtes par homéomorphisme.
En 1999, Neil Robertson, Daniel Sanders, Paul Seymour et Robin Thomas ont annoncé une démonstration de la conjecture de Tutte[16]. Sarah-Marie Belcastro fait néanmoins remarquer qu'en 2012, leur démonstration reste en grande partie non publiée.
Tutte a également émis une conjecture généralisant le théorème du snark à des graphes arbitraires : tout graphe sans isthme et sans graphe de Petersen comme mineur un flux nulle part nul de type 4 (en). Cela signifie que les arêtes du graphe peuvent se voir affecter une orientation et un nombre égal à 1, 2 ou 3, de façon que la somme des nombres entrants moins la somme des nombres sortants soit divisible par 4 quel que soit le sommet. Comme Tutte l'a montré, pour les graphes cubiques une telle affectation existe si et seulement si les arêtes peuvent être colorées avec 3 couleurs, donc la conjecture découle du théorème du snark dans le cas des graphes cubiques. Néanmoins, la conjecture reste ouverte pour les autres graphes[17].
Liste de snarks[modifier | modifier le code]
- Graphe de Petersen (10 sommets, découvert en 1898)
- Graphe de Tietze (12 sommets, mais avec une maille de 3, en général pas considéré comme un snark)
- Premier snark de Blanuša et second snark de Blanuša (18 sommets ; découvert en 1946)
- Snark de Descartes (famille finie de graphes à 210 sommets ; découvert par Bill Tutte en 1948)
- Snark double étoile (30 sommets)
- Premier snark de Celmins-Swart, second snark de Celmins-Swart
- Premier snark de Loupekine, second snark de Loupekine
- Snark de Szekeres (50 sommets ; découvert en 1973)
- Snark de Watkins (50 sommets ; découvert en 1989)
- Snark fleur (famille infinie à 20, 28, 36, 44... sommets, découverte en 1975)
- Snark de Goldberg (autre famille infinie)
En 2012, Gunnar Brinkmann, Jan Goedgebeur, Jonas Hägglund et Klas Markström ont généré tous les snarks jusqu'à 36 sommets grâce à une recherche par ordinateur[18].
Notes et références[modifier | modifier le code]
- (en) Martin Gardner, « Mathematical Games », Scientific American, vol. 4, no 234, , p. 126 à 130
- (en) Peter Guthrie Tait, « Remarks on the colourings of maps », Proc. R. Soc. Edinburgh, vol. 10, , p. 729
- (hr) Danilo Blanuša, « Problem četiriju boja », Glasnik Mat. Fiz. Astr. Ser II, vol. 1, , p. 31 à 42
- (en) Blanche Descartes, « Network-colourings », The Mathematical Gazette (London), no 32, , p. 67 à 69
- (en) Martin Gardner, The Last Recreations : Hydras, Eggs, and Other Mathematical Mystifications, Springer, , 392 p. (ISBN 978-0-387-25827-0, lire en ligne).
- (en) George Szekeres, « Polyhedral decompositions of cubic graphs », Bull. Austral. Math. Soc., vol. 8, no 3, , p. 367 à 387 (DOI 10.1017/S0004972700042660)
- (en) Rufus Isaacs, « Infinite families of non-trivial trivalent graphs which are not Tait-colorable », American Mathematical Monthly, vol. 82, no 3, , p. 221 à 239 (DOI 10.2307/2319844, JSTOR 2319844)
- (en) Miroslav Chladný et Martin Škoviera, « Factorisation of snarks », The Electronic Journal of Combinatorics, vol. 17, , p. 32
- (en) E. Steffen, « Classification and characterizations of snarks », Discrete Mathematics, vol. 188, nos 1–3, , p. 183 à 203 (DOI 10.1016/S0012-365X(97)00255-0, MR 1630478)
- (en) E. Steffen, « On bicritical snarks », Math. Slovaca, vol. 51, no 2, , p. 141 à 150 (MR 1841443)
- (en) Zdzisław Skupień, « Exponentially many hypohamiltonian snarks », dans 6th Czech-Slovak International Symposium on Combinatorics, Graph Theory, Algorithms and Applications, coll. « Electronic Notes in Discrete Mathematics » (no 28), , 417 à 424 (DOI 10.1016/j.endm.2007.01.059)
- (en) F. Jaeger, « A survey of the cycle double cover conjecture », dans Annals of Discrete Mathematics 27 – Cycles in Graphs, vol. 27, , 1 à 12 (ISBN 978-0-444-87803-8, DOI 10.1016/S0304-0208(08)72993-1).
- (en) Martin Kochol, « Snarks without small cycles », Journal of Combinatorial Theory, Series B, vol. 67, , p. 34 à 47.
- (en) Martin Kochol, « 3-Regular non 3-edge-colorable graphs with polyhedral embeddings in orientable surfaces », dans Graph Drawing 2008, Editors: I.G. Tollis, M. Patrignani, vol. 5417, , 319 à 323.
- (en) Martin Kochol, « Polyhedral embeddings of snarks in orientable surfaces », dans Proceedings of the American Mathematical Society, vol. 137, , 1613 à 1619.
- (en) Robin Thomas, « Recent Excluded Minor Theorems for Graphs », dans Surveys in Combinatorics, 1999, Cambridge University Press, , 201 à 222 (lire en ligne)
- (en) 4-flow conjecture, Open Problem Garden.
- (en) Gunnar Brinkmann, Jan Goedgebeur, Jonas Hägglund et Klas Markström, « Generation and Properties of Snarks », arXiv, (lire en ligne)
Voir aussi[modifier | modifier le code]
Crédit d'auteurs[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Snark (graph theory) » (voir la liste des auteurs).
Liens externes[modifier | modifier le code]
- (en) Eric W. Weisstein, « Snark », sur MathWorld
- (en) Sarah-Marie Belcastro, « The continuing saga of snarks », The College Mathematics Journal, vol. 43, no 1, , p. 82 à 87 (DOI 10.4169/college.math.j.43.1.082, MR 2875562), une excellente vulgarisation du sujet.



