sRGB
sRGB, ou standard RGB (« Red Green Blue », en français « Rouge Vert Bleu normal »), est l'espace de couleur par défaut proposé pour les dispositifs numériques, notamment les écrans d'ordinateurs, par Hewlett-Packard et Microsoft en 1996.
La norme CIE 61966-2-1 (1999) définit l'espace de couleurs sRGB comme « un espace chromatique commun pour le stockage », de façon que les équipements d'origine et de système d'exploitation divers puissent communiquer simplement[1]. Elle se base sur le corps de normes et méthodes colorimétriques définies depuis 1931 et reprend la technologie éprouvée de la télévision que décrit la recommandation ITU-R BT.709 sur l'image vidéo[2].
Présentation[modifier | modifier le code]
Dans les dernières années du XXe siècle les ordinateurs personnels commencent à utiliser des écrans en couleurs et à communiquer entre eux par internet, tandis que l'augmentation de la puissance de calcul des circuits permet la circulation d'images photographiques. Pour faciliter ces échanges, un fabricant de matériel, Hewlett-Packard et un diffuseur de systèmes d'exploitation, Microsoft, proposent un système de description des couleurs par défaut, c'est-à-dire qui sert quand le programme n'indique aucun profil de couleur particulier. La Commission internationale de l'éclairage publie la norme en 1999[3].
À cette époque, plusieurs espaces de couleur rouge-vert-bleu coexistent, la plupart dépendant d'un industriel ou adaptés à un emploi particulier : ISO RGB[4], sRGB, Adobe RGB, Apple RGB, etc. plus les espaces video. La communication d'images aboutit quelquefois à des rendus décevants. sRGB est destiné à l'image multimedia, et tient compte du voile que cause l'éclairage ambiant sur l'écran[5].
Les écrans d'ordinateur reproduisent les couleurs par synthèse additive à partir de trois primaires. L'unité centrale envoie à l'écran, pour chaque point (pixel), trois valeurs numériques correspondant à la luminosité de chaque primaire à cet endroit.
Les premiers écrans d'ordinateurs fonctionnaient avec un tube cathodique, comme ceux de la télévision. La norme sRGB reprend, en l'adaptant à l'informatique, celle qui régit la vidéo. Le codage de la luminosité est non linéaire par rapport à la luminance, avec une correction gamma. Les écrans plats, plus récents, fonctionnent avec le même signal que leurs prédécesseurs. Le terminal reçoit les valeurs données dans l'espace sRGB. Les utilisateurs qui en ont besoin intercalent un logiciel qui les corrige à partir du profil ICC du périphérique.
L'espace de couleur sRGB est devenu le mode par défaut pour la plupart des secteurs de l'imagerie numérique, comme pour la photographie. Les fabricants proposent en outre des formats plus adaptés à leur usage, souvent propriétaires[6].
Caractéristiques principales[modifier | modifier le code]
- Gamme de couleurs
Le système permet de reproduire environ 40 % des couleurs que la vision humaine peut distinguer. Les primaires sont légèrement désaturées, ce qui leur permet d'être plus lumineuses. sRGB abandonne la région des vert-jaunes à vert-bleus, dans laquelle la discrimination des couleurs est plus faible, au profit notamment de la zone peu chromatisée, où l'on distingue le plus de nuances. Cet avantage se perd si l'on éloigne, comme dans Adobe RGB, la primaire verte, sans augmenter la profondeur de couleur au-delà de 8 bits[7].
- Valeurs
Les valeurs des composantes dans l'espace sRGB sont comprises entre 0 et 1. La norme sRGB ne fixe pas la profondeur de couleur. Lorsque ces valeurs sont codées sur un octet, comme il arrive souvent dans les applications, la valeur sRGB est exprimée en 1/255 ; par exemple le code de couleur #FF8040 se décompose en trois valeurs codées sur un octet entre 0x00 et 0xFF, correspondant, dans l'ordre à une composante rouge codée 0xFF, donnant une valeur de 255/255 = 1, et, similairement, une composante verte codée 0x80 donnant une valeur de 128/255 (≈ 0,5) et une composante bleue codée 0x40 donnant une valeur de 64/255 (≈ 0,25).
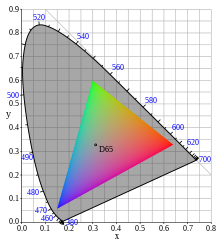
- Chromaticité
Le point blanc, obtenu avec les trois composantes égales, correspond à l'illuminant D65. Les coordonnées des couleurs primaires de l'espace de couleurs sRGB — reprises de la norme de télévision HD — dans l'espace CIE xyY sont :
| x | y | λ | pureté d'excitation | |
| Blanc (D65) | 0,3127 | 0,3290 | — | 0 |
| Rouge | 0,64 | 0,33 | 612 nm | 92 % |
| Vert | 0,30 | 0,60 | 547 nm | 74 % |
| Bleu | 0,15 | 0,06 | 464,5 nm | 93 % |
- Luminosité
Le calcul de la luminance relative d'un pixel implique de passer d'abord dans un espace de couleurs linéaire. Si C représente la valeur d'un canal r, g (vert) ou b et Clin représente la valeur linéaire utilisable pour le calcul de la luminance :
- où .
La luminance relative s'obtient ensuite à partir de ses valeurs rlin, glin, blin par la formule :
Pour obtenir une valeur de luminosité perçue, non linéaire, on peut appliquer la formule CIE ; ou, si l'on veut, appliquer la correction gamma inverse. En effet, si les trois canaux rouge, vert et bleu ont la même valeur, celle-ci est une assez bonne estimation de la luminosité, sans aucun calcul[8]. On peut donc rechercher une valeur compatible dans les autres cas.
Conversions entre CIE et sRGB[modifier | modifier le code]
Les conversions de l'espace sRGB vers les espaces colorimétriques CIE se ramènent, finalement, à un changement de coordonnées dans un espace. Il existe des matrices de conversion entre tous les espaces linéaires.
Avant d'appliquer ces matrices, il faut effectuer la transformation non-linéaire.
Transformation de CIE XYZ vers sRGB[modifier | modifier le code]
- Conversion CIE xyY en CIE XYZ
Si on part de valeurs de l'espace de couleurs CIE xyY (avec x, y les coordonnées chromatiques et Y la luminance), il faut d'abord les transformer en valeurs CIE XYZ :
- Conversion CIE XYZ vers sRGB (linéaire)
Le premier pas dans le calcul des valeurs du triplet sRGB à partir de celles du triplet CIE XYZ est une transformation linéaire, que résume une multiplication matricielle[a].
- Ces valeurs RGB linéaire ne sont pas le résultat final.
Les valeurs initiales X, Y, et Z doivent être exprimées dans la plage [0,1].
Si les paramètres intermédiaires , et sont hors de la plage [0,1], la couleur est hors du gamut sRGB et les écrans conformes ne peuvent les reproduire. Si c'est le cas, divers procédés permettent de trouver la meilleure approximation. Si les valeurs sont celles d'une image, on considère l'ensemble. S'il s'agit d'une valeur isolée, on peut rechercher la valeur qui présente un écart de couleur minimal suivant CIE LUV ; en général on se contente de tronquer à 1 les valeurs supérieures. Un triplet (1,1,1) représente un affichage blanc. Ce blanc correspond, pour les écrans conformes, à un illuminant D65, et à un triplet (X,Y,Z) = (0.9505, 1.0000, 1.0890)[b].
La formule suivante transforme les valeurs linéaires en sRGB. Si représente , , ou , et représente , ou :
- où
Ces valeurs converties sont dans la plage allant de 0 à 1. Si les valeurs dans la plage 0 à 255 sont nécessaires, par exemple pour un affichage sur un périphérique vidéo de 8 bits, on à multiplie par 255 et on tronque ou arrondit à l'entier[c].
Transformation de sRGB vers CIE XYZ[modifier | modifier le code]
Les valeurs sRGB , , se trouvent dans la plage allant de 0 à 1.
où C est R, V, ou B). suivi par une multiplication matricielle des valeurs linéaires pour obtenir XYZ:
Principes[modifier | modifier le code]
Loi de puissance[modifier | modifier le code]
Le signal des canaux rouge, vert et bleu du signal sRGB n'est pas proportionnel à la luminance. Dès 1939, les premiers concepteurs de la télévision ont remarqué que la non-linéarité des tubes cathodiques des téléviseurs vis-à-vis des grandeurs physiques était similaire à celle de la vision humaine[9]. Selon la loi de Stevens, la perception des stimulus lumineux suit une loi de puissance, de la même espèce que celle qui s'observe dans les tubes cathodiques. Sur cette échelle non-linéaire, deux luminosités à la limite du seuil de discrimination se représentent par deux niveaux espacés de la même valeur.
Cette coïncidence entre perception et réponse du tube cathodique simplifiait grandement le traitement du signal. Le traitement non-linéaire est bien plus complexe qu'un simple amplificateur électronique. Une correction de gamma restait nécessaire, parce que les tubes des caméras donnaient un signal lié à la luminance par une loi de puissance différente de ceux des téléviseurs. Il suffisait d'un élément non linéaire au départ des studios pour fournir un signal adéquat pour les milliers ou millions de téléviseurs du public.
Le bruit de fond électronique s'ajoute uniformément au signal. Si celui-ci était linéaire, il serait sensible lorsque le niveau du signal est faible, dans les parties sombres. Avec une loi de puissance, il tend à se répartir sur toute l'image, quelle que soit la luminosité.
Les écrans plats ont remplacé les tubes cathodiques, mais la perception humaine demeure, justifiant la loi de puissance pour l'encodage des couleurs dans les écrans. Elle permet d'obtenir un maximum de nuances distinctes, alors qu'une loi linéaire, avec huit bits, aboutirait à la posterisation dans les basses lumières et à des codes donnant des couleurs indiscernables dans les hautes lumières.
Rampe linéaire dans les basses lumières[modifier | modifier le code]
La lumière diffuse dans l'environnement de l'écran joue aussi un rôle. Elle éclaire la surface de l'écran, qui en rediffuse une partie vers le spectateur. Cette lumière forme un voile, sensible quand l'écran est très sombre. Le niveau le plus bas du signal ne correspond donc pas à l'obscurité (luminance zéro), mais à ce voile.
Lorsque la puissance que rayonne l'écran est proche de ce voile, la couleur est plus pâle que ce qu'elle devrait être. Pour se rapprocher la bonne couleur, on prolonge la fonction de puissance, à partir d'un point un peu au-dessus du niveau du voile calculé pour l'environnement que prévoit la norme, par un segment droit jusqu'à zéro.
Réalisation logicielle[modifier | modifier le code]
L'élévation à une puissance avec une décimale est une opération relativement coûteuse en puissance de calcul. Pour éviter de la répéter pour chaque pixel. Les ordinateurs ont souvent recours à une table de correspondance (dite LUT pour Look Up Table).
Remarques[modifier | modifier le code]
- Correction de gamma
Le système sRGB a été conçu pour refléter un moniteur typique de l'époque avec une valeur gamma de 2,2 (en vidéo analogique et une page du noir au blanc codant les composantes colorimétriques de 10 à 235 sur une échelle de 0 à 255)[d] ; avec les moniteurs sRGB numériques d'aujourd'hui, cela a été ajusté pour correspondre où la plage du noir au blanc code les composantes colorimétriques de 0 à 255 sans discontinuité avec un gamma de 2,4, mais l'ajustement du noir nécessite de corriger de façon linéaire la luminosité linéaire des composantes colorimétriques codées de 0 à 10, et d'étendre la courbe au delà des composantes codées de 235 à 255: cette extension de plage de rendu augmente la gamme colorimétrique affichable pour les graphiques et documents numériques stables, même si ces valeurs très sombres et très claires sont assez facilement saturées et ne conviennent généralement pas à la vidéo en images naturelles, où elles provoquent des artefacts visibles parfois perturbants, comme des aplats saturés sur les photos ou scènes peu animées ou des moirées instables, créant des objets fantômes en vidéo animée (par exemple pour le rendu du relief des visages dans une scène éclairée) ou la réduction de la gamme discernable de couleurs et la stabilité des ombrages.
Dans les zones peu éclairées (celles où la transformation sRGB est linéaire et n'obétit pas à la règle du gamma, ces fantômes deviennent très visibles et masquent tout le reste des détails : textures et lignes de contraste d'objets réels qui sont dès lors complètement masqués par les fantômes et moirées produits par ces textures, lesquelles sont traitées de la même façon que le "bruit" de quantification intrinsèque des images numériques, dans ces intervalles limites de basses et haute luminosité et de colorimétrie très approximative s'il n'y a pas un traitement particulier pour gommer le "bruit "systématique de quantification en le remplaçant par un bruit blanc aléatoire, comme c'était le cas en télévision analogique, même si les moirés existaient dans les zones très éclairées ou à fort contraste). Une autre solution de gommage de cet effet consiste aussi dans les codecs vidéos numériques à augmenter la fréquence des trames en prenant en compte les images interpolées intermédiaires pour lisser ces fantômes dans les trames finales, et à utiliser des quantifications moins systématiques comportant des seuils plus aléatoires spatialement (sur la surface 2D d'une trame et dans la dimension du temps entre les trames en vidéo animée), mais cela demande un traitement numérique plus complexe (et plus de mémoire pour traiter une vidéo).
Sans ce traitement complexe, l'espace sRGB ne devrait donc pas utiliser les valeurs colorimétriques très faibles et très élevées pour la photo numérique et la vidéo, mais rester dans l'espace restreint de 10 à 235 (au lieu de 0 à 255 sur l'échelle complète) pour éviter la saturation, et les effets néfastes des systèmes de quantification simples (sans post-traitement numérique avec une accélération matérielle, beaucoup de mémoire). Dans cet espace alors la valeur gamma du sRGB est stable et vaut 2,4, il n'y a pas de "vrais noir" ni de "vrais blancs", qui ne peuvent servir qu'au détourage ou au sous-titrage (avec éventuellement un contraste qui peut être accentué pour ces éléments fixes de l'image, si l'écran le permet mais pas en VGA, ni sur un écran cathodique ou les valeurs faibles sont réservées à l'extinction du balayage électronique les des retours de ligne ou changements de trame), mais au moins la colorimétrie est suffisante partout (même en passant au rendu dit HDR, qui ne fait qu'ajouter des bits de précision aux composantes colorimétriques sans changer l'étendue des valeurs ni les fonctions de transferts et d'ajustement gamma, mais permet aussi de se passer du traitement spatial de l'image pour gommer les moirés et aplats de saturation qui sont fortement atténués par cette augmentation de la précision, notamment dans les zones d'ombre si les composantes colorimétriques sont codées en virgule flottante et non plus simplement avec des entiers).
Enfin sRGB n'est qu'un modèle idéalisé pour les écrans trichromatiques (ou monochromes), il n'est pas adapté à l'impression ou aux écrans plus modernes qui peuvent utiliser plus de composantes, avec des fonctions de transfert plus complexes (et différentes valeur de gamma selon la composante, sa précision et sa résolution spatiale ou temporelle), ce modèle reste idéalisé sur les anciens écrans cathodiques, tout en restant compatible avec le rendu de textes et graphiques fixes ; il n'a pas été prévu avec ce que permet le post-traitement numérique avec les accélérateurs graphiques d'aujourd'hui, mais comme ces derniers peuvent effacer facilement les défauts du modèle sRGB, il n'est pas nécessaire de changer de modèle de référence (tant qu'on reste limité aux images trichromatiques ou monochromes).
- Quantification et arrondi
L'espace couleur sRGB permet d'arrondir à l'unité les valeurs exprimées sur 8 bits, de 0 à 255, la transition entre deux nuances étant moindre que la différence juste perceptible. Ce n'est pas le cas du codage vidéo analogique issu de l'ancienne norme ITU-R 709.BT qui s'appliquait aux moniteurs analogiques VGA et aux téléviseurs, pour éviter des distorsions de gamme lors de la reproduction sur moniteur numérique ou la codification standard des couleurs sRGB sur le web; pour la codification des formats vidéo numériques d'autres modèles colorimétriques permettent d'étendre directement la gamme sans cet ajustement et avec une valeur gamma moins élevée ; pour cela les moniteurs et écrans numériques comportent un réglage pour ajuster les vidéos converties en sRGB sur la même plage réduite que les systèmes analogiques avec un mode dit cinéma, ou bien d'utiliser la plage sRGB entière pour les applications informatiques, le web et la photographie numérique.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Commission internationale de l'éclairage, Norme 61966-2-1 (1999), (présentation en ligne)
- (en) Michael Stokes, Matthew Anderson, Srinivasan Chandrasekar et Ricardo Motta, A Standard Default Color Space for the Internet - sRGB, (lire en ligne)
- (en) « Proposal for a Standard Default Color Space for the Internet—sRGB » (consulté le ).
- (en) Sabine Süsstrunk, Robert Buckley et Steve Swen, « Standard RGB Color Spaces », 7th Color and Imaging Conference Final Program and Proceedings, Society for Imaging Science and Technology, , p. 127-134(8) (lire en ligne).
Liens externes[modifier | modifier le code]
- (en) International color Consortium, « sRGB », sur www.color.org (consulté le ) (voir aussi pdf)
- Daniel Metz, « Qu’est-ce que le sRGB ? », sur www.blog-couleur.com, (consulté le )
Références[modifier | modifier le code]
- Les valeurs numériques données ici sont celles de la spécification sRGB IEC 61966-2-1:1999.
- Les calculs supposent un observateur de référence CIE 2°.
- Le plus petit écart de couleur sur un écran conforme est supérieur à l'unité.
- « La télévision diffusée numériquement utilise une valeur codée 16 pour le noir et 235 pour le blanc, afin de permettre le rendu d'une plus large gamme de couleurs » (« Digital broadcast television uses a black digital count of 16 and a white digital count of 235 in order to provide a larger encoded color gamut »)[10].
- IEC 61966, p. 10.
- IEC 61966, p. 14 renvoie à Union internationale des télécommunications, UIT-R BT.709-5, (lire en ligne).
- IEC 61966, p. 10, 12.
- « ISO 16760:2014 Technologie graphique — Échange de données pré-impression — Préparation et visualisation d'images RGB à utiliser dans les flux de travail des arts graphiques basés sur le RGB », (consulté le ).
- Süsstrunk, Buckley et Swen 1999.
- Henri Maître, Du photon au pixel : L'appareil photographique numérique, ISTE, , p. 167.
- Maître 2016, p. 167-169 « 5.2.6 L'espace sRGB ».
- (en) Charles Poynton, « The rehabilitation of gamma », dans Human Vision and Elec-tronic Imaging III, (lire en ligne) [PDF].
- (en) Charles Poynton, Picture rendering, image state, and BT.709, (lire en ligne), p. 3 cite (en) I.G. Maloff, « Gamma and Range in Television », RCA Review, vol. 3, no 4, , p. 409–417.
- présentation de sRGB, 1996.



















