Produit matriciel de Hadamard
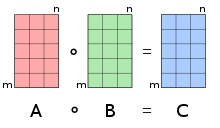
En mathématiques, le produit matriciel de Hadamard, nommé d'après le mathématicien français Jacques Hadamard et parfois désigné produit de Schur[1], est une opération binaire qui pour deux matrices de mêmes dimensions, associe une autre matrice, de même dimension, et où chaque coefficient est le produit terme à terme des deux matrices. En cela, il est à distinguer du produit matriciel usuel.
Le produit matriciel de Hadamard est associatif et distributif, et contrairement au produit matriciel classique, commutatif.
Définition[modifier | modifier le code]
Formellement, pour deux matrices de mêmes dimensions
le produit de Hadamard est une matrice
dont les coefficients sont
Propriétés[modifier | modifier le code]
- Le produit de Hadamard est commutatif, associatif et distributif sur l'addition :
- L'élément neutre pour le produit de Hadamard de deux matrices de taille m × n est une matrice m × n dont tous les éléments sont égaux à 1, contrairement à la matrice identité, qui est l'élément neutre du produit matriciel classique et dont les coefficients valent 1 sur la diagonale et 0 sinon. Ainsi, une matrice admet une inverse pour le produit de Hadamard si et seulement si tous ses éléments sont non nuls[2].
- , où MT (respectivement M*) désigne la matrice transposée (resp. la matrice adjointe) de M. En particulier, le produit de Hadamard de deux matrices n × n symétriques (resp. hermitiennes) est une matrice symétrique (resp. hermitienne).
- Si D est diagonale alors
- En notant ej le j-ème vecteur de la base canonique de ℂn et, pour tout vecteur x, Dx la matrice diagonale dont les éléments diagonaux sont les coordonnées de x, on remarque que l'élément d'indice i, j du produit de Hadamard est égal au i-ème élément diagonal de ADejBT :
On en déduit immédiatement : - Le produit de Hadamard est une sous-matrice principale du produit de Kronecker.
Théorème du produit de Schur[modifier | modifier le code]
Le produit de Hadamard de deux matrices n × n hermitiennes positives (resp. définies positives) est une matrice (n × n) hermitienne positive (resp. définie positive)[4]. C'est le théorème du produit de Schur[2] démontré pour la première fois[5] par Issai Schur[6].
Pour deux matrices hermitiennes positives A et B, on a aussi
Applications[modifier | modifier le code]
Le produit de Hadamard est utilisé en compression de données comme le JPEG.
Il est également utilisé en apprentissage automatique dans la formalisation de certains modèles, notamment dans le cadre des réseaux de neurones artificiels.
Références[modifier | modifier le code]
- (en) Roger A. Horn et Charles R. Johnson, Matrix Analysis, CUP, , 561 p. (ISBN 978-0-521-38632-6, lire en ligne), chap. 5.
- (en) Elizabeth Million, « The Hadamard Product ».
- (en) Roger A. Horn et Charles R. Johnson, Topics in Matrix Analysis, CUP, , 607 p. (ISBN 978-0-521-46713-1, lire en ligne), p. 306.
- (en) George P. H. Styan, « Hadamard Products and Multivariate Statistical Analysis », Linear Algebra and its Applications, vol. 6, , p. 217-240 (DOI 10.1016/0024-3795(73)90023-2).
- Horn et Johnson 1991, p. 309.
- (de) J. Schur, « Bemerkungen zur Theorie der beschränkten Bilinearformen mit unendlich vielen Veränderlichen », J. reine angew. Math., vol. 140, , p. 1-28 (DOI 10.1515/crll.1911.140.1), p. 14, théorème VII.
- (en) Denis Serre, Matrices : Theory and Applications, Springer, coll. « GTM » (no 216), (lire en ligne), p. 123.















