Perspective isométrique

La perspective isométrique est une méthode de représentation en perspective dans laquelle les trois directions de l'espace sont représentées avec la même importance, d'où le terme.
C'est un cas particulier de perspective axonométrique.
Principe[modifier | modifier le code]

En géométrie analytique, on définit un repère orthonormé.
La perspective isométrique correspond à une vue selon la droite dont un vecteur directeur a pour coordonnées dans ce repère. Ainsi, un cube dont les arêtes suivent les axes du repère se voit selon sa grande diagonale, comme un hexagone.
Les axes se projettent donc sur un plan perpendiculaire à cette grande diagonale. Les longueurs subissent une réduction (la projection est une isométrie, le facteur de réduction est le même pour toutes les longueurs sur un axe donné).
C'est une perspective qui est facile à exécuter dans le cas de formes simples. C'est une approximation de la vue « réelle », qui est satisfaisante tant que la profondeur reste faible : en particulier elle ne prend pas en compte la réduction apparente de taille avec l'éloignement.
Elle est très utilisée pour la représentation normalisée des tuyauteries ; on ne représente que l'axe des tuyaux sans s'intéresser à l'échelle. Les tuyauteurs utilisent un document, la « trame iso », avec un quadrillage reprenant les directions des axes.
Règles de base pour dessiner en perspective isométrique[modifier | modifier le code]
Les mesures[modifier | modifier le code]

On parle de perspective isométrique car les distances sont reportées de la même manière sur les trois axes. On applique à toutes les longueurs qui sont colinéaires à un axe un coefficient réducteur de 0,82.
Dans le cas de la représentation d'un objet, on définit d'abord une face de l'objet que l'on considère comme la face avant, et l'on y place un repère ; dans ce plan, on n'a donc que deux axes visibles, le troisième est perpendiculaire au dessin. L'origine du repère est en général placée dans un coin.
On réalise ensuite deux vues (au moins) qui sont les projections orthogonales de l'objet sur la face avant et sur une face perpendiculaire (face de gauche, de droite, du dessus ou du dessous). Ensuite, il suffit de mesurer les coordonnées des points dans ce repère à partir des deux figures, et de reporter ces coordonnées sur les axes de la perspective isométrique en appliquant ce coefficient de 0,82.
Les angles[modifier | modifier le code]
Les angles entre les axes (x, y et z) sont tous égaux (120°).
Les cercles[modifier | modifier le code]
Les cercles sont des formes importantes dans le dessin technique ; ceci est une conséquence des procédés de fabrication des pièces (usinage) : perçage, fraisage, tournage, etc. Ils sont aussi importants en génie civil (débouchés de tuyaux, arc en plein-cintre, giratoires, etc. Lorsque l'on génère la perspective isométrique par ordinateur, celui-ci peut calculer la transformation du cercle. Mais ceci devient compliqué lorsque l'on dessine à la main.
Remarquons dans un premier temps qu'un cercle est toujours inscrit dans un carré auquel il est 4 fois tangent, au milieu des côtés. En vue de face, on contraint donc le cercle dans un carré.
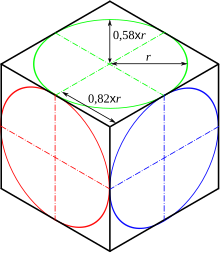
En perspective isométrique, ce carré devient un parallélogramme. Les tangences restent les mêmes (milieu des côtés), mais le cercle devient une ellipse.
La projection oblique fait varier le diamètre du cercle entre 1 (grand diamètre de l'ellipse, donc diamètre horizontal du cercle de départ projeté en vraie grandeur) et 0,58 (son petit diamètre, vu sous sa plus importante réduction dans la direction de la plus grande pente).
Des trace-ellipses normalisés permettent de tracer des ellipses respectant ces proportions pour plusieurs tailles de grand axe.
Défauts et limites de la perspective isométrique[modifier | modifier le code]


Comme toutes les projections et toutes les perspectives, la perte de la troisième dimension induit des erreurs possibles d'interprétation. Ceci a été abondamment utilisé par l'artiste M. C. Escher pour créer des situations impossibles.
En l'occurrence, un déplacement de 1 cm sur l'axe z se traduit graphiquement de la même manière qu'un déplacement de 1 cm selon l'axe des x et des y, soit un déplacement de √2 ≈ 1,41 selon la bissectrice de l'angle droit formé par les axes x et y.
Utilisations de la perspective isométrique[modifier | modifier le code]
Utilisation en dessin technique[modifier | modifier le code]

En dessin industriel, on représente une pièce sous différents angles de vue, perpendiculairement à des axes. Ces axes sont « naturels » : une pièce ayant une fonction mécanique (liaison et mouvement avec d'autres pièces), elle présente des contraintes de forme et d'usinage qui font qu'elle a en général un axe de symétrie ou des faces planes. Ces axes ou les arêtes de ces faces permettent de définir un repère orthogonal (que l'on choisit orthonormé).
On peut donc facilement exécuter une perspective isométrique d'une pièce à partir des vues en géométrie descriptive utilisées habituellement.
La perspective isométrique permet au lecteur de se représenter facilement la forme de la pièce, mais ne permet pas de transmettre des informations utiles à la conception et à la réalisation de la pièce.
Utilisation en architecture[modifier | modifier le code]
Eugène Viollet-le-Duc l'a utilisée dans plusieurs de ses tableaux de châteaux (et de leurs bâtiments annexes) pour éviter d'accentuer l'importance de certains de ces éléments et de la position de l'observateur (le cavalier de la perspective cavalière dans l'observation des fortifications).
Utilisation dans les jeux vidéo[modifier | modifier le code]

Un certain nombre de jeux vidéo (comme Zaxxon, Marble Madness, Monument Valley, Crafton et Xunk ou encore Project Zomboid) mettant en œuvre des personnages utilisent une vue objective en perspective isométrique ; on parle souvent, dans ce domaine, de « perspective 3/4 ». D'un point de vue pratique, cela permet de déplacer les éléments graphiques (sprites) sans en changer la taille, ce qui était indispensable lorsque les ordinateurs étaient peu puissants, et présente toujours un grand intérêt pour les consoles de poche.
Cela pose cependant quelques problèmes de confusion (du fait de l'aplatissement de l'image, la profondeur est rendue par un déplacement dans le plan).
En raison de la pixellisation, et dans un souci d'optimisation des calculs, certains jeux font progresser les axes selon un rapport de 2:1, ceux-ci sont donc inclinés d'un angle de 26,6° (arctan 0,5) au lieu de 30°. Ce n'est donc pas de la perspective isométrique à proprement parler, mais une perspective dimétrique (un autre type de perspective axonométrique), mais le terme « isométrique » est cependant utilisé par abus de langage.
Approche mathématique[modifier | modifier le code]
La perspective isométrique est en fait une projection sur un plan selon un axe orthogonal à ce plan : une projection orthogonale. C'est une application linéaire.
Facteur de report sur les axes[modifier | modifier le code]

On peut calculer le facteur de proportionnalité sur les axes simplement grâce à la trigonométrie :
- considérons l'arête du cube qui va de l'origine au point (0,0,1) ; elle fait un angle α avec le plan de projection, le projeté a donc une longueur de cos α ;
- α est aussi l'angle entre la normale au plan de projection passant par l'origine et par le point (1,1,1), et la bissectrice des axes x et y qui passe par (1,1,0) ;
- dans le triangle formé par les points (0,0,0), (1,1,0) et (1,1,1) est un triangle rectangle ; le segment [(0,0,0), (1,1,0)] a pour longueur √2 (diagonale du carré), le segment [(1,1,0), (1,1,1)] a pour longueur 1, et l'hypoténuse [(0,0,0), (1,1,1)] a pour longueur √3
On a donc
- .
On en déduit que α ≈ 35,26 °.
On peut aussi utiliser le produit scalaire :
- le vecteur unitaire porté par la grande diagonale est (1/√3, 1/√3, 1/√3) ;
- l'arête [(0,0,0), (0,0,1)] se projette sur la grande diagonale en un segment de longueur k1, et sur le plan normal à cette grande diagonale en un segment de longueur k2
- k1 est le produit scalaire de et de , et peut se calculer avec les coordonnées :
- le théorème de Pythagore nous indique que k12 + k22 = 1 (longueur de l'arête du cube).
On a donc :
- .
Les longueurs des segments sur les axes du repère se projettent donc avec un facteur de 0,82.
On arrive également à cette conclusion en utilisant la formule générale des projections orthogonales, voir Perspective axonométrique > Perspective isométrique.
Par ailleurs, si l'on considère le cercle unité du plan (x, y), le rayon se projetant selon la ligne de plus grande pente est la première bissectrice du plan, avec un facteur de projection valant sin α = k1 = 1/√3 ≈ 0,58, ce qui correspond au petit axe de l'ellipse.
Transformation des coordonnées[modifier | modifier le code]

La transformation des coordonnées cartésienne est utilisée pour calculer les vues à partir des coordonnées des points, par exemple dans le cas de jeux vidéo ou de logiciels de représentation graphique 3D.
Supposons l'espace muni d'une base orthonormée directe . La projection P se fait selon le vecteur de composantes , c'est-à-dire le vecteur , selon le plan représenté par ce même vecteur.
Comme toute application linéaire, elle peut être représentée par la transformation des vecteurs de la base, puisqu'un vecteur quelconque se transforme selon
- .
Soit . Appelons la base orthonormée directe dans le plan de projection. On choisit arbitrairement que fait un angle de -π/6 avec .
L'application des calculs pour les projections orthogonales au cas particulier de la perspective isométrique nous donne (voir Perspective axonométrique > Perspective isométrique) :
- ; ;
- ; ;
- ; .
La matrice de la projection MP est donc
- .
Considérons un point (x, y, z) de l'espace qui se projette en (x', y'). Sa projection sera donc :
- .
Voir aussi Projection (géométrie) > Projection sur un plan parallèlement à une droite en géométrie analytique.
Transformation d'un cercle d'un plan contenant deux axes[modifier | modifier le code]
Considérons le cercle trigonométrique du plan . Les coordonnées paramétriques de ses points sont :
Les coordonnées des points projetés dans la base sont donc
La distance à l'origine est , soit
(formule de Moivre) ; ceci fournit au passage une équation paramétrique de l'ellipse. Cette distance varie donc entre 1 et . On retrouve les rapports du grand axe et du petit axe de l'ellipse.





























