Inégalité de Young

En mathématiques, la forme standard de l'inégalité de Young, portant le nom de William Henry Young, affirme que pour tous réels a et b positifs ou nuls et tous réels p et q strictement positifs tels que 1/p + 1/q = 1 (on dit parfois qu'ils sont conjugués), on a :

$ab\leqslant {\frac {a^{p}}{p}}+{\frac {b^{q}}{q}}.$

L'égalité a lieu si et seulement si a^p = b^q.

Un cas simple (relativement fréquemment utilisé) de l'inégalité de Young est l'inégalité avec exposants 2 :

$ab\leqslant {\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}$

qui donne également l'inégalité de Young avec ε (valide pour tout ε > 0) :

$ab\leqslant {\frac {a^{2}}{2\varepsilon }}+{\frac {\varepsilon b^{2}}{2}}.$

Utilisation

L'inégalité de Young peut être utilisée dans la preuve de l'inégalité de Hölder. Elle est également largement utilisée pour estimer la norme de termes non linéaires en théorie des équations aux dérivées partielles, puisqu'elle permet d'estimer un produit de deux termes par une somme des deux mêmes termes à une puissance quelconque et divisé par un nombre.

Démonstrations

Cas élémentaire

L'inégalité de Young avec des exposants 2 est le cas particulier p = q = 2. Mais elle a une preuve plus élémentaire : on observe seulement que

$0\leqslant (a-b)^{2}=a^{2}+b^{2}-2ab,$

on ajoute $2ab$ de chaque côté et on divise par 2.

L'inégalité de Young avec ε suit, en appliquant l'inégalité de Young avec exposants 2 à

$a'=a/{\sqrt {\varepsilon }},\quad b'={\sqrt {\varepsilon }}b.$

Forme standard

La forme standard est l'inégalité entre moyennes pondérées arithmétique et géométrique, appliquée à $n=2,x_{1}=a^{p},x_{2}=b^{q},\alpha _{1}=1/p,\alpha _{2}=1/q$, mais se déduit aussi de la section suivante.

Généralisation utilisant des intégrales

L'aire du rectangle (ab) ne peut dépasser la somme des aires correspondant à l'intégrale de la fonction $f$ (en rouge) et de la fonction $f^{-1}$ (en jaune).

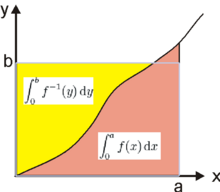
L'inégalité ci-dessus est un cas particulier de la suivante, démontrée par Young :

Soit $f$ une fonction continue strictement croissante sur $[0,c]$ (avec $c>0$) et $f^{-1}$ sa bijection réciproque. Si $f(0)=0$, $a\in [0,c]$ et $b\in [0,f(c)]$ alors

$ab\leqslant \int _{0}^{a}f(x)\,\mathrm {d} x+\int _{0}^{b}f^{-1}(y)\,\mathrm {d} y$,

avec égalité si et seulement si $b=f(a)$.

Le diagramme ci-contre donne une preuve graphique très simple de ce résultat, en interprétant les deux intégrales comme deux aires bordées par le graphe de $f$.

Le calcul précédent revient à dire que si F est une fonction strictement convexe de classe C¹ alors, en notant G sa transformée de Legendre (ou fonction conjuguée),

$ab\leqslant F(a)+G(b).$

Sous cette forme, cette inégalité est encore valide si F est une fonction convexe à argument vectoriel.

Pour des détails, voir Mitroi&Niculescu .

Exemples d'applications

• La transformée de Legendre de $F(a)=a^{p}/p$ est $G(b)=b^{q}/q$ avec $q$ tel que 1/p + 1/q = 1, et ainsi l'inégalité de Young standard est un cas particulier de l'inégalité ci-dessus.
• La transformée de Legendre de $F(a)={\text{e}}^{a}$ est $G(b)=b\ln b-b$, et alors $ab\leqslant e^{a}+b\ln b-b$ pour tous $a$ et $b$ strictement positifs.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Young inequality » (voir la liste des auteurs).