Taux d'expansion (théorie des graphes)
En mathématiques, et plus particulièrement en théorie des graphes, le taux d'expansion d'un graphe est une mesure de connectivité de ce graphe[1]. Informellement, un grand taux d'expansion veut dire que n'importe quel sous-ensemble de sommets relativement petit possède beaucoup de connexions avec le reste du graphe.
Cette mesure est surtout utilisée en raison des propriétés intéressantes des graphes ayant un fort taux d'expansion, parfois appelés graphes expanseurs. On les retrouve notamment en informatique théorique.
Définitions[modifier | modifier le code]

Frontière d'une partie du graphe[modifier | modifier le code]
Soit un graphe non orienté à sommets et un sous-ensemble de sommets de . On appelle frontière[2] (boundary) de , notée , l’ensemble des arêtes de partant d'un sommet de et n'aboutissant pas à un sommet de . En notation mathématique, cela donne :
- .
Notons que l'ensemble peut aussi être défini comme la coupe entre et . Cette frontière est définie comme un ensemble d'arêtes[3], on parle parfois de frontière des arêtes (edge boundary) pour la différencier des notions de frontières des sommets (vertex boundaries) :
- la frontière des sommets extérieure (outer vertex boundary)[4] notée est définie comme l'ensemble des sommets de ayant au moins un voisin dans :
- ;
- la frontière des sommets intérieure (inner vertex boundary)[4] notée est définie comme l'ensemble des sommets de ayant au moins un voisin dans :
- .
Sur la figure, la frontière intérieure est en vert entouré en beige et la frontière extérieure en noir entouré en beige.
Taux d'expansion[modifier | modifier le code]
Le taux d'expansion[1] du graphe non orienté est :
- .
En d'autres termes, est le minimum, pris sur des parties comportant au maximum sommets, du rapport entre le nombre d'arêtes de la frontière de et le nombre de sommets de .
est aussi appelé nombre isopérimétrique (isoperimetric number) ou constante de Cheeger, sachant qu'il existe aussi une constante de Cheeger en géométrie riemannienne[réf. nécessaire].
On remarque que est calculé sur le nombre d'arêtes s'échappant de et non pas sur le nombre de sommets juste à l'extérieur de . Cela ne donne pas toujours la même valeur : deux arêtes issues de deux sommets différents de peuvent aboutir au même sommet de . On précise donc qu'il s'agit du taux d'expansion des arêtes (edge expansion).
On peut aussi définir des taux d'expansion des sommets (vertex expansion)[4] :
- ;
- .
On a les relations :
où est le degré maximal du graphe.
Graphe expanseur[modifier | modifier le code]
Soit un graphe non orienté à sommets. Le graphe est un graphe expanseur[5] de facteur si, pour tout sous-ensemble de sommets de cardinal , on a . On dit aussi que le graphe est -expanseur. Certains auteurs imposent dans la définition un degré maximal aux sommets du graphe[6], afin qu'il reste creux (le graphe complet n'a en effet vraiment pas de mérite à être fortement connecté).
On remarque que : le taux d'expansion est la meilleure valeur pour .
Tout graphe connexe à sommets est -expanseur : il existe toujours au moins une arête pour s'échapper d'une partie du graphe, sinon il ne serait pas connexe.
Historique et applications[modifier | modifier le code]
La notion de graphe expanseur et de taux d'expansion remonte aux années 1970[2]. La motivation initiale était de construire des réseaux (téléphoniques ou informatiques) robustes.
En mathématiques, on retrouve cette notion pour graphes de Cayley de certains groupes de matrices et dans la conjecture de Baum-Connes. On la rencontre aussi dans les taux de convergence des chaînes de Markov et dans l'étude des algorithmes de Monte-Carlo. Enfin, elle joue un rôle dans le problème isopérimétrique[1].
On utilise les graphes à fort taux d'expansion en informatique théorique pour construire des familles de codes correcteurs d'erreur[7]. Ils sont aussi utilisés pour des preuves en théorie de la complexité, notamment pour la preuve d'Irit Dinur du théorème PCP et la preuve d'Omer Reingold que L=SL. Ils sont aussi liés aux aspects probabilistes de l'informatique.
Encadrement du taux d'expansion dans le cas des graphes réguliers[modifier | modifier le code]
Il est difficile de calculer directement le taux d'expansion d'un graphe, du moins dans le cas général. En effet, le nombre de parties de ce graphe comportant moins de la moitié des sommets croît rapidement en fonction du nombre de sommets et on a du mal à examiner tous les cas. Il est donc intéressant de disposer d'un encadrement de cette valeur.
Rappelons que la matrice d'adjacence d'un graphe non orienté est symétrique et qu'elle est donc à valeurs propres réelles. Par ailleurs, pour un graphe d-régulier (i.e. un graphe où tous les sommets ont le même nombre d de voisins), la plus grande valeur propre est le degré d du graphe. Le résultat suivant est dû à J. Cheeger, P. Buser, J. Dodziuk, N. Alon et V. D. Milman[1] :
Théorème — Soit la matrice d'adjacence d'un graphe -régulier. Soit sa deuxième plus grande valeur propre. Alors le taux d'expansion du graphe vérifie .
La quantité est appelée trou spectral (spectral gap).
Exemples[modifier | modifier le code]
Graphe non connexe[modifier | modifier le code]

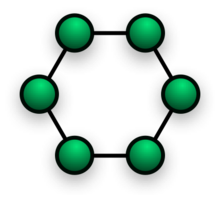
Considérons le graphe 2-régulier à 6 sommets G ci-contre (n = 6, d = 2).
En regardant le graphe, on voit que, pour une partie W égale à l'un des deux groupements de 3 sommets, il n'y a aucune arête qui parte vers un sommet de l'autre groupement. Le taux d'expansion h(G) vaut 0 et le graphe n'est pas expanseur.
La matrice d'adjacence correspondant au graphe est :
Le calcul montre que les deux plus grandes valeurs propres sont toutes deux égales à 2. Ce n'est pas étonnant, un graphe est non connexe si et seulement si les deux plus grandes valeurs propres de la matrice d'adjacence sont égales.
On en déduit :
Par conséquent, : on retrouve bien que h(G) vaut 0.
Graphe de Petersen[modifier | modifier le code]

Considérons le graphe 3-régulier à 10 sommets G ci-contre (n = 10, d = 3).
Numérotons les sommets en tournant deux fois, la première fois autour du pentagone extérieur, la deuxième fois autour de l'étoile intérieure. Avec cette numérotation, la matrice d'adjacence est :
Le calcul montre que les deux plus grandes valeurs propres de cette matrice sont 3 et 1.
On en déduit :
Par conséquent, .
En fait, . Pour s'en persuader, il suffit de considérer les 5 sommets de l'étoile centrale : il n'y a que 5 arêtes qui s'en échappent, ce qui correspond à un rapport arêtes de la frontière divisé par le nombre de sommets égal à 1.
Graphe cycle[modifier | modifier le code]
Considérons le graphe 2-régulier à n sommets G ci-contre (n pair et variable, d = 2).
Considérons une partie W de V de moins de n / 2 sommets :
- dans le « meilleur » des cas, les sommets de W sont éloignés les uns des autres, et il part deux arêtes de chaque sommet ;
- dans le « pire » des cas, les sommets de W sont tous regroupés d'un côté du graphe, et il n'y a que deux voies de sortie de cet ensemble.
Le minimum du rapport est atteint pour la plus grande valeur du nombre de sommets de W, c'est-à-dire n / 2.
On en déduit que .
Quand le nombre de sommets augmente, cette valeur tend vers 0, c'est un cas de goulot d'étranglement.
Graphe biparti complet[modifier | modifier le code]

Considérons le graphe d-régulier à 2 d sommets G ci-contre (n = 2 d).
Dans un graphe biparti complet, les valeurs propres de la matrice d'adjacence sont . On a donc et par conséquent .
En fait, si d est pair, on a . Pour le montrer, dans le dessin ci-contre, considérons l'ensemble des sommets rouges. On constate que arêtes (vertes) s'échappent de chacun des sommets rouges vers les sommets bleus et . Attention, ce n'est plus vrai si d est impair.
Pour d = 4 comme dans l'illustration ci-contre, on a h(G) = 2.
Graphe complet[modifier | modifier le code]
On considère le graphe d-régulier à d + 1 sommet où chaque sommet est connecté à tous les autres.
Cette fois, les valeurs propres de la matrice d'adjacence sont . On a donc et par conséquent , comme dans le cas précédent.
De fait, pour d impair et pour d pair.
Comme il a déjà été signalé dans la définition, des graphes denses comme le graphe biparti complet et le graphe complet n'ont pas vraiment de mérite à être fortement expanseurs, et certains auteurs les rejettent en imposant un degré maximum au graphe.
Famille de graphes expanseurs[modifier | modifier le code]
Il est intéressant de considérer non un graphe isolé, mais toute une famille de graphes.
Définition[modifier | modifier le code]
On dit qu'une famille infinie de graphes réguliers est une famille d'expanseurs s'il existe une constante telles que pour chaque [1]. Autrement dit, chaque graphe de la famille est expanseur dans un facteur .
Tous les auteurs s'accordent dans cette définition sur le fait qu'elle ne s'applique qu'aux graphes réguliers, mais on aurait pu imaginer qu'elle s'applique indifféremment à n'importe quelle famille de graphes.
Plusieurs auteurs demandent également que le degré d du graphe soit constant d'un membre de la famille à l'autre[2], mais il peut être intéressant d'avoir un degré qui évolue en fonction du nombre de sommets du graphe.
Non-exemple[modifier | modifier le code]
La famille des graphes cycles n'est pas une famille d'expanseurs, puisque le taux d'expansion d'un graphe cycle tend vers 0 quand le nombre de sommets tend vers l'infini. Le fait que chacun des membres de la famille, pris individuellement, soit un graphe expanseur dans un facteur 4/n ne suffit pas.
Construction explicite et exemple des graphes de Margulis[modifier | modifier le code]
Les familles d'expanseurs à d constant sont relativement difficiles à construire explicitement, et il est tout aussi malaisé de prouver qu'il s'agit effectivement de familles d'expanseurs et de calculer la constante correspondante. Gregori Margulis a exhibé la première de ces constructions en 1973, et c'est resté l'une des plus connues.
Description des graphes de Margulis[modifier | modifier le code]
- les sommets du graphe Gm sont des paires d'entiers entre 0 et m - 1 ;
- les voisins du sommet (x, y) sont au nombre de 8 : (x + y, y), (x - y, y), (x, y + x), (x, y - x), (x + y + 1, y), (x − y + 1, y), (x, y + x + 1) et (x, y − x + 1), toutes ces opérations étant modulo m.
Par exemple, dans le graphe G9, le sommet (3, 4) a pour voisins (7, 4), (8, 4), (3, 7), (3, 1), (8, 4), (0, 4), (3, 8) et (3, 2).
Il s'agit là d'une famille d'expanseurs telle que pour chacun des graphes de la famille[8].
Preuve et lien avec les graphes de Cayley de groupes linéaires[modifier | modifier le code]
La preuve originelle de Margulis de l'expansion de la famille de graphes ci-dessus repose sur le fait que ces graphes sont des graphes de Cayley des quotients du groupe par des sous-groupes d'indice fini, et que le groupe a la propriété (T) de Kazhdan. Un autre exemple (qui donne des graphes plus compliqués) d'application de cette méthode est l'ensemble des graphes de Cayley des groupes par rapport aux images d'une partie génératrice fixée de , pour parcourant les nombres premiers. Un autre exemple plus simple du même genre est celui des graphes de Cayley des groupes par rapport aux générateurs pour (dans ce cas la preuve de l'expansion repose sur une propriété plus subtile que la propriété (T))[9].
L'expansion des quotients de groupes linéaires finiment engendré a été récemment le focus d'un important effort de recherche. Le théorème le plus général dans cette direction est le suivant[10] (en fait un cas particulier du résultat principal de cette référence).
Soit un sous-groupe de engendré par une partie finie . Il existe un entier tel que , et pour un nombre premier on a donc une application bien définie . On suppose que le groupe est Zariski-dense. Alors les graphes de Cayley des groupes finis pour les ensembles générateurs forment une famille d'expanseurs.
Un exemple (qui prédate le travail de Salehi-Golsefidy et Varju) est le suivant : l'ensemble des graphes de par rapport aux générateurs pour premier. Noter que contrairement à l'exemple ci-dessus les matrices n'engendrent pas un sous-groupe d'indice fini dans , ce qui rend la preuve de l'expansion nettement plus difficile.
L'intérêt de ces exemples vient de problèmes de la théorie des nombres[11].
Notes et références[modifier | modifier le code]
- (en) Shlomo Hoory, Nathan Linial et Avi Widgerson. Expander graphs and their applications, an overview, Bulletin of the American Mathematical Society, volume 43, no 4, octobre 2006, p. 439-561
- F. Jouve, Graphes à taux d'expansion optimal
- Chez la plupart des auteurs, les arêtes de la frontière sont des arêtes orientées, bien que le graphe de départ soit non orienté. La définition donnée ici est simplifiée.
- (en) S. Bobkov, C. Houdré et P. Tetali, « λ∞, vertex isoperimetry and concentration », Combinatorica, vol. 20, no 2, , p. 153–172 (lire en ligne).
- (en) Oded Goldreich, Basic facts about expander graphs
- (en) Ho Yee Cheung, Lap Chi Lau, Kai Man Leung, Graph Connectivities, Network Coding, and Expander Graphs, Université chinoise de Hong Kong, août 2011
- (en) Spielman (D.A.). Computationally efficient error-correcting codes and holographic proofs, Massachusetts Institute of Technology, thèse de PhD, mai 1995.
- (en) José Miguel Pérez Urquidi, Expander graphs and error correcting codes, thèse de master, Université de Bordeaux 1, juillet 2010.La référence ne prouve pas cette majoration, mais une valeur plus faible.[réf. non conforme]
- (en) Alex Lubotzky, Discrete groups, expanding graphs and invariant measures, Birkhäuser, .
- (en) Alireza Salehi-Golsefidy et Peter Varju, « Expansion in perfect groups », GAFA, vol. 22, no 6,
- (en) Alireza Salehi-Golsefidy, « Affine sieve and expanders », in Thin Groups and Superstrong Approximation, (Editors: H. Oh, E. Breuillard), MSRI publication 61, Cambridge University Press 2014
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Jeff Cheeger, A lower bound for the smallest eigenvalue of the Laplacian. Problems in analysis, pages 195–199. Princeton Univ. Press, 1970.
- (en) Gregori Margulis, Explicit constructions of expanders. Problemy Peredači Informacii, 1973.






































































![{\displaystyle \Gamma \subset \mathrm {SL} _{n}(\mathbb {Z} [1/N])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f069a646a37b3bf5f7fc031bb4cf2024985065c6)






