Propulsion spatiale

La propulsion spatiale comprend tout système permettant d’accélérer un objet dans l'espace. Cela inclut les moyens de propulsion des véhicules spatiaux (fusées, satellites, sondes) ou les systèmes de commande d'attitude et d'orbite.
Différentes méthodes de propulsion spatiale existent, chacune ayant ses défauts et ses avantages. La propulsion spatiale est un domaine de recherche actif, pourtant la plupart des véhicules spatiaux utilisent actuellement le même type de propulsion s'appuyant sur l'éjection de gaz à grande vitesse en arrière du véhicule au travers d'une tuyère. Ce genre particulier de propulsion est appelé moteur-fusée.
La plupart des vaisseaux spatiaux actuels utilisent des moteurs-fusées chimiques (à propergol solide ou à ergols liquides) pour le lancement même si certains systèmes (comme le lanceur Pegasus ou le vaisseau SpaceShipOne) ont recours partiellement à un lancement aéroporté. La plupart des vaisseaux spatiaux utilisent un système de propulsion chimique simple mais fiable mono-ergol ou un système de propulsion électrique pour le maintien à poste. Des actionneurs gyroscopiques ou roues d'inertie peuvent également être utilisés pour le contrôle d'attitude. Les satellites soviétiques utilisent la propulsion électrique depuis des décennies, une technologie qui commence seulement à devenir fréquente dans les pays occidentaux en particulier pour le maintien à poste nord-sud des satellites géostationnaires et la rehausse de leur orbite. Les sondes interplanétaires utilisent pour la plupart des moteurs chimiques, cependant quelques essais d'utilisation de moteur ionique (Dawn et Deep Space 1) ou à effet Hall ont démontré leur efficacité.
Besoin[modifier | modifier le code]
Les satellites artificiels doivent être placés sur orbite de manière précise par un lanceur. Une fois sur leur orbite, ils doivent la plupart du temps contrôler leur attitude de manière à être correctement pointés vers la Terre, le Soleil ou d'autres astres dans le cas de missions astronomiques[1]. Les satellites en orbite autour d'astres comportant une atmosphère doivent également compenser la traînée provoquée par l'atmosphère résiduelle. Il est ainsi nécessaire d'effectuer des petites corrections d'orbite régulièrement pour pouvoir rester sur orbite basse pour une longue période[2]. Beaucoup de satellites modifient également leur orbite au cours de leur mission pour remplir leurs objectifs ce qui demande également un système de propulsion spatiale. Ces changements dépendent des besoins[3]. Dans la plupart des cas, la fin des réserves de carburant du système propulsif est synonyme de fin de vie pour l'engin spatial. Si cette fin de vie reste majoritaire, une nouvelle tendance de prolongation de fonctionnement commence à voir le jour. Le , un satellite, MEV-1, s’est amarré pour la première fois à un autre satellite, Intelsat-901, en orbite géostationnaire. MEV-1 pour Mission Extension Vehicle-1 (véhicule d’extension de mission) est conçu pour accoster des satellites géostationnaires dont le carburant est presque épuisé. Une fois connecté à son satellite client, il utilise ses propres propulseurs et son approvisionnement en carburant pour prolonger la durée de vie du satellite[4].
Les engins spatiaux qui voyagent au-delà de l'orbite terrestre ont également besoin de se propulser dans l'espace. Une fois lancé depuis la Terre comme les satellites habituels, ces vaisseaux interplanétaires doivent utiliser un système de propulsion pour quitter l'orbite terrestre et naviguer dans le Système solaire. Les sondes spatiales corrigent habituellement leur trajectoire par de petits ajustements successifs au cours de leur croisière[5]. Durant le transit entre deux planètes les sondes poursuivent leur trajectoire sans propulsion. La trajectoire la plus efficace en termes de propulsion entre deux orbites elliptiques sur un même plan est appelée orbite de transfert de Hohmann. Partant d'une orbite circulaire, une courte poussée dans la direction de son mouvement entraîne le vaisseau sur une orbite elliptique. Une autre poussée à l'apoapside permet de retrouver une deuxième orbite circulaire, d'altitude plus élevée, où il accélère à nouveau pour sortir de l'orbite, complétant ainsi le transfert[6]. Certaines méthodes exotiques comme l'aérofreinage sont parfois utilisées pour réaliser les ajustements finaux d'une trajectoire[7].

Certaines méthodes de propulsion comme les voiles solaires produisent une poussée très faible mais continue[8]. Un véhicule interplanétaire utilisant de tels systèmes de propulsion ne peut utiliser une orbite de transfert de Hohmann, basé sur le caractère impulsionnel de l'accélération donnée en début et en fin de transfert. Par conséquent les systèmes propulsifs de faible poussée utilisent des stratégies complexes de direction de la poussée. Le concept de voile solaire a été démontré par le projet japonais IKAROS.
Les vaisseaux interstellaires auront besoin d'autres méthodes de propulsion. Aucun vaisseau de ce type n'a été construit même si de nombreux concepts ont été proposés. Les distances astronomiques séparant les étoiles entre elles requièrent des vitesses très importantes pour que le voyage se déroule dans des délais raisonnables. Accélérer à de telles vitesses puis ralentir à l'approche de la destination sera un défi pour les concepteurs de tels vaisseaux[9].
La force de gravité à la surface de la Terre est relativement élevée. La vitesse nécessaire pour pouvoir quitter le champ d'influence gravitationnelle de la Terre est environ de 11,2 km/s. Les humains étant habitués à une accélération gravitationnelle de 1 g soit environ 9,8 m s−2, un système de propulsion idéal pour simuler les conditions de gravité terrestre accélérerait donc à 1 g. Le corps humain supporte néanmoins des accélérations plus fortes pour des périodes de temps réduites. Cette gravité artificielle permettrait en outre de résoudre les problèmes liés à la micropesanteur comme la nausée ou les pertes osseuses et musculaires.
Méthodes de propulsion[modifier | modifier le code]
Les méthodes de propulsion spatiale peuvent être classées en fonction de la façon dont elles accélèrent la masse propulsive. Il existe également des méthodes particulières dépendant des phases du vol, comme le lancement, la rentrée ou encore l’atterrissage.
Moteur à réaction[modifier | modifier le code]

Un moteur à réaction utilise l'expulsion d'une masse propulsive pour assurer son déplacement, cela en s'appuyant sur la troisième loi de Newton.
Impulsion spécifique et vitesse d'éjection[modifier | modifier le code]
L'objectif d'un système de propulsion spatiale est d'accroître la vitesse v d'un engin spatial. Accélérer un objet est d'autant plus difficile que sa masse est importante ; aussi la quantité de mouvement, ou impulsion, p = m v, plutôt que la vitesse est utilisée pour caractériser ce phénomène. Ce qu'on appelle couramment dans le domaine du spatial une "impulsion" est en fait une variation de la quantité de mouvement[10].
Si le système de propulsion est utilisé dans le cadre d'un lancement, la poussée (donc une force) qu'il développe doit dépasser le poids du vaisseau afin que la résultante d'accélération soit positive[11]. Par contre, une fois en orbite, toute poussée, aussi faible soit-elle, provoquera une variation de la quantité de mouvement.
La modification de la quantité de mouvement au cours du temps est une force (principe fondamental de la dynamique) tandis qu'une accélération est une modification de la vitesse au cours du temps. Pour modifier sa vitesse, un vaisseau peut, soit maintenir une accélération faible sur une longue période, soit accélérer fortement sur une courte durée. De la même manière, pour modifier sa quantité de mouvement, le vaisseau peut subir une faible poussée pendant longtemps, ou une forte poussée pendant une courte durée. Cela implique que, lors de manœuvres dans l'espace, une méthode de propulsion qui provoque une faible accélération pendant longtemps permet d'obtenir la même variation de quantité de mouvement qu'une méthode de propulsion provoquant une forte accélération pendant un temps court. À nouveau, si le vaisseau lutte contre la gravité de la planète (s'il en décolle, par exemple), une poussée au moins égale à la gravité est nécessaire.
Si certains systèmes de propulsion spatiale utilisent des champs magnétiques ou la lumière comme intermédiaire dans cette transmission de quantité de mouvement, la plupart communiquent une quantité de mouvement à une masse éjectée dans le sens inverse de la poussée.
Le bilan de quantité de mouvement s'écrit pour l'engin :
où dP est variation de quantité de mouvement et ve la vitesse d'éjection de la matière.
Cette variation se traduit, en utilisant la deuxième loi de Newton appliquée sur l'engin, par une force s'exerçant sur l'engin :
où Fp est la force appliquée sur l'engin et est le débit de matière éjectée.
Cette masse éjectée est appelée masse propulsive en opposition aux masses utile et de structure qui comprennent la masse du vaisseau ne servant pas à accélérer.
Pour qu'un moteur à réaction fonctionne, il lui faut donc deux éléments : de la masse propulsive et de l'énergie. La variation de quantité de mouvement du vaisseau lors de l'éjection d'une particule de masse m à une vitesse v sera donc égale à la quantité de mouvement transmise à la particule, soit m v. L'énergie cinétique de la particule quant à elle est de m v2 / 2 et doit être fournie par le système propulsif. Tous les systèmes de propulsion chimique utilisent la combustion comme source d'énergie. Les produits de cette combustion sont ensuite relâchés, devenant masse propulsive. Dans un système de propulsion spatiale électrique, l'électricité est utilisée pour accélérer des ions formant la masse propulsive. Ces systèmes ont donc besoin d'énergie électrique pour fonctionner. Celle-ci peut être fournie par des panneaux solaires photovoltaïques ou par des réacteurs nucléaires[11].
Lors de la conception de systèmes de propulsion spatiale, les concepteurs concentrent souvent leurs efforts sur la diminution de la masse propulsive emportée. La masse propulsive doit en effet accompagner le vaisseau tant qu'elle n'est pas utilisée et est perdue irrémédiablement une fois consommée. La réduire au maximum permet donc de minimiser la taille et la masse des réservoirs. Une manière de déterminer la quantité de mouvement que l'on peut obtenir à l'aide d'une masse propulsive donnée est l'impulsion spécifique, qui équivaut à la quantité de mouvement obtenue par unité de poids de carburant sur Terre (habituellement notée ). Elle se mesure en secondes.
L'impulsion spécifique s'écrit donc ainsi :
où F est la poussée fournie par la propulsion, le débit de matière éjectée et g0 l'accélération due au champ de gravité, supposé constant à proximité de la surface d'une planète. La dimension de Isp est ainsi un temps qui s'exprime en secondes.
Comme le poids de carburant sur Terre est souvent inutile dans une discussion d'un moteur spatial, l'impulsion spécifique peut être calculée par unité de masse. Cette formulation donne à l'impulsion spécifique la dimension d'une vitesse (i.e. m/s) [pas très clair...]. L'impulsion spécifique est dans ce cas la vitesse d'éjection efficace du moteur à réaction (habituellement notée ). Les auteurs font parfois la confusion et nomment impulsion spécifique la vitesse d'éjection efficace. Pourtant les deux diffèrent d'un terme g0, l'accélération standard de la gravité au niveau de la mer soit 9,806 65 m s−2 ().
Un moteur-fusée ayant une vitesse d'éjection importante peut par conséquent générer une variation de quantité de mouvement importante avec une masse propulsive réduite. En revanche l'énergie cinétique à fournir à une particule est proportionnelle à sa masse, mais varie comme le carré de sa vitesse d'éjection. Par conséquent un système très efficace sur le plan de la masse propulsive demande beaucoup d'énergie et est souvent moins efficace d'un point de vue de l'énergie totale dépensée. De plus, il faut garder à l'esprit que si le gain en masse propulsive se fait aux dépens de la masse globale du vaisseau, par exemple, par l'ajout d'une grande surface de panneaux solaires pour fournir de l'énergie, le bilan de masse peut au bout du compte devenir négatif. Ce problème devient critique pour un système devant fournir une forte poussée. En effet générer une grande quantité de mouvement avec peu de masse propulsive implique une très grande vitesse d'éjection donc beaucoup d'énergie à fournir. En conséquence, la plupart des moteurs très efficaces sur un plan de la masse propulsive embarquée fournissent une poussée très faible en raison de l’inexistence de systèmes embarqués pouvant générer assez d'énergie.
Delta-v et carburant[modifier | modifier le code]

À supposer qu'on utilise un vaisseau spatial en dehors de toute interaction extérieure, la consommation de son carburant au travers de son système propulsif dans une direction donnée provoquerait une modification de sa vitesse. La différence totale entre la vitesse initiale du véhicule et sa vitesse finale (i.e. après la poussée) est appelée delta-v ().
Si la vitesse d'éjection efficace du système de propulsion ne varie pas durant la poussée, le delta-v total peut être calculé en utilisant l'équation de Tsiolkovski.
où :
- v est la variation de vitesse entre le début et la fin de la phase propulsée considérée ;
- ve est la vitesse d'éjection de la masse propulsive;
- mi est la masse totale du vaisseau au début de la phase propulsée (i pour initial) ;
- mf est la masse totale du vaisseau à l'issue de la phase propulsée (f pour final), exprimée dans la même unité que mi ;
- est la fonction logarithme népérien.
Pour des raisons historiques, on remplace parfois de la manière présentée préalablement :
où l' est l'impulsion spécifique et est la constante d'accélération gravitationnelle au niveau de la mer.
Pour une mission ayant besoin de beaucoup de delta-v, la majorité de la masse du vaisseau est souvent de la masse propulsive. Comme un vaisseau doit emporter toute sa masse propulsive, une grande partie de la masse propulsive consommée l'est en réalité pour accélérer de la masse propulsive, qui sera utilisée plus tard, plutôt que de la masse utile. Si un vaisseau, dont la masse finale mf comprend la masse utile ainsi que la masse de structure, doit accélérer d'un delta-v avec un système propulsif de vitesse d'éjection , mp la masse propulsive nécessaire peut être calculée en utilisant l'équation de Tsiolkovski de la manière suivante :
Ainsi pour des bien plus petits, l'équation devient quasi linéaire et une masse propulsive très réduite est nécessaire. Si est du même ordre de grandeur que alors le besoin en masse propulsive est typiquement égal environ deux fois la masse utile et de structure du vaisseau. À partir de là, l'augmentation de masse propulsive devient exponentielle. Pour des très supérieurs à la vitesse d'éjection, un ratio de masse très important est nécessaire entre masse propulsive et masse utile.
Pour une mission nécessitant, par exemple, un décollage ou un atterrissage sur une planète, les effets de la gravité et de la traînée créée par l'atmosphère doivent être compensés par de la masse propulsive supplémentaire. Il est courant d'intégrer de tels effets dans un bilan de delta-v. Ainsi un lancement vers une orbite basse terrestre demande un delta-v entre 9,3 km/s et 10 km/s. Ces bilans de delta-v sont habituellement calculés numériquement.
Quelques effets particulier comme l'effet Oberth ne peuvent être utilisés qu'avec des systèmes propulsifs à très forte poussée comme ceux utilisés sur les lanceurs (l'accélération doit être importante).
Puissance et efficacité énergétique[modifier | modifier le code]

Pour tous les moteurs à réaction (comme les moteurs-fusées ou la propulsion ionique) une partie de l'énergie doit être transmise à la masse propulsive pour l’accélérer. Tout système propulsif va dissiper de l'énergie lors de ce processus, mais, même en supposant l'accélération parfaite, l'énergie cinétique à transmettre à la masse propulsive sera toujours donnée par la formule suivante[12]:
La comparaison entre l'équation de Tsiolkovski et celle de l'énergie cinétique montre que, même à supposer que le rendement du système propulsif soit de 100 %, toute cette énergie ne finit pas dans l'énergie cinétique du véhicule, le reste étant perdu dans la masse propulsive une fois cette dernière éjectée.
Le ratio entre énergie dissipée dans la masse propulsive et énergie communiquée au vaisseau dépend de la conception du vaisseau et de la mission. On peut souligner quelques règles importantes en la matière :
- si l'on fixe l', pour un delta-v donné, il existe une qui minimise l'énergie totale nécessaire au vaisseau pour accélérer. Cette impulsion spécifique correspond à une vitesse d'éjection d'environ deux tiers du delta-v. Les moteurs ayant par conséquent des impulsions spécifiques très élevées sont loin de l'idéal énergétique pour une mission à faible delta-v.
- si l'impulsion spécifique peut être variable à tout instant du vol de manière à être en permanence égale et opposée à la vitesse du vaisseau, alors le minimum absolu d'énergie nécessaire pour propulser le vaisseau est atteint. Cela signifie qu'à son éjection la masse propulsive est immobile dans l'espace[Note 1] et n'a plus d'énergie cinétique. En principe un tel système aurait une efficacité de 100 %, mais en pratique il y aura des pertes thermiques et une température résiduelle dans la masse propulsive. Dans la plupart des cas, cette solution demande une quantité de carburant impossible à fournir avec les moyens actuels. Par ailleurs le vaisseau a également besoin dans ce cas d'une vitesse initiale.
Certains systèmes propulsifs encore en phase d'essai comme le VASIMR ou les propulseurs à force pondéromotrice peuvent modifier de manière importante leur vitesse d'éjection. La variation de l'impulsion spécifique permet de modifier l'utilisation de la masse propulsive et d'améliorer l'accélération à différentes phases du vol. Cependant les meilleures performances demandent à nouveau une vitesse d'éjection proche de la vitesse du véhicule. La plupart de ces concepts de moteurs ioniques et plasmiques ont une vitesse d'éjection bien supérieure à la vitesse du véhicule. À titre d'exemple, le VASIMR a une vitesse d'éjection minimale autour de 15 km/s alors que, en comparaison, le delta-v orbite terrestre - orbite lunaire est de 4 km/s.
Il est souvent proposé dans les missions utilisant ce genre de technologie d'utiliser des générateurs électriques très puissants basés, par exemple, sur l'énergie nucléaire. Si cette solution peut être intéressante, la croissance très rapide de la masse du système électrique peut rendre le concept impraticable. En effet, comme expliqué préalablement, la croissance de la puissance du système électrique est souvent linéairement liée à la croissance de sa masse alors que l'énergie est liée au carré de la vitesse.
Énergie[modifier | modifier le code]
La structure abstraite suivante peut s'appliquer de façon générale aux différents types de moteurs à réaction :

Dans le cas idéal où est la masse utile du vaisseau et où est sa masse propulsive (on suppose ainsi que la masse de structure est nulle). L'énergie nécessaire pour accélérer la masse propulsive d'une vitesse est :
Ceci correspond à une énergie cinétique nulle pour la masse propulsive une fois celle-ci relâchée. On se place donc ici dans le cas où la vitesse d'éjection est égale à la vitesse du vaisseau. Si l'on suppose à présent le vaisseau fixe, la masse propulsive est alors accélérée d'une vitesse nulle jusqu'à la vitesse d'éjection et toute l'énergie est transmise à la masse propulsive. Dans la plupart des cas néanmoins on se trouve entre ces deux cas limites et le vaisseau perd une partie de l'énergie cinétique créée en raison de la vitesse d'éjection de la masse propulsive. Prenons l'exemple où l'on a une vitesse d'éjection = 10 km/s et une vitesse du vaisseau de 3 km/s. Durant le fonctionnement du système propulsif, on a donc une partie de la masse propulsive dont la vitesse est modifiée et passe de 3 km/s dans le sens d'avancée du vaisseau à 7 km/s dans le sens opposé de la vitesse du vaisseau. Par conséquent, sur les 50 MJ/kg dépensés pour accélérer la masse propulsive, 24,5 MJ/kg sont perdus dans l'accélération de la masse propulsive (de 0 à 7 km/s) et par conséquent seulement 25,5 MJ/kg sont utilisés pour l'accélération du vaisseau.
Dans le cas général, cette équation s'écrit ainsi :
où est la vitesse du véhicule, la vitesse d'éjection de la masse propulsive et la masse du véhicule.
Par conséquent la densité massique d'énergie gagnée par le véhicule spatial durant un intervalle de temps est l'énergie gagnée par le véhicule, incluant la masse propulsive non consommée, divisée par la masse du véhicule. Cette énergie gagnée par le véhicule est égale à l'énergie produite par le système de propulsion moins l'énergie perdue dans la masse propulsive éjectée. Plus la vitesse du véhicule est élevée, moins la perte énergétique dans la masse propulsive éjectée est importante ; si le véhicule se déplace à plus de la moitié de la vitesse d'éjection alors la masse éjectée perd même de l'énergie au profit du véhicule.
On a :
où est la densité massique d'énergie mécanique du véhicule. Dans le cas où l'on utilise le système propulsif pour décélérer en éjectant donc la masse dans la direction de la vitesse, devient négatif.
Cette formule s'applique à nouveau uniquement pour le cas idéal où le vaisseau n'a aucune perte énergétique, par exemple, par chaleur. Les pertes étant de toute manière au désavantage du système propulsif, que cela soit en accélération ou en décélération, puisqu'elles réduisent l'énergie dédiée à la poussée.
Si l'énergie est produite par la masse propulsive elle-même, comme dans un moteur chimique, la densité énergétique doit être , sachant que les masses du réducteur et de l'oxydant doivent être prises en compte. Un exemple courant est = 4,5 km/s, correspondant à une densité énergétique de 10,1 MJ/kg (combustion de l'hydrogène). La densité énergétique réelle de cette combustion est plus importante, mais les pertes thermiques et mécaniques entraînent cette valeur plus réduite.
L'énergie nécessaire peut ainsi s'écrire :
En conclusion
- Pour on a
- Pour un donné, l'énergie minimum est atteinte si , ce qui demande une énergie :
- .
- Partant d'une vitesse nulle, ceci représente 54,4 % d'énergie en plus que la simple énergie cinétique de la masse finale du véhicule en fin de poussée.
Tous ces résultats ne sont valables que pour une vitesse d'éjection fixe.
En raison de l'effet Oberth, et en supposant que la poussée débute à une vitesse non nulle, l'énergie que doit développer le système propulsif peut être inférieure à la différente d'énergie cinétique de la masse finale du véhicule (c'est-à-dire la somme de la masse de structure, de la masse utile et de la masse propulsive non consommée). C'est le cas, par exemple, lorsque la masse propulsive est éjectée à une vitesse inférieure que celle du véhicule ; dans ce cas le véhicule peut s'approprier une partie ou l'intégralité de l'énergie cinétique initiale de la masse propulsive (due à sa vitesse avant la poussée).
La puissance est donnée par :
où est la poussée et est l'accélération du véhicule. Par conséquent la poussée disponible théorique par unité de puissance est de deux divisé par la vitesse d'éjection. L'efficacité de la poussée est calculée en comparant la poussée réelle du moteur avec cette poussée théorique.
Dans le cas de faible puissance disponible (en utilisant un panneau solaire, par exemple), l'accélération est réduite, en effet dans le cas d'une grande vitesse d'éjection des moteurs électriques on a donc une accélération possible très faible, cela augmente donc le temps nécessaire pour obtenir le . La vitesse d'obtention du est par conséquent inversement proportionnelle à la vitesse d'éjection pour une efficacité de 100 %.
Pour on a donc , avec le temps de poussée.
Exemples
- Pour une puissance de 1 000 W, un véhicule d'une masse de 100 kg, un moteur avec = 16 km/s demande 1,5 mois de poussée pour = 5 km/s.
- Pour une puissance de 1 000 W, un véhicule d'une masse de 100 kg, un moteur avec = 50 km/s demande 5 mois de poussée pour = 5 km/s.
Rapport puissance poussée[modifier | modifier le code]
Le rapport puissance sur poussée s'écrit[12] :
Par conséquent pour un véhicule de puissance P, la poussée s'écrit :
Exemple pour plusieurs moteurs à réaction[modifier | modifier le code]
Supposons que l'on souhaite envoyer une sonde de 10 000 kg vers Mars. Le delta-v nécessaire à partir de l'orbite basse terrestre est environ de 3 000 m/s en utilisant un transfert d'Hohmann. Dans cet exemple, on supposera que les systèmes de propulsion proposés ci-après sont tous compatibles avec une telle manœuvre.
| Moteur | Vitesse d'éjection efficace (km/s) |
Impulsion spécifique (s) |
Masse propulsive (kg) |
Énergie nécessaire (GJ) |
Densité massique d'énergie de la masse propulsive |
Ratio puissance/poussée minimal | Ratio Masse/Poussée du générateur de puissance* |
|---|---|---|---|---|---|---|---|
| Propulsion à propergol solide | 1 | 100 | 190 000 | 95 | 500 kJ | 0,5 kW/N | N/A |
| Propulsion à ergols liquides | 5 | 500 | 8 200 | 103 | 12,6 MJ | 2,5 kW/N | N/A |
| Moteur ionique | 50 | 5 000 | 620 | 775 | 1,25 GJ | 25 kW/N | 25 kg/N |
| Système de propulsion avancée (concept) | 1 000 | 100 000 | 30 | 15 000 | 500 GJ | 500 kW/N | 500 kg/N |
* - suppose une puissance massique de 1 kW/kg
On peut observer ici que les moteurs consommant peu de carburant peuvent effectivement diminuer de beaucoup la masse propulsive en comparaison de la masse utile : ici la sonde de 10 t. La masse peut parvenir à des proportions négligeable comme dans le cas du concept de propulsion avancée. En revanche il faut noter que dans ce cas l'énergie nécessaire est très importante. À cela s'ajoute le problème du rapport poussée/poids d'un véhicule devant être supérieur à 1 si l'on décolle d'un astre. Pour arriver à de tels niveaux de poussée, les systèmes de propulsion électrique doivent développer des puissances de l'ordre du Gigawatt ce qui est l'équivalent de la consommation électrique d'une petite ville industrialisée. C'est donc actuellement impossible à la vue des techniques de génération de puissance que l'on peut embarquer dans un véhicule spatial.
Certains concepts alternatifs utilisent une transmission de la puissance d'un générateur non embarqué, en focalisant par exemple l'énergie d'un laser ou d'un autre faisceau énergétique sur le véhicule, la masse propulsive ne servant alors plus à donner l'énergie servant à la propulsion mais étant simplement là pour être accélérée par cette énergie extérieure. Ce genre de concepts présente néanmoins de grandes difficultés dans sa mise en œuvre tant dans l'espace qu'au sol.
La génération d'énergie à faible puissance et son accumulation pour être relâchée par décharges successives dans le propulseur est également utilisée. Ces solutions sont utilisables uniquement une fois déjà dans l'espace. Après une longue phase de propulsion par petits jets successifs la sonde atteint alors le delta-v recherché. Par exemple la sonde SMART-1 utilisant un moteur ionique a eu plusieurs centaines de phases propulsives générant petit à petit le delta-v nécessaire pour l'envoyer en orbite autour de la Lune. Cette méthode a demandé plus d'un an d'attente avant d'arriver sur la Lune alors que des méthodes de propulsion chimique demandent moins d'une semaine. En revanche la quantité de carburant nécessaire a été bien plus faible que pour un moteur chimique et la masse au lancement est souvent un facteur de coût important dans les missions spatiales.
Par conséquent la sélection préliminaire de toute mission doit prendre en compte ces différents facteurs (masse, temps d'opération, flexibilité une fois sur orbite, fenêtres de tirs, etc.) afin de déterminer quel concept est le moins coûteux et offrira les meilleures chances de succès.
Moteurs-fusées[modifier | modifier le code]

La plupart des moteurs-fusées sont des moteurs à combustion interne, même si certains types de moteurs n'utilisant pas de combustion existent. Les moteurs-fusées produisent en général une masse propulsive de haute température, éjectée sous la forme d'un gaz très chaud. Cette température est produite par combustion d'un carburant solide, liquide ou gazeux en présence d'un oxydant dans une chambre de combustion. Ces gaz extrêmement chauds sont alors conduits vers une tuyère pour être détendus. Ces tuyères, habituellement en forme de cloche donnent à la plupart des moteurs-fusées leur aspect si reconnaissable. Ces tuyères permettent la détente et l'accélération du gaz d'échappement, transférant ainsi l'énergie thermique du gaz en énergie cinétique. Les vitesses d'éjection de tels moteurs sont habituellement comprises entre 2 et 10 fois la vitesse du son au niveau de la mer.
Dans le domaine de la propulsion spatiale, les moteurs-fusées produisent les puissances et les poussées spécifiques les plus importantes.
Certains concepts de moteurs-fusées utilisant la propulsion nucléaire thermique permettent également d'atteindre des puissances et poussées proches des niveaux des moteurs-fusées chimiques, mais leur utilisation se limite à des démonstrateurs d'essai.
Propulsion électrique[modifier | modifier le code]

Ne s'appuyant pas sur la détente de gaz à haute température pour accélérer la masse propulsive, ces moteurs utilisent un large choix de solutions pour l'accélérer en utilisant des forces électrostatiques ou électromagnétiques. Dans ce genre de système, la masse propulsive est habituellement un flux d'ions. Ces moteurs utilisent l'énergie électrique pour ioniser les atomes de la masse propulsive puis créent des champs électriques pour accélérer les ions jusqu'à leur vitesse d'éjection.
Le concept de propulsion électrique date de 1906 lorsque Robert Goddard la proposa dans son carnet de recherche[13]. Constantin Tsiolkovski publia le concept en 1911.
Pour ces systèmes de propulsion, qui produisent de grandes vitesses d'éjection, l'efficacité énergétique et la poussée sont inversement proportionnelles à leur vitesse d'éjection. Leurs grandes vitesses d'éjection demandant de grandes puissances électriques et rendant ces concepts impossibles pour de fortes poussées par manque de systèmes de production d'énergie suffisamment puissants. Ces systèmes peuvent en théorie utiliser presque n'importe quelle sorte de masse propulsive.
Pour certaines missions, en particulier celles proches du Soleil, l'énergie solaire est suffisante et a souvent été utilisée par le passé, mais pour explorer des astres plus lointains hors du Système solaire interne, telles que Jupiter ou Saturne, d'autres moyens de production de l'électricité doivent être trouvés, comme l'énergie nucléaire. Ces concepts sont appelés propulsion nucléaire électrique.
Dans la plupart de ces concepts, la masse du système de production et de conversion de l'énergie est bien plus importante dans la conception du vaisseau que la masse propulsive car très sensible aux besoins de la mission.
La plupart des réacteurs nucléaires offre des puissances spécifiques environ de moitié inférieures aux puissances développées par les panneaux solaires à proximité de la Terre. Des générateurs chimiques d'électricité ne sont pas envisagés pour ces concepts car trop limités en énergie totale. Les concepts utilisant de l'énergie dirigée (laser, particules, etc.) envoyées vers le vaisseau depuis la Terre peuvent potentiellement être une solution mais sont aujourd'hui à l'état de concept non démontré technologiquement. À cela s'ajoute que tous ces systèmes de propulsion ont des rendements de conversion énergétiques trop faibles pour atteindre des vitesses permettant des voyages interstellaires.

Quelques méthodes de propulsion électrique :
- Moteurs ioniques (accélère d'abord les ions puis neutralise le flux émit grâce à une électrode neutralisante.)
- Propulseurs électrothermiques (des champs électromagnétiques sont utilisés pour créer un plasma pour augmenter la température de la masse propulsive, l'énergie thermique ainsi communiquée est ensuite convertie en énergie cinétique au travers d'une tuyère physique ou magnétique).
- Propulseurs electromagnétiques (les ions sont accélérés soit par Force de Lorentz, soit par l'effet de champs électromagnétiques là où le champ électrique n'est pas colinéaire à l'accélération).
Dans les propulseurs électrothermiques et électromagnétiques, les ions et les électrons sont accélérés en même temps, une neutralisation du faisceau n'est par conséquent pas nécessaire.
Propulseurs sans masse propulsive embarquée[modifier | modifier le code]
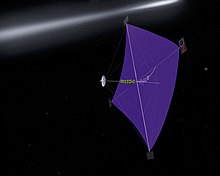
La loi de la conservation du moment déclare qu'un propulseur n'utilisant aucune masse propulsive ne peut accélérer le centre de masse du vaisseau (changer son orientation en revanche est possible). Cependant l'espace n'est pas totalement vide, en particulier lorsqu'on reste dans les limites du Système solaire. Il existe des champs de gravité, des champs magnétiques, des vents solaires et d'autres radiations, solaires, par exemple. De nombreux concepts de propulsion tentent de profiter de ces environnements pour accélérer le vaisseau. Cependant comme ces effets sont très diffus, les structures propulsives mises en jeu sont souvent très importantes pour pouvoir en profiter.
Il existe plusieurs concepts de propulsion utilisant aucune ou peu de masse propulsive pour fonctionner. Le concept du satellite captif, par exemple, emploie un long câble très résistant pour changer d'orbite reproduisant à plus petite échelle le concept de l'effet de fronde[14]. Les voiles solaires utilisent la pression de radiation solaire pour se propulser, ce qui demande une grande surface d'exposition aux radiations solaires et de grands efforts pour limiter la masse du vaisseau. Les voiles magnétiques dévient les particules chargées des vents solaires grâce à un champ magnétique, récupérant ainsi une partie de leur quantité de mouvement. Une variante de ce concept est appelée propulsion plasmique mini-magnétosphérique et qui utilise un petit nuage de plasma pour modifier la trajectoire de ces mêmes particules. Les concepts de voiles électriques quant à eux proposent l'utilisation de fils très fins et très légers au travers desquels un courant électrique permanent permet la déviation des particules des vents solaires. Quelques démonstrations en vol ont été faites de concept de voile solaire comme IKAROS ou NanoSail-D2[15].
Un vaisseau spatial est soumis au théorème de la conservation du moment cinétique ; par conséquent tout changement de son moment est le produit d'une force désaxée (principe du Reaction Control System), donc d'une masse propulsive éjectée, ou de la création d'un moment inverse dans le vaisseau (principe des roues de réaction). Les forces extérieures non conservatives, comme la gravité ou la traînée atmosphérique, peuvent contribuer à la création de moment dans le vaisseau spatial[16]. Un système de contrôle de l'attitude est donc nécessaire dans les vaisseaux spatiaux pour pouvoir gérer l'orientation[17].
Une autre méthode est l'assistance gravitationnelle[18] qui peut accélérer une sonde sans masse propulsive en récupérant une partie de l'énergie cinétique d'une planète par gravité. Ces assistances gravitationnelles peuvent permettre des niveaux d'accélération très important si elles sont combinées à l'utilisation d'un moteur-fusée.
Propulsion planétaire et atmosphérique[modifier | modifier le code]
Pour le lancement depuis la Terre, la poussée est un facteur très important. En effet, la gravité tend à retenir le lanceur tandis qu'il s'élève vers l'espace et par conséquent la poussée du système de propulsion doit impérativement être supérieure à la pesanteur. Beaucoup de types de propulsion présentés dans la section précédente, telle que la propulsion ionique, ne permettent pas d'obtenir un rapport poussée sur poids supérieur à 1 et ne peuvent par conséquent pas être utilisés pour un lancement depuis la Terre.
La plupart des vaisseaux spatiaux utilisent des moteurs-fusées chimiques pour le lancement depuis la Terre. D'autres sources de puissance comme la propulsion nucléo-thermique ont été proposées et testée, mais, pour des raisons politiques, environnementales et de sûreté, n'ont jusqu'à présent jamais été utilisées.
Systèmes de lancement assistés[modifier | modifier le code]

L'un des avantages des vaisseaux spatiaux partant du sol est qu'ils pourraient disposer a priori de l'aide d'infrastructures terrestres. Les propositions de lancement spatial sans fusée comprennent beaucoup de projets dont la taille limite leur application dans un proche futur. On pourra citer par exemple :
- les ascenseurs spatiaux
- les « boucles » de lancement (launch loop - un système de 2 000 km tractant le vaisseau vers une orbite basse)
- les fontaines spatiales (space fountain - un système de structure remontant vers l'espace maintenu par un jet de particules)
- les anneaux orbitaux (orbital ring - un système d'anneau en orbite dérivé de l'ascenseur spatial et permettant d'accélérer les vaisseaux vers des orbites supérieures)
- les catapultes électromagnétiques (Canon électrique, Canon magnétique)
- le lancement sur traîneau (le premier étage du vaisseau est un traîneau propulsé le long d'une pente et récupérable)
- les canons spatiaux
- les plateformes à haute altitude
- les ballons spatiaux (orbital airship - dirigeable permettant d'atteindre une très haute altitude pouvant alors être accélérés par un système de propulsion à faible poussée allant jusqu'à la vitesse orbitale).
Moteurs aérobies[modifier | modifier le code]

La plupart des études montrent que la majorité des moteurs aérobies conventionnels comme les turboréacteurs ou statoréacteurs ont un rapport poussée/poids trop faible pour être utilisés sur des vaisseaux spatiaux sans sacrifier de la performance. En revanche le lanceur pourrait être lancé depuis un véhicule utilisant ce mode de propulsion (comme pour Pegasus ou SpaceShipTwo). Certains concepts de systèmes cités dans les systèmes de lancement assistés comme les lancements sur traîneau utilisent également des moteurs aérobies.
En parallèle, certains moteurs particuliers sont étudiés actuellement pour leur utilisation sur des vaisseaux spatiaux durant la montée initiale (la phase de vol atmosphérique) :
- SABRE - un turboréacteur à hydrogène utilisant un refroidisseur[19] ;
- ATREX - un autre turboréacteur à hydrogène utilisant un refroidisseur[20]
- Moteur à cycle à air liquéfié (en) - un moteur liquéfiant l'air avant de l'utiliser comme comburant dans un moteur-fusée ;
- Superstatoréacteur - un moteur à réaction utilisant une combustion supersonique.
La plupart des lanceurs décollent à la verticale puis progressivement inclinent leur trajectoire pour l'amener à l'horizontale en exploitant les forces de gravité (gravity turn). Cette manœuvre est réalisée à une altitude de plusieurs dizaines de kilomètres. La première phase de montée à la verticale permet de limiter l'énergie perdue par frottement atmosphérique en réduisant le temps passé à basse altitude, là où l'atmosphère est la plus dense et donc où les forces de frottement sont plus importantes. Les moteurs aérobies sont bien plus efficaces que les moteurs fusées durant cette phase et par conséquent dans les concepts de fusée utilisant un étage aérobie, le lanceur passe une partie plus importante de sa phase propulsée dans l'atmosphère de manière à utiliser au mieux ces moteurs.
Rentrée atmosphérique, capture planétaire et atterrissages non propulsés[modifier | modifier le code]

Lorsqu'un vaisseau spatial entre dans la sphère d'influence d'une planète pour se placer en orbite, ou lorsqu'un vaisseau souhaite atterrir sur cette planète, il doit ajuster sa vitesse. Cette manœuvre peut être réalisée par certaines méthodes utilisant l'atmosphère de l'astre permettent de réduire le coût en carburant de ces manœuvres (si elles apportent suffisamment de delta-v).
- La rentrée atmosphérique utilise un bouclier thermique pour réduire la vitesse du vaisseau grâce à la traînée aérodynamique et lui permettre ainsi d'approcher le sol à des vitesses permettant l'utilisation d'autres moyens de freinage.
- L'aérofreinage permet à un vaisseau d'abaisser son apoapse (la plus haute altitude de l'orbite) en utilisant la traînée induite par les hautes couches de l’atmosphère de la planète pour ralentir lors de son passage au périapse (la plus basse altitude de l'orbite). Cette méthode permet de réduire considérablement la consommation de carburant nécessaire à la manœuvre de circularisation de l'orbite car elle demande bien moins de carburant qu'une manœuvre purement propulsive. Étant donné que ce freinage est réalisé au cours d'un grand nombre d'orbites, l'aérofreinage ne provoque pas un échauffement important et un bouclier thermique n'est pas nécessaire. Cette méthode a été utilisée pour plusieurs missions martiennes comme Mars Reconnaissance Orbiter, Mars Odyssey, Mars Global Surveyor et au moins sur une mission vers Vénus, Magellan.
- L'aérocapture est une manœuvre bien plus brutale consistant à convertir une orbite hyperbolique (le vaisseau n'est pas encore capturé par la planète) en une orbite elliptique en un seul passage au travers de l'atmosphère. La traînée nécessaire étant bien plus importante que pour l'aérofreinage, un bouclier thermique et un système de guidage et de navigation très robustes sont nécessaires. Un des principaux problèmes est que l'atmosphère d'une planète est un milieu en constante évolution en raison d'un grand nombre de paramètres comme les cycles solaires ou les cycles climatiques, une modélisation fine des atmosphères est très complexe et comme aucun passage de test préalable à la manœuvre n'est possible au contraire de l'aérofreinage, le système doit être robuste aux évolutions de l'atmosphère. Si l'intention est de se placer en orbite de la planète, une manœuvre propulsive de remontée du périgée est nécessaire après le passage dans l'atmosphère pour éviter que le vaisseau n'y plonge une seconde fois. L'aérocapture n'est pour le moment qu'au stade de concept et n'a jamais été testé lors d'une mission interplanétaire. Pour autant, le concept a été en partie testé avec Zond 6, Zond 7 et Zond 8 qui ont fait à leur retour de la Lune une manœuvre de rentrée atmosphérique en deux temps transformant d'abord leur trajectoire hyperbolique en une trajectoire elliptique de rentrée, démontrant la première phase de l'aérocapture et n'ayant pas rehaussé leur périgée par la suite, replongeant donc dans l'atmosphère.
- Le ballute est un système gonflable permettant l'augmentation de la traînée pour des atterrissages ou des freinages atmosphériques.
- Les parachutes sont utilisés classiquement pour l’atterrissage de sondes sur des planètes pourvues d'une atmosphère généralement après qu'un bouclier thermique ait supprimé la majeure partie de la vitesse de rentrée.
- Le Lithobreaking (en français, « freinage par le sol ») est une catégorie plus générale utilisant le sol pour assurer le freinage final. Un bon exemple est l'utilisation possible de coussins gonflables (« airbags ») pour amortir l’atterrissage comme pour la mission Mars Pathfinder. Certaines missions ont pour but d'impacter l'astre visé soit sans résister à l'impact comme pour la mission LCROSS, soit en résistant à l'impact comme pour la mission Deep Space 2 et par conséquent le véhicule percute le sol avec une vitesse encore élevée. D'autres manœuvres consistent à effectuer un posés doux sur l'astre visé avec un minimum de vitesse pour que la sonde résiste à l'impact la plupart du temps en rajout à la mission initiale comme pour la mission NEAR Shoemaker.
Concepts futuristes[modifier | modifier le code]
Beaucoup de concepts futuristes sont proposés dans le domaine de la propulsion spatiale. La plupart sont à prendre avec beaucoup de précaution quant à leur faisabilité tant leurs hypothèses sont difficiles à démontrer. Des exemples de tels concepts hautement spéculatifs sont représentés au sein du programme de physique avancée des propulseurs de la NASA. On y retrouve :
- la propulsion diamétrique,
- la propulsion disjonctive,
- la propulsion intense,
- la propulsion biaise,
- la propulsion d'Alcubierre,
- la voile différentielle.
Classification des différents types de propulsion[modifier | modifier le code]
Types de propulsion[modifier | modifier le code]
Propulsion classique[modifier | modifier le code]
Propulsion avancée[modifier | modifier le code]
- Propulsion spatiale hybride
- Propulsion nucléaire
- Propulsion électrique :
- Propulsion électromagnétique : propulseur magnétoplasmadynamique
- Propulsion électrostatique : Propulseur ionique à bombardement, Propulseur à effet Hall (SPT),
- Propulsion électrothermique : VASIMR
- Propulsion héliothermique
- Propulsion aérobie
- Propulsion laser
- Voile :
Propulsion exotique[modifier | modifier le code]
- EmDrive
- Magnétohydrodynamique
- Antimatière
- Moteur d'Alcubierre
- Ascenseur spatial
- Propulsion captive
- Propulsion photonique
- Programme de physique avancée des propulseurs
Tableau comparatif[modifier | modifier le code]
Ci-après se trouve un tableau récapitulant les méthodes de propulsion spatiale allant des plus classiques à des concepts plus futuristes. Les caractéristiques suivantes sont données :
- la vitesse d'éjection efficace, en km/s soit l'efficacité du moteur à fournir un mouvement à partir d'une quantité donnée de masse propulsive ;
- la poussée, en N soit la capacité du système à fournir une force propulsive et donc la vitesse à laquelle il accélère le vaisseau ;
- la durée de propulsion, l'ordre de grandeur du temps de propulsion que ce système peut assurer ;
- le delta-v maximum possible avec un tel système, soit l'accélération totale du vaisseau que le système peut assurer entre le début et la fin de sa mission ;
- le Technology Readiness Level (en français, « Niveau de Maturité Technologique »), une échelle de 1 à 9 permettant d'évaluer si le système est réalisable facilement, 1 étant un système immature technologiquement et 9 étant un système démontré technologiquement.
| Méthodes | Vitesse d'éjection spécifique (km/s) |
Poussée (N) |
Temps de poussée (ordre de grandeur) |
Delta-v maximum (km/s) |
Niveau de maturité technologique |
|---|---|---|---|---|---|
| Propulsion à propergol solide | 1 – 4 | 103 - 107 | minutes | ~ 7 | 9:Démontré en vol |
| Propulsion hybride | 1,5 – 4,2 | <0,1 - 107 | minutes | > 3 | 9:Démontré en vol |
| Propulsion liquide Monergol | 1 – 3 | 0,1 - 100 | millisecondes-minutes | ~ 3 | 9:Démontré en vol |
| Propulsion liquide biergols | 1 – 4,7 | <0,1 - 107 | minutes | ~ 9 | 9:Démontré en vol |
| Propulseur ionique électrostatique | 15 – 210[21] | 10-3 - 10 | mois/années | > 100 | 9:Démontré en vol |
| Propulseur à effet Hall | 8 – 50 | 10-3 - 10 | mois/années | > 100 | 9:Démontré en vol |
| Résistojet | 2 – 6 | 10-2 - 10 | minutes | ? | 8:Qualifié pour le vol[22] |
| Arcjet | 4 – 16 | 10-2 - 10 | minutes | ? | 8:Qualifié pour le vol |
| Field Emission Electric Propulsion | 100 – 130[23] | 10-6 - 10-3[23] | mois/années | ? | 8:Qualifié pour le vol[23] |
| Propulseur plasmique pulsé | ~ 20 | ~ 0,1 | ~2,000–10,000 heures | ? | 7:Démonstrateur testé en vol |
| Propulsion liquide double mode | 1 – 4,7 | 0,1-107 | millisecondes - minutes | ? | 7:Démonstrateur testé en vol |
| Voile solaire | 299790 : Lumière 145-750 : Vent solaire |
9/km2 à 1 UA | Infini | ~ 3 – 9 | 9:Contrôle de vol par pression solaire démontré en vol (Mariner 10) 6:Déploiement démontré en vol 5:Concept validé lors de test au sol |
| Propulsion à propergol liquide triergol | 2,5 – 5,3 | 0,1 - 107 | minutes | ~ 9 | 6:Prototype démontré au sol[24] |
| Propulseur magnétoplasmadynamique | 20 – 100 | 100 | semaines | ? | 6:Prototype de 1 kW démontré en vol[25] |
| Propulsion nucléaire thermique | 9[26] | 107[26] | minutes[26] | >~ 20 | 6:Prototype démontré au sol |
| Catapulte électromagnétique | 0.001 - ~30 | 104 - 108 | mois | ? | 6:Modèle de 32 MJ démontré au sol |
| Satellite captif | N/A | 1 - 1012 | minutes | ~ 7 | 6:Modèle de 31,7 km démontré dans l'espace[27] |
| Air-augmented rocket | 5 – 6 | 0,1 - 107 | secondes-minutes | > 7 ? | 6:Prototype testé au sol[28],[29] |
| Moteur à cycle d'air liquide | 4,5 | 103 - 107 | secondes-minutes | ? | 6:Prototype testé au sol |
| Pulsed inductive thruster | 10 - 80[30] | 20 | mois | ? | 5:Composants testés sous vide[30] |
| VASIMR | 10 - 300 | 40 - 1200 | jours/mois | >100 | 5:Composants testés sous vide |
| Magnetic field oscillating amplified thruster | 10 - 130 | 0,1 - 1 | jours/mois | >100 | 5:Composants testés sous vide |
| Fusée solaire thermique | 7 - 12 | 1 - 100 | semaines | >~ 20 | 4:Composants testés en laboratoire[31] |
| Propulsion radioisotopique | 7 – 8 | 1,3 - 1,5 | mois | ? | 4:Composant testés en laboratoire |
| Propulsion nucléaire électrique (dépend de la méthode de propulsion électrique utilisée) |
Variable | Variable | Variable | ? | 4:Composants testés en laboratoire |
| Projet Orion | 20 – 100 | 109 - 1012 | plusieurs jours | ~ 30 - 60 | 3:Démonstrateur de concept de 900 kg testé[32] |
| Ascenseur spatial | N/A | N/A | infini | > 12 | 3: Concept validé |
| SABRE | 4,5 - 30 | 0,1 - 107 | minutes | 9,4 | 3: Concept validé |
| Voile magnétique | 145 - 170 | ~ 1 | infini | ? | 3: Concept validé |
| Propulsion laser | Variable | Variable | Variable | ? | 3: Démonstrateur de 71 m testé |
| Anneaux spatiaux | N/A | ~ 104 | minutes | >>11 - 30 | 2: Concept proposé |
| Propulsion nucléaire pulsée | 20 - 1000 | 109 - 1012 | années | ~ 15 000 | 2: Concept proposé |
| Propulsion nucléaire par cœur gazeux | 10 - 20 | 103 - 106 | ? | ? | 2: Concept proposé |
| Propulsion nucléaire par éléments dissous Nuclear salt-water rocket |
100 | 103 - 107 | demi-heure | ? | 2: Concept proposé |
| Propulsion par fragments de fission | 15 000 | ? | ? | ? | 2: Concept proposé |
| Fusée Nucléaire photonique | 299 790 | 10-5 - 1 | années/décennies | ? | 2: Concept proposé |
| Propulsion par fusion nucléaire | 100 - 1000 | ? | ? | ? | 2: Concept proposé |
| Propulsion nucléaire pulsée catalysée par antimatière | 200 - 4000 | ? | jours/semaines | ? | 2: Concept proposé |
| Propulsion par Antimatière | 10 000 - 100 000 | ? | jours/semaines | ? | 2: Concept proposé |
| Collecteur Bussard | 2,2 - 20 000 | ? | infini | ~ 30 000 | 2: Concept proposé |
| Méthodes | Vitesse d'éjection spécifique (km/s) |
Poussée (N) |
Temps de poussée (ordre de grandeur) |
Delta-v maximum (km/s) |
Niveau de maturité technologique |
Test des systèmes de propulsion[modifier | modifier le code]
La plupart des systèmes de propulsion spatiale sont testés au sol en reproduisant avec plus ou moins de réalisme les conditions de fonctionnement prévu. De nombreux types de test existent. Les essais sur banc d'essais de moteur-fusée sont utilisés pour la démonstration du bon fonctionnement des moteurs autant que pour leur réglage avant le vol. En raison de leur dangerosité, ces installations sont pour la plupart situées à grande distance des habitations. Les moteurs-fusées qui doivent fonctionner dans le vide, comme les propulseurs ioniques ou les moteurs d'étages supérieurs, sont testés dans des chambres de vide.
Notes et références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Spacecraft propulsion » (voir la liste des auteurs).
Notes[modifier | modifier le code]
- Comme tout est en mouvement en orbite, la question que l'on peut raisonnablement se poser est de savoir immobile par rapport à quoi ? La réponse est que pour que l'énergie soit nulle (et en absence de gravité ce qui complique la situation), la masse éjectée doit avoir une vitesse nulle par rapport à la référence initiale du vaisseau (le vaisseau avant la poussée). Il est possible d'effectuer ces calculs en utilisant d'autres référentiels mais les calculs d'énergie cinétique perdue dans la masse éjectée deviennent alors complexes dans la plupart des cas. En mécanique classique la position initiale du véhicule est le centre de masse de l'ensemble masse propulsive, structure et masse utile et est également le référentiel dans lequel cet ensemble à l'énergie mécanique la plus faible.
Références[modifier | modifier le code]
- (en) Martin Hess, « Thrusters Precisely Guide EO-1 Satellite », Space First, NASA, (lire en ligne [archive du ])
- (en) Tony Phillips, « Solar S'Mores », NASA, (consulté le )
- (en) Carrie Olsen, « Hohmann Transfer & Plane Changes »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), NASA, (consulté le )
- idariane, « MEV-1 ou le début de la maintenance des satellites en orbite ? », sur Rêves d'Espace, (consulté le )
- (en) Staff, « Hohmann Transfer & Plane Changes »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), NASA, (consulté le )
- (en) Dave Doody, « Chapter 4. Interplanetary Trajectories », Basics of Space Flight, NASA JPL, (lire en ligne)
- (en)S. Hoffman « A comparison of aerobraking and aerocapture vehicles for interplanetary missions » (August 20–22, 1984) (lire en ligne, consulté le )
— « (ibid.) », dans AIAA and AAS, Astrodynamics Conference, Seattle, Washington, American Institute of Aeronautics and Astronautics, p. 25 p. - (en) Anonymous, « Basic Facts on Cosmos 1 and Solar Sailing », The Planetary Society (consulté le )
- (en) Chuck Rahls, « Interstellar Spaceflight: Is It Possible? », Phys.org, (consulté le ).
- (en) Edward A. Zobel, « Summary of Introductory Momentum Equations », Zona Land (consulté le )
- (en) Tom Benson, « Guided Tours: Beginner's Guide to Rockets », NASA (consulté le ).
- (en) George Paul Sutton et Oscar Biblarz, Rocket Propulsion Elements : 8th Edition, Hoboken, N.J., Wiley, , 768 p. (ISBN 978-0-470-08024-5, lire en ligne).
- (en) « A Critical History of Electric Propulsion: The First 50 Years (1906–1956) », Journal of Propulsion and Power, vol. 20, no 2, , p. 193–203 (DOI 10.2514/1.9245, lire en ligne)
- (en) Dave Drachlis, « NASA calls on industry, academia for in-space propulsion innovations », sur NASA, (consulté le )
- (en) Jonathan Amos, « Tiny cube will tackle space junk », BBC News, (lire en ligne)
- (en) Desmond King-Hele, Satellite orbits in an atmosphere : Theory and application, Springer, , 291 p. (ISBN 978-0-216-92252-5, lire en ligne).
- (en) « Satellite attitude control and power tracking with energy/momentum wheels », Journal of Guidance, Control, and Dynamics, vol. 43, no 1, , p. 23–34 (DOI 10.2514/2.4705).
- (en)http://www2.jpl.nasa.gov/basics/bsf4-1.php Basics of Space Flight, Sec. 1 Ch. 4, NASA Jet Propulsion Laboratory
- (en) Anonymous, « The Sabre Engine », Reaction Engines Ltd. (consulté le )
- (en) K.; Tanatsugu Harada, « Development Study on ATREX Engine », Acta Astronautica, vol. 41, no 12, , p. 851–862 (DOI 10.1016/S0094-5765(97)00176-8)
- (en)ESA Portal – ESA and ANU make space propulsion breakthrough
- (en)« http://pdf.aiaa.org/preview/CDReadyMJPC2005_1177/PV2005_4260.pdf »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) A Xenon Resistojet Propulsion System for Microsatellites (Surrey Space Centre, University of Surrey, Guildford, Surrey)
- (en)Alta - Space Propulsion, Systems and Services - Field Emission Electric Propulsion
- (en)RD-701
- (en)Google Translate
- (en)RD-0410
- (en)Young Engineers' Satellite 2
- (en)Gnom
- (en)NASA GTX
- (en)The PIT MkV pulsed inductive thruster
- (en)« Pratt & Whitney Rocketdyne Wins $2.2 Million Contract Option for Solar Thermal Propulsion Rocket Engine »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (Press release, June 25, 2008, Pratt & Whitney Rocketdyne)
- (en) Robert R. Brownlee, « Operation Plumbbob » (consulté le )










































