Parité d'une fonction
En mathématiques, la parité d'une fonction d'une variable réelle, complexe ou vectorielle est une propriété qui requiert d'abord la symétrie du domaine de définition par rapport à l'origine, puis s'exprime par l'une ou l'autre des relations suivantes :
- fonction paire : pour tout x du domaine de définition, f (−x) = f (x) ;
- fonction impaire : pour tout x du domaine de définition, f (−x) = −f (x).
En analyse réelle, les fonctions paires sont les fonctions dont la courbe représentative est symétrique par rapport à l'axe des ordonnées, telles les fonctions constantes, la fonction carré et plus généralement les fonctions puissance d'exposant pair[1], les fonctions cosinus et cosinus hyperbolique… Les fonctions impaires sont celles dont la courbe représentative est symétrique par rapport à l'origine, telles les fonctions identité, cube et plus généralement les fonctions puissances d'exposant impair, les fonctions inverse, sinus, tangente, sinus hyperbolique et tangente hyperbolique et leurs réciproques.
Les seules fonctions à être à la fois paires et impaires sont les fonctions nulles sur un domaine symétrique.
Une fonction quelconque n'est en général ni paire ni impaire, même si son domaine de définition est symétrique par rapport à l'origine. Toute fonction définie sur un tel domaine s'écrit en revanche de manière unique comme somme d'une fonction paire et d'une fonction impaire.
La mise en évidence de la parité d'une fonction d'une variable réelle (qu'elle soit paire ou impaire) permet notamment de limiter son étude aux réels positifs.
Utilisation[modifier | modifier le code]
La parité des fonctions sert, par exemple, à n'étudier les fonctions que sur la moitié de leur intervalle de définition, l'autre moitié étant déduite par symétrie. On remarquera qu'une fonction impaire, définie en 0, est nulle en ce point (en effet, puisque est impaire, pour tout , et donc ; ainsi .
On peut aussi simplifier le calcul intégral dans le cas de fonction paire ou impaire, puisque pour paire est égale à , ce que l'on visualise bien avec la représentation graphique de l'aire sous la courbe, et respectivement pour impaire est égale à . En effet, il y aura une aussi grande aire positive de à que d'aire négative de à .
Cette définition de parité et d'imparité peut être également explicitée avec la notion de symétrisée d'une fonction : la fonction symétrisée d'une fonction s est la fonction š qui associe à un donné et, par exemple, s est paire si elle est égale à sa symétrisée.
Partie paire et partie impaire d'une fonction[modifier | modifier le code]
Si est un sous-ensemble de symétrique par rapport à 0 (c'est-à-dire que si appartient à alors appartient à ), toute fonction peut se décomposer de façon unique comme somme d'une fonction paire et d'une fonction impaire :
- ,
- où la fonction paire est
- et la fonction impaire est
- .
En effet[2], le sous-espace vectoriel des fonctions paires et celui des fonctions impaires sont supplémentaires dans l'espace des fonctions de dans .
Par conséquent, on peut parler de la partie paire de et de sa partie impaire. Par exemple, la fonction exponentielle se décompose comme somme des fonctions cosinus hyperbolique, et sinus hyperbolique, .
Représentation graphique[modifier | modifier le code]
Soit une fonction définie sur et son graphe, dans un repère d'axes .
- est une fonction paire si et seulement si est symétrique par rapport à l'axe , parallèlement à l'axe .
- est une fonction impaire si et seulement si est symétrique par rapport à l'origine .
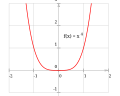
-
La fonction est paire.
-
La fonction est impaire.
Mais une fonction dont la courbe représentative possède un axe ou un centre de symétrie n'est pas forcément paire ou impaire : il est nécessaire que le centre soit ou l'axe soit .
Quelques propriétés[modifier | modifier le code]
- Toute fonction constante est paire.
- Toute fonction paire et monotone sur son ensemble de définition est constante.
- La seule fonction qui soit à la fois paire et impaire est la fonction nulle (fonction constante égale à zéro).
- En général, la somme d'une fonction paire et une fonction impaire n'est ni paire ni impaire ; ex : .
- La somme ou la différence de deux fonctions paires est paire.
- La somme ou la différence de deux fonctions impaires est impaire.
- La parité suit, pour le produit ou le quotient, la règle des signes : tout produit ou quotient de deux fonctions paires est une fonction paire, tout produit ou quotient de deux fonctions impaires est aussi une fonction paire, tout produit ou quotient d'une fonction paire par une fonction impaire est une fonction impaire.
- La dérivée d'une fonction paire dérivable est une fonction impaire ; la dérivée d'une fonction impaire dérivable est une fonction paire.
- Une primitive d'une fonction impaire continue sur E n'est pas forcément paire, sauf si E est un intervalle.
- Une primitive d'une fonction paire continue sur E n'est pas forcément impaire, sauf si E est un intervalle et si de plus la primitive considérée est celle qui s'annule en 0.
- La composée de deux fonctions impaires est impaire ; la composée g ∘ f d'une fonction paire g avec une fonction impaire f est une fonction paire.
- La composée g ∘ f d'une fonction quelconque g avec une fonction paire f est une fonction paire.
Voir aussi[modifier | modifier le code]
Notes et références[modifier | modifier le code]
- Ce qui est probablement une des raisons de ce choix de vocabulaire.
- La preuve par analyse-synthèse est classique et n'est qu'un cas particulier de diagonalisation d'une symétrie : voir par exemple X. Oudot et M. Allano-Chevalier, Mathématiques PCSI-PTSI 1re année : Tout en un, Hachette, (lire en ligne), chap. 11 (« Espaces vectoriels »), p. 203 et .