Modèle macro-économique
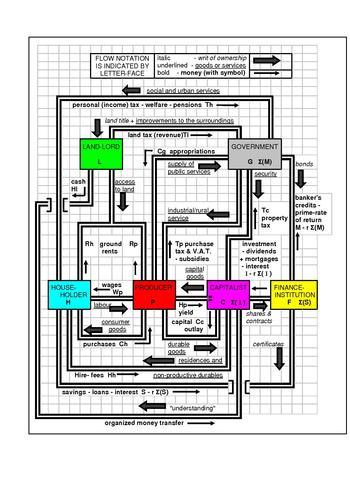
Un modèle macro-économique (ou macroéconomique) est un outil d'analyse destiné à décrire le fonctionnement de l'économie d'un pays ou d'une région. Ces modèles sont généralement conçus pour étudier la dynamique de quantités globales telles que la quantité totale de biens et services produits, le total des revenus, le niveau d'emploi des ressources productives, et le niveau des prix.
Les modèles macro-économiques peuvent être logiques, mathématiques ou numériques ; les différents types de modèles macro-économiques servent à des fins différentes et ont différents avantages et inconvénients[1]. Ils peuvent être utilisés pour préciser et illustrer les principes théoriques de base, pour tester, comparer et quantifier les différentes théories macro-économiques, pour produire des scénarios what if (généralement pour prédire les effets des changements monétaire, budgétaire ou d'autres politiques macro-économiques) ou encore pour générer des prévisions économiques. Ainsi, les modèles macro-économiques sont largement utilisés dans le milieu universitaire, d'enseignement et de recherche et sont aussi largement utilisés par les organisations internationales, les gouvernements et les grandes entreprises, ainsi que par des consultants en économie et des groupes de réflexion.
Types[modifier | modifier le code]
Modèles théoriques simples[modifier | modifier le code]
Des descriptions simples de manuels de la macro-économie impliquant un petit nombre d'équations ou de diagrammes sont souvent appelées « modèles ». Les exemples comprennent le modèle IS-LM et le modèle Mundell-Fleming de la macroéconomie keynésienne, et le modèle de Solow de la théorie de la croissance néoclassique. Ces modèles partagent plusieurs caractéristiques. Ils sont basés sur quelques équations comportant quelques variables, qui peuvent être expliqué avec de simples schémas[2]. La plupart de ces modèles sont statiques, mais certains sont dynamiques, décrivant l'économie sur plusieurs périodes. Les variables qui apparaissent dans ces modèles représentent souvent des agrégats macro-économiques (tels que le PIB ou le total de l'emploi) plutôt que des variables de choix individuelles et bien que les équations reliant ces variables décrivent des décisions économiques, elles ne sont généralement pas dérivées directement de modèles individuels. Ils sont assez simples pour être utilisés comme illustrations de points théoriques dans les explications introductives des idées macroéconomiques ; par conséquent, l'application quantitative à la prévision, aux essais ou à l'évaluation des politiques est habituellement impossible sans augmenter substantiellement la structure du modèle.
Empirique des modèles de prévision[modifier | modifier le code]
Dans les années 1940 et 1950, alors que les gouvernements commençaient à accumuler des données sur le revenu national et la comptabilité des produits, les économistes ont entrepris de construire des modèles quantitatifs pour décrire la dynamique observée dans les données[3]. Ces modèles ont estimé les relations entre différentes variables macroéconomiques à l'aide d'une analyse de séries temporelles (principalement linéaire). Comme les modèles théoriques plus simples, ces modèles empiriques décrivaient les relations entre les quantités agrégées, mais beaucoup traitaient d'un niveau de détail beaucoup plus fin (par exemple, étudier les relations entre la production, l'emploi, l'investissement et d'autres variables).Ainsi, ces modèles ont augmenté pour inclure des centaines ou des milliers d'équations décrivant l'évolution de centaines ou de milliers de prix et de quantités au fil du temps, rendant les ordinateurs essentiels pour leur solution. Alors que le choix des variables à inclure dans chaque équation était en partie guidé par la théorie économique (par exemple, le revenu passé comme déterminant de la consommation, comme suggéré par la théorie des anticipations adaptatives), l'inclusion variable était principalement déterminée empiriquement[4].
L'économiste néerlandais Jan Tinbergen a développé le premier modèle national complet, qu'il a construit pour les Pays-Bas en 1936.Il a ensuite appliqué la même structure de modélisation aux économies des États-Unis et du Royaume-Uni. Le premier modèle macroéconomique mondial, le projet LINK de Wharton Econometric Forecasting Associates, a été initié par Lawrence Klein. Le modèle a été cité en 1980 lorsque Klein, comme Tinbergen avant lui, a remporté le prix Nobel. Des modèles empiriques à grande échelle de ce type, y compris le modèle de Wharton, sont encore utilisés aujourd'hui, en particulier à des fins de prévision[5],[6],[7].
La critique de Lucas sur les modèles de prévision empiriques[modifier | modifier le code]
Les études économétriques dans la première partie du 20e siècle ont montré une corrélation négative entre l'inflation et le chômage appelé la courbe de Phillips[8]. Les modèles empiriques de prévision macroéconomique, basés sur les mêmes données à peu près, ont des implications similaires : ils suggèrent que le chômage pourrait être réduit de façon permanente en augmentant de façon permanente l'inflation.Toutefois, en 1968, Milton Friedman[9] et Edmund Phelps[10] ont fait valoir que ce compromis apparent était illusoire. Ils ont affirmé que la relation historique entre l'inflation et le chômage était due au fait que les épisodes inflationnistes passés avaient été en grande partie inattendus. Ils ont fait valoir que si les autorités monétaires augmentaient de façon permanente le taux d'inflation, les travailleurs et les entreprises finiraient par comprendre cela, à tel point que l'économie retrouverait son précédent niveau de chômage plus élevé, mais maintenant aussi l'inflation. La stagflation des années 1970 est apparu à supporter leur prédiction[11].
En 1976, Robert Lucas, Jr., a publié un article influent affirmant que l'échec de la courbe de Phillips dans les années 1970 n'était qu'un exemple d'un problème général avec les modèles empiriques de prévision[12],[13]. Il a souligné que ces modèles sont dérivés des relations observées entre diverses quantités macroéconomiques dans le temps, et que ces relations diffèrent selon le régime de politique macroéconomique en place. Dans le contexte de la courbe de Phillips. cela signifie que la relation entre l'inflation et le chômage observée dans une économie où l'inflation a généralement été faible, dans le passé, serait différente de la relation observée dans une économie où l'inflation a été élevée[14]. De plus, cela signifie que l'on ne peut pas prédire les effets d'un nouveau régime politique en utilisant un modèle empirique de prévision basé sur des données des périodes précédentes où ce régime politique n'était pas en place. Lucas a soutenu que les économistes resteraient incapables de prédire les effets des nouvelles politiques à moins de construire des modèles basés sur les fondamentaux économiques (comme les préférences, la technologie et les contraintes budgétaires) qui ne devraient pas être affectés par les changements de politique.
Modèles d'équilibre général stochastique dynamique[modifier | modifier le code]
En partie en réponse à la critique de Lucas, les économistes des années 1980 et 1990 ont commencé à construire des modèles macro-économiques fondés sur des choix rationnels, appelés modèles dynamiques d'équilibre général stochastique (DSGE). Ces modèles commencent par spécifier l'ensemble des agents actifs dans l'économie, tels que les ménages, les entreprises et les gouvernements dans un ou plusieurs pays, ainsi que les préférences, la technologie et la contrainte budgétaire de chacun. Chaque agent est supposé faire un choix optimal, en tenant compte des prix et des stratégies des autres agents, à la fois dans la période actuelle et dans le futur. Résumant les décisions des différents types d'agents, il est possible de trouver les prix qui égalent l'offre et la demande sur tous les marchés. Ces modèles incarnent donc une sorte d'auto-consistance d'équilibre: les agents choisissent de manière optimale compte tenu des prix, tandis que les prix doivent être cohérents avec les offres et les demandes des agents.
Les modèles DSGE supposent souvent que tous les agents d'un type donné sont identiques (c'est-à-dire « ménage représentatif » et « entreprise représentative ») et peuvent effectuer des calculs parfaits qui prévoient correctement l'avenir en moyenne (ce que l'on appelle des anticipations rationnelles). Cependant, ce ne sont que des hypothèses simplificatrices et elles ne sont pas essentielles pour la méthodologie DSGE; De nombreuses études DSGE visent un plus grand réalisme en considérant des agents hétérogènes[15], myopes, ou différents types d'anticipations adaptatives[16]. D'autres hypothèses réalistes sont effectuées comme la préférence pour la détention monétaire ou l'aversion au risque variable dans le temps. Comparés aux modèles empiriques de prévision, les modèles DSGE ont généralement moins de variables et d'équations, principalement parce que les modèles DSGE sont plus difficiles à résoudre, même avec l'aide d'ordinateurs[17]. Des modèles DSGE théoriques simples, n'impliquant que quelques variables, ont été utilisés pour analyser les forces qui déterminent les cycles économiques; ce travail empirique a donné lieu à deux principaux cadres concurrents appelé le modèle du cycle économique réel[18],[19],[20] et le nouveau modèle DSGE keynésien[21],[22]. Des modèles DSGE plus élaborés sont utilisés pour prédire les effets des changements de politique économique et évaluer leur impact sur le bien-être social. Cependant, les prévisions économiques reposent encore largement sur des modèles empiriques plus traditionnels, qui sont encore largement considérés comme permettant de prédire avec plus de précision l'impact des perturbations économiques au fil du temps. De nombreuses banques centrales utilisent les modèles DSGE dans le but d'analyser l'économie, les phénomènes passés mais aussi évaluer le futur de manière structurelle ce que les modèles statistiques et empiriques ne permettent pas.
Modèles DSGE versus CGE[modifier | modifier le code]
Une méthodologie étroitement liée qui est antérieure à la modélisation DSGE est la modélisation de l'équilibre général calculable (CGE). Cependant, les modèles EGC se concentrent principalement sur les relations à long terme, ce qui les rend plus aptes à étudier l'impact à long terme de politiques permanentes telles que le système fiscal ou l'ouverture de l'économie au commerce international[23],[24]. Les modèles DSGE mettent plutôt l'accent sur la dynamique de l'économie au fil du temps (souvent à une fréquence trimestrielle), ce qui les rend aptes à étudier les cycles économiques et les effets cycliques de la politique monétaire et budgétaire.
Modèles macroéconomiques computationnels basés sur l'agent[modifier | modifier le code]
Une autre méthodologie de modélisation qui s'est développée en même temps que les modèles DSGE est l'ACE (Agent-based computational economics), qui est une variété de modélisation basée sur l'Agent[25]. Comme la méthodologie DSGE, ACE cherche à décomposer les relations macroéconomiques agrégées en décisions microéconomiques des agents individuels. Les modèles ACE commencent également par définir l'ensemble des agents qui composent l'économie, et spécifient les types d'interactions que les agents individuels peuvent avoir entre eux ou avec le marché dans son ensemble. Au lieu de définir les préférences de ces agents, les modèles ACE sautent souvent directement à la spécification de leurs stratégies. Ou parfois, des préférences sont spécifiées, ainsi qu'une stratégie initiale et une règle d'apprentissage selon lesquelles la stratégie est ajustée en fonction de son succès passé[26]. Compte tenu de ces stratégies, l'interaction d'un grand nombre d'agents individuels (qui peuvent être très hétérogènes) peut être simulée sur un ordinateur, puis les relations agrégées, macroéconomiques qui découlent de ces actions individuelles peuvent être étudiées..
Points forts et points faibles des modèles DSGE et ACE[modifier | modifier le code]
Les modèles DSGE et ACE ont des avantages et des inconvénients différents en raison de leurs structures sous-jacentes différentes. Les modèles DSGE peuvent exagérer la rationalité et la prévoyance individuelles, et sous-estimer l'importance de l'hétérogénéité, puisque les attentes rationnelles, le cas des agents représentatifs, restent le type de modèle DSGE le plus simple et donc le plus commun à résoudre. De même, contrairement aux modèles ACE, il peut être difficile d'étudier les interactions locales entre agents individuels dans les modèles DSGE, qui se concentrent plutôt sur la manière dont les agents interagissent à travers les prix agrégés. D'autre part, les modèles ACE peuvent exagérer les erreurs dans la prise de décision individuelle, puisque les stratégies supposées dans les modèles ACE peuvent être très loin des choix optimaux à moins que le modélisateur soit très prudent. Une question connexe est que les modèles ACE qui partent de stratégies plutôt que de préférences peuvent rester vulnérables à la critique de Lucas : un régime politique modifié devrait généralement donner lieu à des stratégies modifiées.
Liste de modèles macro-économiques[modifier | modifier le code]
- IS-LM
- Mundell-Fleming (IS-LM-BP)
- OG-DG
- IS-PC-MR
- WS-PS
- Solow-Swan
- Harrod-Domar
- New Area-Wide Model
- ECB-MC
- FRB-US
Références[modifier | modifier le code]
- Blanchard, Olivier (2017), The need for different classes of macroeconomic models, blog post, Jan. 12, 2017, Peterson Institute for International Economics.
- Blanchard, Olivier (2000), Macroeconomics, 2nd ed., Chap. 3.3, p. 47. Prentice Hall, (ISBN 0-13-013306-X).
- Lawrence Klein, « The contribution of Jan Tinbergen to economic science », De Economist, vol. 152, no 2, , p. 155–157 (DOI 10.1023/B:ECOT.0000023251.14849.4f)
- Tjalling C. Koopmans, « Measurement Without Theory », Review of Economics and Statistics, vol. 29, no 3, , p. 161–172 (JSTOR 1928627)
- (en) Comparative Performance of US Econometric Models, New York/Oxford, Oxford University Press, , 325 p. (ISBN 0-19-505772-4, lire en ligne)
- Otto Eckstein, The DRI Model of the US Economy, McGraw-Hill, , 253 p. (ISBN 0-07-018972-2)
- Ronald Bodkin, Lawrence Klein et Kanta Marwah, A History of Macroeconometric Model Building, Edward Elgar,
- A. W. Phillips, « The relationship between unemployment and the rate of change of money wages in the United Kingdom 1861-1957 », Economica, vol. 25, (DOI 10.2307/2550759)
- Milton Friedman, The role of monetary policy, vol. 58, American Economic Association, , 1–17 p. (JSTOR 1831652), chap. 1
- Edmund S. Phelps, Money wage dynamics and labor market equilibrium, vol. 76, , 678–711 p. (DOI 10.1086/259438), chap. 4
- Blanchard, Olivier (2000), op. cit., Ch. 28, p. 540.
- Robert E., Jr. Lucas, Econometric Policy Evaluation : A Critique, vol. 1, , 19–46 p. (DOI 10.1016/S0167-2231(76)80003-6)
- (en) Kevin D. Hoover, The New Classical Macroeconomics, Oxford, Basil Blackwell, , 167–209 p. (ISBN 0-631-14605-9), « Econometrics and the Analysis of Policy »
- Blanchard, Olivier (2000), op. cit., Ch. 28, p. 542.
- Per Krusell et Anthony A., Jr. Smith, « Income and wealth heterogeneity in the macroeconomy », Journal of Political Economy, vol. 106, no 5, , p. 243–277 (DOI 10.1086/250034)
- George W. Evans and Seppo Honkapohja (2001), Learning and Expectations in Macroeconomics. Princeton University Press, (ISBN 0-691-04921-1).
- DeJong, D. N. with C. Dave (2007), Structural Macroeconometrics. Princeton University Press, (ISBN 0-691-12648-8).
- Finn E. Kydland et Edward C. Prescott, « Time to Build and Aggregate Fluctuations », Econometrica, vol. 50, , p. 1345–70 (DOI 10.2307/1913386)
- Thomas F. Cooley (1995), Frontiers of Business Cycle Research. Princeton University Press.
- Andrew Abel and Ben Bernanke (1995), Macroeconomics, 2nd ed., Ch. 11.1, pp. 355-362. Addison-Wesley, (ISBN 0-201-54392-3).
- Julio J. Rotemberg et Michael Woodford, « An optimization-based econometric framework for the evaluation of monetary policy », NBER Macroeconomics Annual, vol. 12, , p. 297–346 (JSTOR 3585236)
- Michael Woodford, Interest and Prices : Foundations of a Theory of Monetary Policy, Princeton University Press, , 808 p. (ISBN 0-691-01049-8)
- John B. Shoven et John Whalley, « A general equilibrium calculation of the effects of differential taxation of income from capital in the US », Journal of Public Economics, vol. 1, nos 3–4, , p. 281–321 (DOI 10.1016/0047-2727(72)90009-6)
- Patrick J. Kehoe et Timothy J. Kehoe, « A primer on static applied general equilibrium models », Federal Reserve Bank of Minneapolis Quarterly Review, vol. 18, no 1, , p. 2–16 (lire en ligne)
- Leigh Tesfatsion, « Agent-based computational economics », Scholarpedia, vol. 2, no 2, , p. 1970 (ISSN 1941-6016, DOI 10.4249/scholarpedia.1970, lire en ligne)
- William A. Brock et Cars H. Hommes, « A Rational Route to Randomness », Econometrica, vol. 65, no 5, , p. 1059 (ISSN 0012-9682, DOI 10.2307/2171879, lire en ligne)

