Aller au contenu

Diagramme d'Euler

Un article de Wikipédia, l'encyclopédie libre.

Pour un article plus général, voir Diagrammes d'Euler, de Venn et de Carroll.

Un diagramme d'Euler illustrant que l'ensemble des « animaux à quatre pattes » est un sous-ensemble des « animaux », mais l'ensemble des « minéraux » est disjoint (il n'a pas de membres en commun) avec « animaux ».

Un diagramme d'Euler est un moyen de représentation diagrammatique des ensembles et des relations en leur sein. La première utilisation des « cercles Eulériens » est communément attribuée au mathématicien suisse Leonhard Euler (1707-1783). Ils sont étroitement liés aux diagrammes de Venn, mathématicien britannique (1834–1923).

Les diagrammes de Venn et d'Euler ont été incorporés à l'enseignement de la théorie des ensembles dans le cadre des mathématiques modernes dans les années 1960. Depuis lors, ils ont également été adoptés dans d'autres domaines du programme d'études tels que la lecture[1].

Aperçu

[modifier | modifier le code]
Les 22 (des 256) diagrammes de Venn essentiellement différents avec 3 cercles (en haut) et leurs diagrammes d'Euler correspondant (en bas).
Certains des diagrammes d'Euler ne sont pas caractéristiques, et certains sont même équivalents aux diagrammes de Venn. Les zones sont ombrées pour indiquer qu'elles ne contiennent aucun élément.

Les diagrammes d'Euler sont constitués de simples courbes fermées (habituellement des cercles) dans le plan qui représentent les ensembles. Les tailles ou formes des courbes ne sont pas importantes : la signification du diagramme est dans la façon dont les cercles se chevauchent. Les relations spatiales entre les régions délimitées par chaque courbe correspondent aux relations théoriques à ensembles (intersection, sous-ensembles et disjonction).

Chaque courbe d'Euler divise le plan en deux régions ou « zones » : l'intérieur, ce qui représente symboliquement les éléments contenus dans l'ensemble, et l'extérieur, qui représente tous les éléments qui ne sont pas membres de l'ensemble. Les courbes dont les zones intérieures ne se coupent pas représentent des ensembles disjoints. Deux courbes dont les zones intérieures se croisent représentent des ensembles qui ont des éléments communs ; la zone à l'intérieur de deux courbes représente l'ensemble des éléments communs aux deux ensembles (l'intersection des ensembles). Une courbe qui est entièrement contenue à l'intérieur de la zone intérieure d'une autre représente un sous-ensemble de celle-ci.

Exemples de petits diagrammes de Venn (à gauche) avec les régions ombragées représentant des ensembles vides, montrant comment ils peuvent être facilement transformés en diagrammes d'Euler (à droite).

Les diagrammes de Venn sont une forme plus restrictive des diagrammes d'Euler. Un diagramme de Venn doit contenir 2n zones possibles correspondant au nombre de combinaisons d'inclusion ou d'exclusion dans chacun des ensembles. Les régions qui ne font pas partie de l'ensemble sont indiqués par la couleur noir, contrairement aux diagrammes d'Euler, où l'appartenance à l'ensemble est indiquée par le chevauchement ainsi que la couleur. Lorsque le nombre d'ensembles devient supérieur à 3, un diagramme de Venn devient visuellement complexe, en particulier par rapport au diagramme d'Euler correspondant. La différence entre les diagrammes de Venn et d'Euler peut être vue dans l'exemple suivant. Soit trois ensembles :

Les diagrammes de Venn et d'Euler de ces ensembles sont :

  • Diagramme d'Euler
    Diagramme d'Euler
  • Diagramme de Venn
    Diagramme de Venn

Dans un cadre logique, on peut utiliser la sémantique théorique pour interpréter les diagrammes d'Euler, dans un univers du discours. Dans les exemples ci-dessus, le diagramme d'Euler montre que les ensembles Animal et Minéral sont disjoints puisque les courbes correspondantes sont disjointes, et que l'ensemble Quatre Pattes est un sous-ensemble de l'ensemble des Animal. Le diagramme de Venn, qui utilise les mêmes catégories Animal, Minéral, et Quatre Pattes, n'inclut pas ces relations. Traditionnellement le vide d'un ensemble dans un diagrammes de Venn est représenté par l'ombrage de la région concernée. Les diagrammes d'Euler représentent le vide, soit par l'ombrage, soit par l'absence de la région.

Histoire

[modifier | modifier le code]

Sir William Hamilton, dans son livre publié à titre posthume Lectures on Metaphysic and Logic (1858-1860) affirme que l'utilisation des cercles dans le but de « rendre compréhensible... les abstractions de la Logique » (p. 180) ne venait pas de Leonhard Paul Euler (1707-1783), mais plutôt de Christian Weise (en) (1642-1708) dans son Nucleus Logicae Weisianae qui est paru en 1712 à titre posthume. Il fait référence à des lettres d'Euler à une princesse allemande [Partie ii., Lettre XXXV., Éd. Cournot. - ED][2].

Dans Symbolic Logic de 1881, au chapitre V (« Représentation diagrammatique »), John Venn commente sur la prévalence remarquable du diagramme d'Euler :

« Des soixante premiers traités logiques, publiés au cours du dernier siècle, qui ont été consultés à cet effet : - quelque peu au hasard, comme ils se trouvaient les plus accessibles : - il est apparu que trente quatre font appel à l'aide de diagrammes, la quasi-totalité de ceux-ci faisant usage du diagramme Eulérien. »

— (Note 1 p. 100)

Néanmoins, il a soutenu « l'inapplicabilité de ce diagramme pour les besoins d'une logique très générale » (p. 100). Venn termine son chapitre avec l'observation illustrée dans les exemples ci-dessous, que leur utilisation est basée sur la pratique et l'intuition, non pas sur une pratique algorithmique stricte :

« En fait... ces diagrammes non seulement ne correspondent pas avec (sic) le schéma ordinaire, mais ne semblent pas avoir de système reconnu de propositions auxquelles ils pourraient être constamment affiliés. »

— (p. 124-125)

Dans l'usage moderne, le diagramme de Venn comprend une « boîte » qui entoure tous les cercles et représente l'univers du discours.

Couturat observe maintenant que, dans une algorithmique (systématique formelle) de manière directe, on ne peut pas tirer d'équations booléennes réduites, ni de démonstration à la conclusion « Aucun X n'est Z ». Couturat a conclu que le processus « a... de sérieux inconvénients en tant que méthode servant à résoudre des problèmes logiques » :

« Il ne montre pas comment les données sont exposées en annulant certains constituants, ni comment combiner les constituants restants de manière à obtenir les conséquences recherchées. En bref, il ne sert qu'à présenter une seule étape d'un argument, à savoir l'équation du problème. Ainsi, il est très peu utile, dans la mesure où les constituants peuvent être représentés par des symboles algébriques tout aussi bien que par des régions, et sont beaucoup plus faciles à traiter sous cette forme. »

— (p. 75)

En 1952, Maurice Karnaugh adapte et développe une méthode proposée par Edward W. Veitch (en) ; ce travail se fonde sur la méthode des tables de vérité précisément définies en 1921 dans la thèse d'Emil Post Introduction à une théorie générale des propositions élémentaires et l'application de la logique propositionnelle à la logique des circuits par (entre autres) Claude Shannon, George Stibitz (en) et Alan Turing. Par exemple, dans le chapitre « Boolean Algebra », Hill et Peterson (1968, 1964) présentent les sections[pas clair] 4.5ff « théorie des ensembles comme un exemple de l'algèbre de Boole » et en elle[pas clair], ils présentent le diagramme de Venn avec l'ombrage. Ils donnent des exemples de diagrammes de Venn pour résoudre, par exemple, des problèmes de circuit, mais finissent avec cette déclaration :

« Pour un nombre de variables supérieur à trois, la forme illustrative du diagramme de Venn ne convient plus. Des extensions sont possibles, cependant, le plus commode est la table de Karnaugh, à discuter dans le chapitre 6. »

— (p. 64)

Dans le chapitre 6, section 6.4 (« Karnaugh Map Representation of Boolean Functions »), ils commencent par :

« L'application de Karnaugh1 [1Karnaugh 1953] est l'un des outils les plus puissants du répertoire de la logique.... Une table de Karnaugh peut être considérée soit comme une forme picturale d'une table de vérité, soit comme une extension du diagramme de Venn. »

— (p. 103-104)

L'histoire du développement par Karnaugh de sa table est obscure. Karnaugh, dans son article de 1953, référence Veitch 1951[réf. souhaitée], Veitch référence Shannon 1938 (essentiellement la thèse de master de Shannon au M. I. T.), et Shannon à son tour renvoie, entre autres auteurs de textes logiques, à Couturat 1914. Dans la méthode de Veitch, les variables sont disposées dans un rectangle ou un carré ; comme décrit dans la table de Karnaugh, Karnaugh a changé l'ordre des variables dans sa méthode pour correspondre à ce qui est maintenant connu sous le nom d'hypercube.

Exemple : diagramme d'Euler à Venn et table de Karnaugh

[modifier | modifier le code]

Cet exemple montre les diagrammes d'Euler de Venn et de Karnaugh vérifier la déduction « aucun X n'est Z ». Dans le tableau ci-dessous, les symboles logiques suivants sont utilisés :

1 peut être lu comme « vrai », 0 comme « faux » ;
~ pour NON et abrégé en '. Par exemple x' =défini NON x ;
+ pour le OU logique (de l'algèbre de Boole : 0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 1) ;
& (ET logique) entre propositions ; il est parfois omis de la même manière que le signe de la multiplication : par exemple x'y'z =défini ~x & ~y & z (de l'algèbre de Boole : 0*0 = 0, 0*1 = 0, 1*0 = 0, 1*1 = 1, où * figure pour plus de clarté) ;
→ (IMPLICATION logique) : à lire SI... ALORS..., ou « IMPLIQUE », P → Q =défini NON P OU Q.

Compte tenu de la conclusion proposée comme « Aucun X n'est Z », on peut tester si une déduction est correcte par l'utilisation d'une table de vérité. La méthode la plus simple est de mettre la formule à gauche (abrégez "P") et mettre la déduction (possible) sur la droite (abrégez "Q") et les connecter grâce à l'implication logique, à savoir P → Q, lu comme SI P ALORS Q. Si l'évaluation de la table de vérité ne produit que des 1 sous le signe de l'implication alors P → Q est une tautologie. Étant donné ce fait, on peut « détacher » la formule de droite de la manière décrite sous la table de vérité.

Compte tenu de l'exemple ci-dessus, la formule pour les diagrammes d'Euler et de Venn est :

« Aucun Y n'est Z » et « Tout X est Y » : ( ~(y & z) & (x → y) ) =défini P

et la déduction proposée est :

« Aucun X n'est Z » : ( ~ (x & z) ) =défini Q

Alors maintenant, la formule à évaluer peut être abrégée :

( ~(y & z) & (x → y) ) → ( ~ (x & z) ): P → Q
SI (« Aucun Y n'est Z » et « Tout X est Y ») ALORS (« Aucun X n'est Z »).
La table de vérité montre que la formule ( ~(y & z) & (x → y) ) → ( ~ (x & z) ) est une tautologie, comme indiqué par tous les 1 sur la colonne jaune
 # Venn, Karnaugh  x y z (~ (y & z) & (x → y)) → (~ (x & z))
0 x'y'z' 0 0 0 1 0 0 0 1 0 1 0 1 1 0 0 0
1 x'y'z 0 0 1 1 0 0 1 1 0 1 0 1 1 0 0 1
2 x'yz' 0 1 0 1 1 0 0 1 0 1 1 1 1 0 0 0
3 x'yz 0 1 1 0 1 1 1 0 0 1 1 1 1 0 0 1
4 xy'z' 1 0 0 1 0 0 0 0 1 0 0 1 1 1 0 0
5 xy'z 1 0 1 1 0 0 1 0 1 0 0 1 0 1 1 1
6 xyz' 1 1 0 1 1 0 0 1 1 1 1 1 1 1 0 0
7 xyz 1 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1

À ce stade, l'implication ci-dessus P → Q (~(y & z) & (x → y) ) → ~(x & z) ) est encore une formule, et la déduction – le « détachement » de Q de P → Q – n'a pas eu lieu. Mais étant donné la démonstration selon laquelle P → Q est une tautologie, l'étape suivante est la procédure du modus ponens afin de « détacher » Q : « Aucun X n'est Z » et de distribuer les termes sur la gauche.

Le Modus ponens (ou « règle fondamentale de l'inférence[3] ») est souvent noté comme suit : les deux termes sur la gauche, « P → Q » et « P », sont appelés prémisses (par convention liées par une virgule), le symbole ⊢ signifie « prouve » (dans le sens de la déduction logique), et le terme de droite est appelée la conclusion :

P → Q, P ⊢ Q.

Pour que le modus ponens réussisse, les deux prémisses P → Q et P doivent être vraies. Parce que, comme l'a démontré ci-dessus, le prémisse P → Q est une tautologie, la « vérité » est toujours le cas, peu importe les valeurs que prennent x, y et z, mais la « vérité » ne sera le cas pour P dans ces circonstances que lorsque P sera évalué « vrai » (par exemple les colonnes 0 OU 1 OU 2 OU 6 : x'y'z' + x'y'z + x'yz' + xyz' = x'y' + yz')[4].

P → Q , P ⊢ Q
c'est-à-dire : ( ~(y & z) & (x → y) ) → ( ~ (x & z) ) , ( ~(y & z) & (x → y) ) ⊢ ( ~ (x & z) )
c'est-à-dire : SI « Aucun Y n'est Z » et « Tout X est Y » ALORS « Aucun X n'est Z » (« Aucun Y n'est Z » et « Tout X est Y » ⊢ « Aucun X n'est Z »).

On est maintenant libre de « détacher » la conclusion « Aucun X n'est Z », qui peut être utilisée dans une déduction ultérieure.

L'utilisation de l'implication tautologique signifie que d'autres déductions possibles existent en plus de « Aucun X n'est Z ».

Galerie

[modifier | modifier le code]
  • Diagramme de Venn montrant toutes les intersections possibles.
    Diagramme de Venn montrant toutes les intersections possibles.
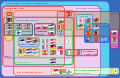
  • Diagramme d'Euler représentant une situation réelle, à savoir les relations entre les différentes organisations européennes supranationales. (Version cliquable)
    Diagramme d'Euler représentant une situation réelle, à savoir les relations entre les différentes organisations européennes supranationales. (Version cliquable)
  • Diagramme humoristique comparant les diagrammes d'Euler et de Venn.
    Diagramme humoristique comparant les diagrammes d'Euler et de Venn.
  • Diagramme d'Euler des types de triangles.
    Diagramme d'Euler des types de triangles.

Notes et références

[modifier | modifier le code]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Euler diagram » (voir la liste des auteurs).
  1. ↑ (en) Raymond C. Jones, Strategies for Reading Comprehension Venn Diagrams, sur readingquest.org.
  2. ↑ Au moment où ces conférences de Hamilton ont été publiées, Hamilton aussi était mort.
  3. ↑ Cf. Reichenbach 1947, p. 64.
  4. ↑ Reichenbach discute du fait que l'implication P → Q n'a pas besoin d'être une tautologie (aussi appelée « implication tautologique »).

Voir aussi

[modifier | modifier le code]

Articles connexes

[modifier | modifier le code]

Bibliographie

[modifier | modifier le code]

Classée par date de publication :

Liens externes

[modifier | modifier le code]
Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Diagramme_d%27Euler&oldid=219971681 ».