Utilisateur:Jean-Christophe BENOIST/EE

L'équation d'Einstein est l'expression mathématique de la Relativité Générale et plus généralement de toute la physique de la gravitation. Il s'agit d'une formule fondamentale, qui ne peut être dérivée d'une théorie sous-jacente dont elle dériverait.

Sa forme générale signifie :

${\biggl (}{\text{Une mesure de la courbure moyenne de l'espace-temps}}{\biggr )}={\biggl (}\mathrm {Une~mesure~de~la~densit{\acute {e}}~d'{\acute {e}}nergie} {\biggr )}$

Cette équation exprime et concentre les idées principales d'Einstein gouvernant la relativité générale : le principe d'équivalence amène à affirmer que la gravitation n'est pas une véritable force. S'il n'existe aucune force pour dévier ou accélérer la trajectoire des objets, c'est que c'est l'espace-temps lui-même qui est déformé et la théorie de la gravitation doit se manifester sous forme d'une courbure de l'espace-temps. Les objets suivent des géodésiques, qui peuvent être considérées comme l'équivalent des lignes droites pour cet espace-temps courbé. L'utilisation du formalisme des tenseurs rend l'expression de cette loi indépendante des référentiels et est donc conforme au principe de relativité.

Cette équation gouverne la manière avec laquelle l'espace-temps se courbe en fonction de la matière et, réciproquement, la matière se dispose ou évolue en fonction de la courbure. L'espace-temps agit sur la matière, qui elle-même agit sur l'espace-temps. Cette rétroaction se traduit par une non-linéarité des équations d'Einstein, qui sont de ce fait extrêmement difficile à résoudre de manière exacte.

Cette équation se traduit par un ensemble complexe d'équations différentielles d'un tenseur métrique $g_{ij}$. Néanmoins l'expression de cette équation reste concise et élégante, et est considérée par beaucoup de physiciens comme étant une des formules les plus importantes et les plus belles de la physique.

Ses solutions, qui sont des métriques de l'espace-temps, permettent de définir des modèles cosmologiques formalisant l'évolution à grande échelle de l'univers, de modéliser les propriétés d'objets astronomiques comme les trous noirs, ou de prédire l'existence d'ondes gravitationnelles. Elle incorpore bien entendu la loi universelle de la gravitation de Newton comme approximation dans le cas de champ gravitationnel faible.

Plus précisément, l'équation d'Einstein s'exprime sous la forme globale suivante :

$G_{ij}=\chi \ T_{ij}$

avec $G_{ij}$ qui est le tenseur d'Einstein qui représente la courbure de l'espace-temps, et $T_{ij}$ qui est le tenseur énergie-impulsion représentant la contribution de toute l'énergie (et donc de la matière par la relation E=mc²) au champ gravitationnel, hors énergie éventuellement présente dans le champ gravitationnel lui-même.

$\chi$ est un simple facteur dimensionnel, permettant d'exprimer l'équation dans les unités usuelles et de faire correspondre l'équation à la réalité physique et à la valeur observée de la constante gravitationnelle.

La manière la plus naturelle de représenter la courbure par un tenseur serait d'utiliser un tenseur de Riemann, qui est la façon la plus courante d'exprimer la courbure des variétés riemanniennes, l'espace-temps étant parfaitement représenté par une variété pseudo-riemannienne). Mais ce tenseur est d'ordre 4 (à 4 indices), alors que le tenseur énergie-impulsion est d'ordre 2 : 2 indices sont en effet suffisants pour décrire toutes les propriétés dynamiques de l'énergie et la matière, et construire un tenseur énergie-impulsion d'ordre 4 n'aurait aucun sens physique. Le tenseur énergie-impulsion possède également une dérivée covariante nulle, qui représente la loi de conservation de l'énergie (locale).

Il est donc nécessaire de construire un tenseur spécial représentant la courbure, ayant un sens physique et qui puisse être identifié au tenseur énergie-impulsion. C'est tout le travail qu'effectue Einstein entre 1913 et 1915, pour aboutir au tenseur d'Einstein, et à la formulation exacte de l'équation d'Einstein.

Le tenseur d'Einstein

Le tenseur de Ricci (composantes rouges) représente l'accélération à partir de l'état de repos d'une sphère de particules entourant une masse.

Le tenseur d'Einstein est donc un tenseur qui, dans l'équation d'Einstein, représente la courbure et possède une signification physique, c'est à dire d'ordre 2, symétrique, possédant une dérivée covariante nulle, et qui permet de retrouver la loi de gravitation de Newton comme approximation avec des champs gravitationnels faibles et vitesses en jeu très inférieures à celle de la lumière.

Il existe un moyen de construire un tenseur d'ordre 2 à partir d'un tenseur d'ordre 4 : effectuer une contraction du tenseur selon deux indices. Une telle contraction du tenseur de Riemann donne un tenseur connu sous le nom de tenseur de Ricci, noté $R_{ij}$. Si le tenseur de Riemann donne la courbure d'une variété en un point, selon un plan défini par un couple de vecteurs, le tenseur de Ricci représente la moyenne des courbures selon tous les plans orthogonaux à un vecteur donné.

Pour construire une équation physique, le tenseur de Ricci possède une propriété intéressante : il permet de retrouver l'accélération à partir de l'état de repos d'une sphère de particules entourant une masse ponctuelle. En mécanique newtonienne, cette même accélération est calculée à partir de l'équation de Poisson ${\nabla }^{2}\Phi =4\pi G\rho$, $\Phi$ étant le potentiel gravitationnel et $\rho$ la densité de masse. Le tenseur de Ricci $R_{ij}$ et le terme gauche de l'équation de Poisson possédant tous les deux des dérivées secondes de la métrique et ayant une même signification physique, il serait naturel de poser :

$G_{ij}=R_{ij}=4\pi GT_{ij}$

$T_{ij}$ étant le tenseur représentant la densité de masse, et cette équation a été effectivement proposée en 1913 par Einstein. Ce tenseur est en effet d'ordre 2 et symétrique, mais il s'avère que sa dérivée covariante n'est pas nulle. En fait, en utilisant les identités de Bianchi sur le tenseur de Riemann, on trouve que c'est le tenseur $R_{ij}\ -\ {\frac {1}{2}}\,g_{ij}\,R$ qui possède une dérivée covariante nulle. Einstein de connaissait pas les identités de Bianchi, et trouve le tenseur d'Einstein, après deux ans d'intense efforts, aidé par le mathématicien Marcel Grossmann :

$G_{ij}=R_{ij}\ -\ {\frac {1}{2}}\,g_{ij}\,R$

$R$ est la courbure scalaire, qui est elle-même une contraction du tenseur de Ricci, et $g_{ij}$ est le tenseur métrique, solution des équation d'Einstein.

Il a été démontré que le tenseur d'Einstein est le seul tenseur pouvant être mathématiquement construit qui possède toutes les propriétés voulues : ordre 2, qui possède des dérivées secondes de la métrique, de dérivée covariante nulle et qui s'annule en espace plat (permettant de retrouver Newton)

David Hilbert a aussi justifié cette équation par le principe de moindre action dès 1915.

Expression complète de l'équation d'Einstein

Étant donné le tenseur d'Einstein, la formulation complète et exacte de l'équation d'Einstein en découle directement :

$\ R_{ij}-{\frac {1}{2}}g_{ij}.R=\chi \ T_{ij}$

avec $\chi ={\frac {8\pi G}{c^{4}}}$, et (i,j) allant de 1 à 4 (pour les 4 dimensions de l'espace-temps).

Éclatée en équations différentielles, cette expression tensorielle se traduit par dix équations aux dérivées partielles non-linéaires. Sur ces dix équation, quatre dépendent du choix du référentiel, ce qui laisse six équations à résoudre pour déterminer la métrique.

Constante cosmologique

Il est important de noter que l'ajout d'une constante au tenseur d'Einstein ne change pas ses caractéristiques physiques : sa dérivée covariante reste nulle et les lois de Newton sont toujours retrouvées aux limites. L’équation du champ peut donc contenir un paramètre « supplémentaire » appelé la constante cosmologique $\ \Lambda$ qui a été introduite à l’origine par Einstein pour qu’un univers statique (c’est-à-dire un univers qui n’est ni en expansion, ni en contraction) soit solution de son équation.

Les équations d'Einstein s'écrivent alors :

$\ R_{ij}-{\frac {1}{2}}g_{ij}.R-g_{ij}.\Lambda =\chi T_{ij}$

Cet effort se solda par un échec pour deux raisons : d'un point de vue théorique, l’univers statique décrit par cette théorie est instable ; et de plus les observations de l’astronome Edwin Hubble dix ans plus tard démontrèrent que l’Univers était en fait en expansion. Donc $\ \Lambda$ fut abandonnée, mais récemment, des techniques astronomiques ont montré qu’une valeur non nulle de ce paramètre permet d'expliquer certaines observations, notamment l'énergie sombre.

Équation d'Einstein dans le vide. Tenseur de Weyl

Il est possible de reformuler les équations d'Einstein de manière, rigoureusement équivalente, à isoler le tenseur de Ricci :

$R_{ij}=\chi \ (T_{ij}-{\frac {1}{2}}g_{ij}.T)+g_{ij}.\Lambda$

Dans le vide où il n'existe aucune énergie ni matière, $T_{ij}=0$. Il devient alors apparent l'équation d'Einstein se résume à :

$R_{ij}=0$

quand la constante cosmologique est nulle. Un espace vide dont le tenseur de Ricci s'annule est nommé un espace "Ricci-plat". Cela ne signifie pas que l'espace-temps est plat en l'absence de toute matière ou énergie : la courbure de l'espace est représenté par le tenseur de Riemann, pas par le tenseur de Ricci.

Déformation d'une sphère de particules soumise aux forces de marée, modélisée par le tenseur de Weyl

Si on considère le tenseur de Ricci comme la source du champ gravitationnel, le champ gravitationnel lui-même est représenté par le tenseur de Riemann, auquel au soustrait le tenseur de Ricci pour ne laisser que les degrés de liberté qui ne sont pas issus de la source elle-même. Le tenseur obtenu est le tenseur de Weyl $C_{ijkl}$, qui a les mêmes propriétés que le tenseur de Riemann, mais qui représente réellement le champ gravitationnel : $WEYL=RIEMANN-RICCI$. C'est l'annulation de ce tenseur qui est la condition pour la platitude conforme de l'espace-temps.

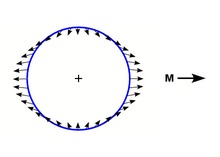
Le tenseur de Weyl représente les forces de marée dues à la gravitation. Une sphère de particules soumise au tenseur de Weyl, par l'influence d'une masse en dehors de la sphère, subit une déformation qui ne change pas son volume, contrairement à l'influence du tenseur de Ricci. Les ondes gravitationnelles sont décrites, dans le vide, par le tenseur de Weyl.

La masse gravitationnelle active

Le tenseur densité-impulsion amène à définir le concept de masse en relativité générale de manière légèrement différente que dans le cas des lois Newtoniennes. En reprenant l'expression de l'équation d'Einstein qui isole le tenseur de Ricci : $R_{ij}=\chi \ (T_{ij}-{\frac {1}{2}}g_{ij}.T)+g_{ij}.\Lambda$, et en identifiant celui-ci à l'accélération initiale, et à l'équation de Poisson, on trouve une masse gravitationnelle active équivalente:

$\rho _{G}=\rho +P_{1}+P_{2}+P_{3}-{\frac {\Lambda }{4\pi G}}$

au lieu de $\rho _{G}=\rho$ dans le cas Newtonien. Les valeurs $P_{i}$ sont les valeurs de la pression sur les trois axes spatiaux orthogonaux, et la constante gravitationnelle contribue à la masse gravitationnelle active.

Dans les conditions normales, les contributions de la pression à la masse gravitationnelle active est très faible, et la constante cosmologique négligeable. Mais la pression peut jouer un rôle considérable dans des conditions extrêmes notamment lors de l'effondrement gravitationnel d'étoiles massives, où la pression - au lieu de s'opposer à l'effondrement gravitationnel comme on pourrait s'y attendre - accroit la tendance à l'effondrement en augmentant la masse gravitationnelle active.