Suite diatomique de Stern

En mathématiques, la suite diatomique de Stern est une suite d'entiers naturels introduite par le mathématicien Moritz Stern en 1858^[1], et dont les premiers termes sont :

0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, … (suite A002487 de l'OEIS).

La n-ième valeur de cette suite est fusc(n), où la fonction fusc est définie par les relations de récurrence suivantes :

fusc(0) = 0
fusc(1) = 1
fusc(2n) = fusc(n)
fusc(2n + 1) = fusc(n) + fusc(n + 1)

L'appellation "fusc" a été donné, sans explication, par Edsger W. Dijkstra en 1976 ^[2]^,^[3].

On peut construire la suite ligne par ligne en procédant selon la figure ci-contre. Omettant le premier terme 0, on part de la ligne 1 - 1. Puis chaque nouvelle ligne est recopiée de la ligne précédente en insérant des nombres, chaque nouveau nombre étant la somme des deux nombres situés de part et d'autre de sa position dans la ligne précédente.

Propriétés

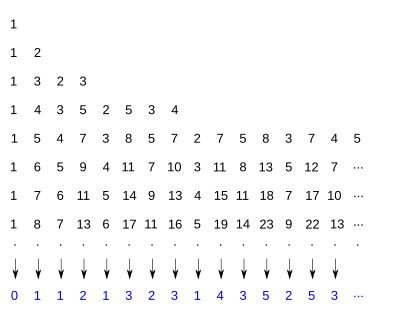
Si l'on dispose la suite de Stern en lignes successives de 1, 2, 4, 8, ... termes, comme dans la figure ci-contre, il apparait des propriétés remarquables.

La somme des termes de chaque ligne est une puissance de 3.
Les maximum de chaque ligne constituent la suite de Fibonacci.
Si on omet le 1 initial, chaque ligne est un palindrome.

Chaque colonne forme une suite arithmétique. La suite formée des raisons est la suite de Stern elle-même. Cela signifie que la suite de Stern dispose d'une structure fractale.

Si l'on décompose l'entier n en binaire : $n=2^{d_{r}}+2^{d_{r-1}}+\dots +2^{d_{0}}$ , les puissances étant décroissantes, alors fusc(n) est égal au déterminant de la matrice tridiagonale^[4] :

${\begin{pmatrix}d_{r}-d_{r-1}+1&1&0&0&\dots &0\\1&d_{r-1}-d_{r-2}+1&1&0&\dots &0\\\vdots &&&\dots &&\vdots \\0&\dots &0&1&d_{2}-d_{1}+1&1\\0&\dots &0&0&1&d_{1}-d_{0}+1\\\end{pmatrix}}$

Par exemple, pour $n=13=2^{3}+2^{2}+2^{0}$ , la matrice est ${\begin{pmatrix}2&1\\1&3\end{pmatrix}}$ , de déterminant fusc(13)=5. Cette propriété permet de montrer que l'entier m obtenu à partir de n en inversant l'ordre de ses chiffres binaires a même image que n par fusc. Ainsi, pour n = 13 = 0b1101, on a m=0b1011 = 11 et fusc(11) = 5.

Structure fractale

La suite de Stern apparaît quand on compte le nombre de coefficients impairs des diagonales ascendantes du triangle de Pascal.

La structure fractale de la suite apparaît également en liaison avec le triangle de Sierpiński. Ce dernier peut se remplir par étape à partir du triangle de Pascal en noircissant les nombres impairs et en blanchissant les nombres pairs. Si on compte les nombres impairs le long des diagonales ascendantes du triangle de Pascal, on obtient la suite de Stern. Dans la figure ci-contre, les nombres impairs ont été remplacés par des 1 et les nombres pairs par des 0. Ce procédé est comparable à l'obtention des termes de la suite de Fibonacci en sommant les termes des diagonales ascendantes du triangle de Pascal.

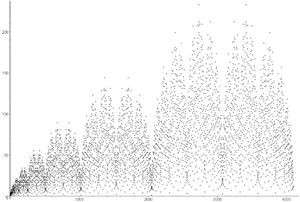
On peut enfin visualiser cet aspect en représentant graphiquement les points (n,fusc(n)) de la suite.

Série génératrice

La série génératrice $G(x)=\sum _{n=0}^{\infty }{\rm {fusc}}(n)x^{n}$ de la suite de Stern est égale à^[5] :

G(x)=x\prod _{n=0}^{\infty }\left(1+x^{2^{n}}+x^{2^{n+1}}\right)

Si on développe cette fonction, on montre que fusc(n+1) est égal au nombre de façon de décomposer n comme somme de puissances de 2 sous la forme suivante, généralisant la notation en système binaire :

n=e_{0}+2e_{1}+4e_{2}+8e_{3}+\dots

où les

e_{i}

valent 0, 1, ou 2.

Par exemple, pour n = 18, fusc(19) = 7, et 18 possède 7 décompositions, à savoir :

18 = 2 + 16 = 1 + 1 + 16 = 2 + 8 + 8 = 1 + 1 + 8 + 8 = 2 + 4 + 4 + 8 = 1 + 1 + 4 + 4 + 8 = 1 + 1 + 2 + 2 + 4 + 8

Dénombrement

La suite de Stern intervient dans plusieurs problèmes de dénombrement.

fusc(n) est le nombre de sous-suites^[6] de la forme 1010...101 (avec une alternance de 1 et de 0, commençant et se terminant par 1, limitée éventuellement à un seul 1) extraites de la suite constituant la décomposition de n en base 2. Par exemple $19=10011_{b}$ en binaire, et il y a fusc(19) = 7 sous-suites possibles, à savoir 4 suites de la forme 101 et 3 suites limitées à 1.

fusc(n) est le nombre de valeurs impaires k pour lesquelles le nombre de Stirling de deuxième espèce $\left\{{\begin{matrix}n\\k\end{matrix}}\right\}$ est lui-même impair^[7]. Par exemple, les nombres de Stirling vérifiant cette propriété pour n = 9 sont 1, 3025, 6951, 1, et fusc(9) = 4.

Suite de Stern et nombres rationnels

La suite de Stern permet d'établir une bijection entre les entiers positifs ou nuls et les nombres rationnels positifs ou nuls au moyen de l'application^[8] :

n\in \mathbb {N} \rightarrow {\frac {{\rm {fusc}}(n)}{{\rm {fusc}}(n+1)}}\in \mathbb {Q} ^{+}

Les premières images de cette fonction sont :

0,1,{\frac {1}{2}},2,{\frac {1}{3}},{\frac {3}{2}},{\frac {2}{3}},3,{\frac {1}{4}},{\frac {4}{3}},{\frac {3}{5}},\dots

Le nombre fusc(n) / fusc(n + 1) est en effet le n-ième nombre rationnel du parcours en largeur de l'arbre de Calkin-Wilf, qui établit une telle bijection.

La suite de Stern apparaît aussi dans les numérateurs et dénominateurs des fractions construites au moyen de l'arbre de Stern-Brocot, et qui établit également une bijection entre les entiers positifs ou nuls et les rationnels positifs ou nuls.

Suite de Stern et fonction ?( ) de Minkowski

Considérons la fonction f suivante, définie sur les nombres dyadiques :

f\left({\frac {k}{2^{n}}}\right)={\frac {{\rm {fusc}}(k)}{{\rm {fusc}}(2^{n}+k)}},k\leq 2^{n}

Cette fonction se prolonge sur [0,1] en une fonction continue strictement croissante, bijective de [0,1] sur [0,1], appelée fonction boîte de Conway. La réciproque de cette extension est la fonction point d'interrogation de Minkowski.

Voir aussi

Bibliographie

La suite de Stern-Brocot, sœur de Fibonacci, dans Pour la Science, n° 420, oct. 2012
Sam Northshield, Stern's diatomic sequence, American Math. Monthly, 117, (août-septembre 2010), 581-598

Articles connexes

Références

↑ M. A. Stern, Über einse zahlentheoretische Function, J. Reine Agnew. Math., 55, (1858), 193-220
↑ (en) E. W. Dijkstra, « An exercise for Dr.R.M.Burstall », 1976
↑ (en) E. W. Dijkstra, « More about the function “fusc” (A sequel to EWD570) », 1976
↑ Valerio De Angelis, « The Stern Diatomic Sequence via the Generalised Chebyshev Polynomials », Amer. Math. monthly, vol. 124, n^o 5,‎ mai 2017, p. 451-455. La démonstration consiste à vérifier que le déterminant et la suite de Stern vérifie des relations de récurrence identiques.
↑ Richard P. Stanley, « Some Linear Recurrences Motivated by Stern's Diatomic Array », Amer. Math. Monthly, vol. 127, n^o 2,‎ février 2020, p. 100
↑ S. R. Finch, Mathematical constants, Encyclopedia of mathematics and its applications, vol.94 Cambridge University Press, (2003)
↑ L. Carlitz, A problem in partitions related to the Stirling numbers, Bull. Amer. Math. Soc., 70, (1964), 275-278
↑ Neil Calkin, Herbert S. Wilf, « Recounting the Rationals », Amer. Math. Monthly, avril 2000, p. 360-363

Portail des mathématiques

[1] M. A. Stern, Über einse zahlentheoretische Function, J. Reine Agnew. Math., 55, (1858), 193-220

[2] (en) E. W. Dijkstra, « An exercise for Dr.R.M.Burstall », 1976

[3] (en) E. W. Dijkstra, « More about the function “fusc” (A sequel to EWD570) », 1976

[4] Valerio De Angelis, « The Stern Diatomic Sequence via the Generalised Chebyshev Polynomials », Amer. Math. monthly, vol. 124, n^o 5,‎ mai 2017, p. 451-455. La démonstration consiste à vérifier que le déterminant et la suite de Stern vérifie des relations de récurrence identiques.

[5] Richard P. Stanley, « Some Linear Recurrences Motivated by Stern's Diatomic Array », Amer. Math. Monthly, vol. 127, n^o 2,‎ février 2020, p. 100

[6] S. R. Finch, Mathematical constants, Encyclopedia of mathematics and its applications, vol.94 Cambridge University Press, (2003)

[7] L. Carlitz, A problem in partitions related to the Stirling numbers, Bull. Amer. Math. Soc., 70, (1964), 275-278

[8] Neil Calkin, Herbert S. Wilf, « Recounting the Rationals », Amer. Math. Monthly, avril 2000, p. 360-363

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]