Moiré (physique)

Le moiré[1] est un effet de contraste changeant avec la déformation d'un objet, indépendamment des effets d'ombre. On parle souvent du moiré d'une étoffe (par exemple de la soie). On peut obtenir un effet similaire en superposant deux voiles à maille régulière, ou bien lorsque l'on observe deux grillages l'un derrière l'autre, ou encore deux rambardes de pont, à une certaine distance.
D'une manière générale, le moiré est une figure composée de lignes sombres et claires résultant de la superposition de deux réseaux (ensemble de lignes globalement parallèles). Il s'agit en fait d'un phénomène d'interférences spatiales entre les deux réseaux. Ce phénomène peut être utilisé pour analyser la déformation d'un objet ; il permet aussi d'expliquer le phénomène de tramage que l'on a lorsque l'on numérise (« scanne ») une image composée de points (comme une photo de quotidien), ou bien l'effet étrange produit par une chemise à rayures à la télévision (superposition de la trame de la chemise et de la trame de l'écran).
Réseaux parallèles de pas différent[modifier | modifier le code]
Approche géométrique[modifier | modifier le code]

Considérons deux réseaux constitués de lignes parallèles équidistantes, par exemple verticales. Le premier réseau a un pas p, le second a un pas p + δp, avec δp > 0.
Si nous faisons coïncider les traits les plus à gauche des réseaux, le décalage entre les traits des deux réseaux s'accentue lorsque l'on va vers la droite. Au bout d'un certain nombre de traits, les deux réseaux seront en opposition : les traits du deuxième réseau seront entre les traits du premier réseau. De loin, on va donc avoir une impression de clair lorsque les traits des deux réseaux sont superposés (il y a du blanc entre les traits), et une impression de sombre lorsque les traits sont en opposition.
La première ligne sombre apparaît lorsque le décalage est p/2. Le trait n du second réseau est décalé de n·δp par rapport au trait n du premier réseau. La première ligne sombre apparaît donc pour
- .
soit
- .
La distance d séparant une ligne sombre d'une ligne claire est donc
la distance séparant deux lignes sombres, qui est également la distance séparant deux lignes claires, est
On déduit de cette formule que :
- plus le pas est grand, plus les lignes claires et sombres sont espacées ;
- plus l'écart de pas δp est grand, plus les lignes claires et sombres sont rapprochées. Lorsque δp tend vers l'infini, l'écart entre les lignes tend vers p : on retrouve le pas du premier réseau.
- à l'inverse, des lignes très espacées signifient que les réseaux ont des pas très proches. Lorsque δp tend vers 0, l'écart entre les lignes tend vers l'infini : on obtient une figure uniforme, sans variation de contraste.
Le principe du moiré est similaire à celui du vernier.
Approche sinusoïdale[modifier | modifier le code]

Si l'on ne considère plus des réseaux de lignes de fort contraste, mais des réseaux transparents ayant un contraste I variant de manière continue selon une sinusoïde
(les pas sont respectivement de p1 = 1/k1 et p2 = 1/k2), l'intensité lorsque l'on superpose les deux réseaux est alors
soit, d'après la formule de la somme de deux sinus dérivée des formules d'Euler :

On voit donc que l'intensité résultante est composée d'une sinusoïde ayant une « fréquence spatiale » (nombre d'onde) élevée qui est la moyenne des fréquences spatiales des deux réseaux, et d'une sinusoïde ayant une fréquence spatiale faible qui est la moitié de la différence des fréquences spatiales des deux réseaux. Cette deuxième composante est une « enveloppe » pour l'autre sinusoïde. La longueur d'onde λ de cette composante est l'inverse de la fréquence spatiale
soit si l'on pose p1 = p et p2 = p+δp :
- .
Les zéros de cette enveloppe sont espacés de λ/2, et les maxima d'amplitude en valeur absolue sont espacés également de λ/2 ; on retrouve donc le résultat de l'approche classique.
Ce phénomène est semblable à la stroboscopie temporelle, ou à la production de battements sonores.
Réseaux non parallèles de même pas[modifier | modifier le code]

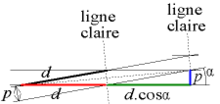
Considérons deux réseaux de même pas p, mais désorientés d'un angle α. De loin, on voit également apparaître des lignes sombres et claires : les lignes claires correspondent aux lignes des nœuds, c'est-à-dire aux lignes passant par les points d'intersection des deux réseaux.
Si l'on considère une « maille du filet », on voit que cette maille est un losange : c'est un parallélogramme dont les côtés valent d = p/sin α (on a un triangle rectangle d'hypoténuse d et dont le côté opposé à l'angle α vaut p).
Les lignes claires correspondent à la petite diagonale du losange. Comme les diagonales sont les bissectrices des côtés adjacents, on en déduit que la ligne claire fait un angle α/2 par rapport à la perpendiculaire de chacun des réseaux.
Par ailleurs, l'espacement entre deux lignes claires est égal à la grande diagonale (c'est également la distance séparant deux lignes sombres). Cette grande diagonale D est l'hypoténuse d'un triangle rectangle dont les côtés de l'angle droit valent d(1+cos α) et p. D'après le théorème de Pythagore, on a :
soit

Si α est très petit (α << 2π), on peut faire les approximations suivantes :
- sin α ≈ α
- cos α ≈ 1
soit
- D ≈ p / α
α étant exprimé en radians On voit que plus α est faible, plus les lignes sont écartés ; lorsque les deux réseaux sont parallèles (α = 0), l'écart des lignes est « infini » (il n'y a pas de ligne).
On a donc deux manières de déterminer α : par l'orientation des lignes claires et par leur espacement
- α ≈ p /D
Si l'on choisit de mesurer l'angle, on a une erreur finale proportionnelle à l'erreur de mesure de l'angle. Si l'on choisit de mesurer la distance, on a une erreur finale inversement proportionnelle à l'erreur de distance. Donc, pour les petits angles, il vaut mieux se fier à la mesure de distance.
Application à l'extensométrie[modifier | modifier le code]

Le moiré peut être utilisé en extensométrie : il suffit de tracer un réseau sur la pièce à étudier, et de superposer le réseau de référence au réseau déformé par la déformation de la pièce.
On peut également superposer une image holographique de l'objet à l'objet lui-même ; les écarts entre l'image (la référence) et l'objet sont dues à des déformations de l'objet, et ces écarts génèrent des franges claires et sombres.
Voir aussi :
Traction uniaxiale[modifier | modifier le code]
Considérons une pièce de longueur l sur laquelle on trace un réseau de pas p dont les traits sont perpendiculaires à l'axe de traction.
Sous tension, la pièce a une longueur l·(1+ε), où ε est la déformation (allongement relatif). Le pas du réseau devient p·(1+ε), on a donc δp = p·ε.
On voit que l'espacement entre deux zones sombre vaut :
donc cet espacement permet de déterminer la déformation. Toutefois, la mesure de la distance entre deux sombres est imprécise, du fait de la largeur d'une zone. On peut se contenter de compter le nombre N de traits sombres que l'on voit : sur une longueur l, on a
soit
La précision est la déformation qui sépare deux apparitions de traits, soit
Cisaillement[modifier | modifier le code]
Dans le cas du cisaillement pur, il suffit de tracer un réseau perpendiculaire aux forces de scission. Le réseau sur la pièce déformée est alors tourné de l'angle de cisaillement γ par rapport au réseau de référence (pièce non déformée).
De même que pour la traction uniaxiale, on peut se contenter de compter le nombre de traits, à condition que γ soit très faible, que la pièce soit rectangulaire, et que les forces soient parallèles aux côtés (les lignes claires sont alors quasiment parallèles aux côtés de la pièce).
Si la largeur de la pièce (perpendiculairement aux forces) est l, alors le nombre de traits N vaut :
soit
avec comme ci-dessus une erreur
Mesure de petits déplacements[modifier | modifier le code]

Considérons un réseau fixé sur une pièce, observé au travers d'un réseau de pas légèrement différent, considéré comme fixe. On a donc un moiré.
Lorsque la pièce se déplace, les traits sombres et clairs du moiré se déplacent aussi :
- pour un déplacement de δp, les traits se déplacent de p, dans le sens inverse du mouvement.
On retrouve le comportement du vernier. On a donc un facteur d'amplification de p/δp. Cela permet de mesurer de petits mouvements, ainsi que des faibles vitesses.
Imprimerie[modifier | modifier le code]
Le phénomène de moirage apparaît aussi en imprimerie par le fait que les quatre couches composant une image quadrichromique sont faites d'un maillage appelé trame dont l'inclinaison est différente pour chaque couleur (0, 15, 45 et 75° par exemple). Dans certaines situations, il arrive que la superposition de deux trames provoque un moiré. On y remédie en augmentant ou diminuant la fréquence de la trame électronique.
Moirage numérique[modifier | modifier le code]


Dans la chaîne de traitement numérique d'une image, un moirage peut apparaître soit à l'étape de la numérisation soit à celle de l'affichage.
Dans le premier cas, elle résulte d'une interférence entre la trame du capteur (scanner ou matrice) et celle de l'objet numérisé. Dans le cas de capteurs couleurs, elle peut également générer des effets colorés dans une image qui en est normalement dépourvue.
Dans le second cas, le moirage résulte de l'interférence entre la matrice de pixels de l'écran et la trame de l'objet affiché. Ce problème est similaire aux effets analogiques d'impression par tramage décrits précédemment.
Démoirage[modifier | modifier le code]


Il est possible de diminuer les effets du moiré en appliquant des filtres ou avec quelques astuces. Dans le cas d'une numérisation d'un document, on peut limiter le moiré en tournant l'image. L'échantillonnage ne se faisant plus sur les mêmes axes, l'effet peut être réduit ou amplifié. Le filtrage avec un flou gaussien limite le moiré sans toutefois complètement l'éradiquer. Des résultats similaires sont obtenus avec un filtre médian.
Bien souvent, les pilotes des scanneurs sont fournis avec une option pour enlever le moiré. Les algorithmes peuvent être plus ou moins évolués mais en général, la méthode habituelle consiste à agrandir fortement l'image via une interpolation et à appliquer un flou gaussien sur cette version suréchantillonnée. On peut ensuite diminuer la taille de l'image de manière que les dimensions correspondent à l'original. Un filtre de type « accentuation » peut être appliqué pour relever les détails.
Les filtrages plus avancés profitent du fait que le moiré a une certaine fréquence avec en général une prédominance dans un axe particulier. Avec des filtres passe-bande, il est possible d'éliminer du spectre les fréquences liées au moiré. Toutefois, ce problème reste difficile en pratique car le phénomène est souvent non-linéaire (images provenant d'un système analogique) ou perturbé par du bruit.
Annexes[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
Notes et références[modifier | modifier le code]
- de l'arabe مخير mukháyyar, « choisi », qui a donné mohair




















