Forme cristalline

Une forme cristalline est un ensemble de faces d'un cristal qui sont dans un rapport de symétrie, c'est-à-dire qui sont équivalentes entre elles par l'application d'opérations d'un groupe ponctuel de symétrie. Une forme est indiquée par les indices de Miller (hkl) d'une de ses faces, de préférence celle qui a les valeurs les plus positives. Les indices d'une forme sont écrits entre accolades : {hkl}.

Une forme cristalline est caractérisée par :

la multiplicité qui est le nombre des faces ; elle dépend de la symétrie du cristal et de l'orientation de la face originale par rapport aux éléments de symétrie du cristal ;
sa symétrie propre ;
son nom officiel^[1].

Il existe plusieurs critères de classification des 47 formes cristallines, qui peuvent être ouvertes ou fermées :

formes caractéristiques et non-caractéristiques ;
formes générales et particulières ;
formes basiques et limites.

Les formes cristallines permettent de décrire l'habitus d'un cristal.

Classification des formes cristallines[modifier | modifier le code]

Formes caractéristiques et non-caractéristiques[modifier | modifier le code]

Ce critère intègre la possibilité de cristaux de symétries différentes de développer la même forme.

Notons G le groupe ponctuel qui correspond à la symétrie propre de la forme et H le groupe ponctuel du cristal qui a développé cette forme : soit H coïncide avec G lui-même ; soit avec un de ses sous-groupes, ce qu'on écrit H $\subseteq$ G.

Lorsque H = G, on parle de « forme caractéristique », tandis que H $\subseteq$ G correspond à une « forme non-caractéristique ». Dans les systèmes cristallins triclinique et monoclinique, toute forme est non-caractéristique.

La forme cristalline d'un cristal est donc caractéristique si son groupe ponctuel de symétrie propre est identique au groupe ponctuel de symétrie du cristal.

Exemple

La symétrie propre du prisme ditétragonal est 4/mmm : il se présente comme une forme {hk0} dans les groupes ponctuels 4/mmm, 42m, 4mm et 422. C'est donc seulement dans le premier cas qu'il s'agit d'une forme caractéristique.

Formes générales et particulières[modifier | modifier le code]

Lorsque les pôles des faces d'une forme cristalline se trouvent sur des éléments de symétrie (axes ou miroirs), la forme est dite « particulière », sinon elle est « générale ».

Exemple

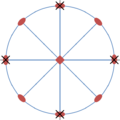
Le prisme tétragonal se présente comme forme {100} dans tous les groupes ponctuels tétragonaux. Toutefois, il s'agit d'une forme particulière dans les groupes 4/mmm, 42m, 4mm, 422 et 4/m, mais d'une forme générale dans les groupes 4 et 4. Sa symétrie propre étant 4/mmm, elle est caractéristique dans le groupe 4/mmm et non-caractéristique dans tous les autres groupes. Dans les figures ci-dessous sont montrées les projections stéréographiques du prisme tétragonal dans les groupes ponctuels tétragonaux. Les plans miroirs sont représentés en bleu, les axes de rotation en rouge^[2] et les pôles des faces par les croix noires.

Groupe 4/mmm
Groupe 4/m
Groupe 4mm
Groupe 42m
Groupe 422
Groupe 4
Groupe 4

Formes basiques et limites[modifier | modifier le code]

Lorsqu'une forme peut être obtenue comme limite d'une autre forme ayant la même multiplicité (nombre de faces) et la même orientation mais une symétrie propre supérieure, cette forme s'appelle « forme limite » et celle à partir de laquelle cette forme a été obtenue s'appelle « forme basique ».

Exemple

Dans le groupe ponctuel 4mm, la pyramide tétragonale et le prisme tétragonal ont la multiplicité 4 et peuvent être orientés soit selon les axes cristallographiques a et b, soit selon les bissectrices des axes. La pyramide, forme basique, a la symétrie propre 4mm tandis que le prisme, forme limite, a la symétrie propre 4/mmm. Le prisme peut être imaginé comme le résultat de l'ouverture de la pyramide à son sommet et du changement de la pente des faces, jusqu'à la limite où celles-ci deviennent parallèles, formant ainsi un prisme.

Les 47 formes cristallines[modifier | modifier le code]

On distingue deux sortes de forme cristalline :

les « formes ouvertes » dont les faces ne forment pas rigoureusement un volume ; une ou plusieurs faces du volume n'appartenant pas à la forme cristalline. Dans les représentations graphiques, on reconnaît ces formes à l'absence d'une ou plusieurs faces ; absence qui peut être figurée par exemple à l'aide de polygones hachés comme ci-dessous ;
les « formes fermées » qui sont des volumes, aucune face ne manquant.

Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée.

Exemple

La forme {111} comprend la face (111) et toutes les faces équivalentes à (111) par symétrie.

Si le groupe ponctuel du cristal est 1, la forme {111} a multiplicité 2 et est composée de deux plans parallèles, (111) et (1 $\,$ 1 $\,$ 1) : cette forme s'appelle « pinacoïde ».
Si le groupe ponctuel du cristal est 3, la forme {111} a multiplicité 8 et est composée de huit faces qui sont des triangles équilatères : (111), (111), (111), (111), (11 $\,$ 1), (111), (1 $\,$ 11) et (1 $\,$ 1 $\,$ 1). Cette forme est un octaèdre.

	Nom	Symétrie propre	Multiplicité	Description	Représentation
1	Pédion	$\infty$ m	1	Dite aussi monoèdre, cette forme ouverte est composée d'un seul plan.
2	pinacoïde	$\infty$ m/m	2	Forme ouverte composée de deux plans parallèles.
3	Dièdre	mm2	2	Forme ouverte composée de deux plans qui se coupent en une arête commune^[3].
4	prisme rhombique	mmm	4	Forme ouverte composée de quatre plans non parallèles.
5	Pyramide rhombique	mm2	4	Forme ouverte composée de quatre triangles scalènes.
6	Pyramide trigonale	3m	3	Forme ouverte composée de trois triangles isocèles.
7	Pyramide tétragonale	4mm	4	Forme ouverte composée de quatre triangles isocèles.
8	Pyramide hexagonale	6mm	6	Forme ouverte composée de six triangles isocèles.
9	Pyramide ditrigonale	3m	6	Forme ouverte composée de six triangles isocèles.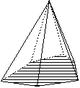
10	Pyramide ditétragonale	4mm	8	Forme ouverte composée de huit triangles isocèles.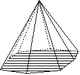
11	Pyramide dihexagonale	6mm	12	Forme ouverte composée de douze triangles isocèles.
12	Prisme trigonal	62m	3	Forme ouverte composée de trois plans non parallèles.
13	Prisme tétragonal	4/mmm	4	Forme ouverte composée de quatre plans non parallèles.
14	Prisme hexagonal	6/mmm	6	Forme ouverte composée de six plans non parallèles.
15	Prisme ditrigonal	62m	6	Forme ouverte composée de six plans non parallèles.
16	Prisme ditétragonal	4/mmm	8	Forme ouverte composée de huit plans non parallèles.
17	Prisme dihexagonal	6/mmm	12	Forme ouverte composée de douze plans non parallèles.
18	Disphénoïde rhombique	222	4	Forme fermée composée de quatre triangles scalènes. Parfois appelée improprement « tétraèdre rhombique » (le tétraèdre est une forme cubique).
19	Bipyramide rhombique	mmm	8	Forme fermée composée de huit triangles scalènes.
20	Bipyramide trigonale	62m	6	Forme fermée composée de six triangles isocèles.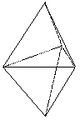
21	Bipyramide tétragonale	4/mmm	8	Forme fermée composée de huit triangles isocèles.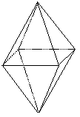
22	Bipyramide hexagonale	6/mmm	12	Forme fermée composée de douze triangles isocèles.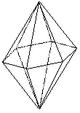
23	Bipyramide ditrigonale	62m	12	Forme fermée composée de douze triangles isocèles.
24	Bipyramide ditétragonale	4/mmm	16	Forme fermée composée de seize triangles isocèles.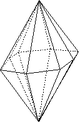
25	Bipyramide dihexagonale	6/mmm	24	Forme fermée composée de vingt-quatre triangles isocèles.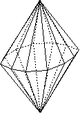
26	Disphénoïde tétragonal	42m	4	Forme fermée composée de quatre triangles isocèles. Parfois appelée improprement « tétraèdre tétragonal » (le tétraèdre est une forme cubique).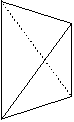
27	Rhomboèdre	3m	6	Forme fermée composée de six losanges. Cette forme peut présenter sous deux orientations différant de 180º autour de l'axe ternaire : on parle alors de rhomboèdre direct et rhomboèdre inverse.
28	Scalénoèdre tétragonal	42m	8	Forme fermée composée de huit triangles scalènes.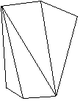
29	Scalénoèdre ditrigonal	3m	12	Forme fermée composée de douze triangles scalènes. Si les angles dièdres entre paires de faces sont tous égaux, on parle de scalénoèdre hexagonal.
30	Trapézoèdre tétragonal	422	8	Forme fermée composée de huit trapèzes.
31	Trapézoèdre trigonal	32	6	Forme fermée composée de six trapèzes.
32	Trapézoèdre hexagonal	622	12	Forme fermée composée de douze trapèzes.
33	Tétartoïde ou pentagono- tritétraèdre	23	12	Forme fermée composée de douze pentagones.
34	Pentagono- dodécaèdre	m3	12	Dite aussi dihexaèdre ou pyritoèdre, cette forme fermée est composée de douze pentagones.
35	Diploèdre ou didodécaèdre	m3	24	Forme fermée composée de vingt-quatre trapèzes.
36	Gyroïde ou pentagono- trioctaèdre	432	24	Forme fermée composée de vingt-quatre pentagones.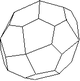
37	Tétraèdre	43m	4	Forme fermée composée de quatre triangles équilatères.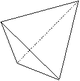
38	Tétragono- tritétraèdre	43m	12	Dite aussi deltoèdre ou trapézododécaèdre, cette forme fermée est composée de douze trapèzes.
39	Trigono- tritétraèdre	43m	12	Forme fermée composée de douze triangles isocèles.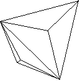
40	Hexatétraèdre	43m	24	Forme fermée composée de vingt-quatre triangles scalènes.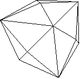
41	Cube ou hexaèdre	m3m	6	Forme fermée composée de six carrés.
42	Octaèdre	m3m	8	Forme fermée composée de huit triangles équilatères.
43	Rhombo- dodécaèdre	m3m	12	Forme fermée composée de douze losanges.
44	Trigono- trioctaèdre	m3m	24	Forme fermée composée de vingt-quatre triangles isocèles.
45	Tétragono- trioctaèdre	m3m	24	Dite aussi icositétraèdre ou leucitoèdre, cette forme fermée est composée de vingt-quatre trapèzes.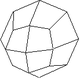
46	Tétrahexaèdre	m3m	24	Forme fermée composée de vingt-quatre triangles isocèles.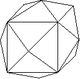
47	Hexaoctaèdre	m3m	48	Forme fermée composée de quarante-huit triangles scalènes.

Forme cristalline et habitus[modifier | modifier le code]

Les formes cristallines sont utilisées pour décrire l'habitus d'un cristal.

Par exemple, dans la figure ci-contre, l'habitus de la calcite (de groupe d'espace R3m) est constitué d'un prisme hexagonal {1010} terminé par les faces du rhomboèdre {1011}.

Notes et références[modifier | modifier le code]

↑ J.D.H. Donnay et H. Curien, « Nomenclature des 47 formes cristallines », Bulletin de la Société française de Minéralogie et Cristallographie, vol. 81,‎ 1958, p. XLIV-XLVII
↑ Les éléments de symétrie sont représentés par des symboles définis dans les International Tables for Crystallography, vol. A: Space-group symmetry, Kluwer Academic Publishers, 2005, 938 p. (ISBN 978-0-7923-6590-7), chap. 1.4 (« Graphical symbols for symmetry elements in one, two and three dimensions »), p. 9 (en)
↑ Si on considère les propriétés physiques, les deux plans du dièdre peuvent être reliés par un axe binaire ou par un miroir, ce qui réduit la symétrie propre de la forme de mm2 à 2 ou m respectivement. Le dièdre prend alors respectivement le nom de sphénoïde ou de dome. Cette distinction, opérée par certains textes, a été critiquée à plusieurs reprises, car elle n'est appliquée qu'au dièdre. La même distinction appliquée à toutes les formes emmène celles-ci au nombre de 130. (M. Nespolo, « The ash heap of crystallography: restoring forgotten basic knowledge », Journal of Applied Crystallography, vol. 48,‎ 2015, p. 1290-1298 (lire en ligne))

Bibliographie[modifier | modifier le code]

(en) International Tables for Crystallography, vol. A : Space-group symmetry, M. Aroyo, Wiley, 2016, 6^e éd. (ISBN 978-0-470-68575-4, lire en ligne), partie 3, chap. 2, p. 1.2

[1] J.D.H. Donnay et H. Curien, « Nomenclature des 47 formes cristallines », Bulletin de la Société française de Minéralogie et Cristallographie, vol. 81,‎ 1958, p. XLIV-XLVII

[2] Les éléments de symétrie sont représentés par des symboles définis dans les International Tables for Crystallography, vol. A: Space-group symmetry, Kluwer Academic Publishers, 2005, 938 p. (ISBN 978-0-7923-6590-7), chap. 1.4 (« Graphical symbols for symmetry elements in one, two and three dimensions »), p. 9 (en)

[3] Si on considère les propriétés physiques, les deux plans du dièdre peuvent être reliés par un axe binaire ou par un miroir, ce qui réduit la symétrie propre de la forme de mm2 à 2 ou m respectivement. Le dièdre prend alors respectivement le nom de sphénoïde ou de dome. Cette distinction, opérée par certains textes, a été critiquée à plusieurs reprises, car elle n'est appliquée qu'au dièdre. La même distinction appliquée à toutes les formes emmène celles-ci au nombre de 130. (M. Nespolo, « The ash heap of crystallography: restoring forgotten basic knowledge », Journal of Applied Crystallography, vol. 48,‎ 2015, p. 1290-1298 (lire en ligne))

[1]

[2]

[3]