Fonction NON-ET
| Entrées | Sortie | |
| a | b | L |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

La fonction ET-NON (NAND en anglais) est un opérateur logique de l'algèbre de Boole. À deux opérandes, qui peuvent avoir chacun la valeur VRAI ou FAUX, il associe un résultat qui a lui-même la valeur VRAI seulement si au moins l'un des deux opérandes a la valeur FAUX.
Les notations usuelles sont ou ou
Équation[modifier | modifier le code]
Ce qui peut se lire : « NON( A ET B ) est équivalent à : NON( A ) OU NON( B ) »
Illustration[modifier | modifier le code]
Une lampe s'allume sauf si l'on appuie sur « a » et « b » et seulement dans ce cas-là. La fonction « ET-NON » est caractérisée par des contacts NF (normalement fermés) montés en parallèle.
-
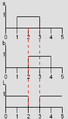
Chronogramme de la fonction NON-ET.
Symbole[modifier | modifier le code]
Symbole ANSI[modifier | modifier le code]
Universalité de la fonction ET-NON[modifier | modifier le code]
La fonction ET-NON est dite « universelle » (comme la fonction OU-NON), car elle permet de reconstituer toutes les autres fonctions logiques. De plus, son circuit électronique en CMOS étant des plus simples, la fonction ET-NON sert souvent de « brique de base » à des circuits intégrés beaucoup plus complexes.
Fonction Non[modifier | modifier le code]
Fonction ET[modifier | modifier le code]
Fonction OU[modifier | modifier le code]
| Schéma | Table de vérité | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

|
| ||||||||||||||||||||||||||||||
Fonction OU exclusif[modifier | modifier le code]
Implémentations[modifier | modifier le code]
Un processeur peut être entièrement réalisé en utilisant uniquement des fonctions ET-NON. Pour les circuits intégrés TTL utilisant des transistors à plusieurs émetteurs, utiliser des fonctions ET-NON nécessite moins de transistors qu'avec des fonctions NON-OU.
Schémas[modifier | modifier le code]
 |
 |
 |
 |
Exemples de dispositions physiques[modifier | modifier le code]
 |
 |
Circuit intégré 7400[modifier | modifier le code]
Différents circuits intégrés de la série 7400 intègrent des portes logiques ET-NON, en nombre et caractéristiques analogiques variables : 7400, 7401, 7402, 7403, 7410, 7412, 7413, 7420, 7422, 7424, 7426, 7430, 7437, 7438, 7439, 7440, 74618, 74800, 74804.