Barre de torsion

La barre de torsion est un des types de ressort les plus simples. En mettant à profit l'élasticité transverse des matériaux, il autorise de grandes déformations de structures, et permet la construction d'éléments d'une souplesse plus facile à contrôler.
Il ne faut pas confondre ce phénomène avec celui des ressorts de torsion en spirale utilisés en horlogerie, qui eux travaillent en réalité en flexion.
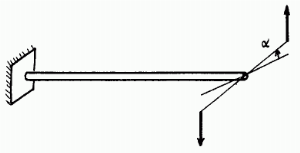
Pour la barre de torsion, si nous négligeons les extrémités, sa partie active est une barre pleine de diamètre d et de longueur L, ou bien un tube de diamètre intérieur di et de diamètre extérieur de.
L'une des extrémités de la barre est bloquée et considérée comme fixe, l'autre, dite libre, est reliée aux éléments mobiles.
L'application essentielle des barres de torsion est la suspension des véhicules, particulièrement de ceux dont les roues sont indépendantes. On les utilise non seulement sur des véhicules légers, mais aussi sur des engins de masse importante (char d'assaut par exemple) et beaucoup de véhicules tout-terrain.
Appelons Mt le moment de torsion appliqué à l'extrémité libre de la barre et α l'angle dont tourne cette extrémité par rapport à l'autre, sous l'effet de ce moment.
Condition de résistance[modifier | modifier le code]
La contrainte maximale de cisaillement dans le ressort vaut :
avec (barre pleine)
ou (tube)
Condition de déformation[modifier | modifier le code]
L'angle de rotation de l'extrémité libre vaut :
avec (barre pleine)
ou (tube)
La raideur vaut
Les inconnues sont faciles à obtenir à partir des formules : en effet, pour un matériau donné, les diamètres de la barre ou du tube sont fixés par la condition de résistance, ensuite la condition de déformation impose la longueur.
Avec :
G : Le module de cisaillement
: Le moment quadratique dans l'axe de la barre
: L'angle de rotation de l'extrémité libre
L: La longueur de la barre
Mt : Le moment
k : La raideur
d : Le diamètre
Problèmes pratiques[modifier | modifier le code]
Dans les barres de torsion à section circulaire, le problème délicat est celui des attaches, au niveau desquelles il ne faut pas provoquer de concentration de contrainte. Le plus souvent, un cône de demi angle au sommet proche de 30°, raccordé à la barre par un large congé de raccordement (rayon r ~ 1,5.d), permet l'augmentation de diamètre nécessaire à la réalisation des cannelures qui seront engagées dans les parties femelles des pièces de liaison. La concentration de contrainte due au changement de rayon sera faible, en revanche les cannelures assurant la transmission de couple donneront un coefficient de concentration de contrainte voisin de 2.

Il est possible d'associer une barre et un tube de torsion afin de diminuer l'encombrement en longueur (suspension dite « Dubonnet »). Un ressort de torsion fait d'un tube aura un état de contrainte tendant vers un champ uniforme, donc sera de volume minimal. En revanche, un calcul élémentaire donne le cylindre de révolution de longueur minimale.

Applications dans le domaine des transports[modifier | modifier le code]
Suspensions[modifier | modifier le code]
L'utilisation des barres de torsion à la place de ressorts plus traditionnels apporte bon nombre d'avantages pour la suspension des automobiles, camionnettes et remorques : la compacité, la souplesse, un grand débattement et un faible encombrement.
On peut ainsi citer les trains avant et arrière du fourgon Citroën Type H ou des premières versions de la Coccinelle VW (jusqu'en 1970) avec des barres longitudinales, ainsi que bon nombre de voitures Panhard d'après-guerre. Renault a aussi abondamment utilisé le système des barres de torsion : barres longitudinales (sur le train avant) et barres transversales (sur le train arrière) de la Renault 4 où la précontrainte est d'ailleurs réglable en atelier, ce qui permet de surélever la voiture pour circuler sur de mauvais chemins même avec de fortes charges.
Du fait de la juxtaposition des barres de torsion sous la voiture, l'empattement du véhicule est différent entre la gauche et la droite de la voiture. Renault a repris ce système sur beaucoup de ses véhicules à traction avant comme la Renault 6, la Renault 16, le break Renault 21 Nevada (avec un ressort secondaire classique sur l'amortisseur).
Le fabricant français d'essieux de remorques "Frankel" commercialisait d'excellents essieux à barres de torsion pour les fabricants de remorques et de caravanes, mais cette solution mécaniquement noble et coûteuse a été abandonnée lors de l'absorption de la firme par le groupe allemand Al-Ko, au profit d'un système de tubes emboîtés avec interposition de cordes de caoutchouc.
La suspension par barres de torsion a également été utilisée sur nombre de chars de combat et autres engins militaires blindés.
Distribution[modifier | modifier le code]
Beaucoup plus marginale est l'utilisation des barres de torsion pour le rappel des soupapes dans la distribution des moteurs automobiles et motocyclistes:
Solution efficace évitant certains problèmes liés aux ressorts à boudin à l'époque où leur métallurgie n'était pas maîtrisée totalement (affolement des soupapes, bris du fil de ressort, phénomènes de résonance), c'est néanmoins une solution d'une certaine complexité qui nécessite de la place dans la culasse. Elle a été employée pour des moteurs à haut rendement (pour l'époque) et conçus pour les hauts régimes de rotation.
Les deux exemples les plus connus sont le moteur "Flat Twin" des Panhard Dyna,PL17, 24 et CD et, dans le domaine motocycliste le très performant bicylindre vertical de la Honda CB 450 des années 70 qui surclassait les motos anglaises de la même époque disposant d'une cylindrée largement supérieure.









