Combinatoire des mots

Construction de la suite de Prouhet-Thue-Morse.

La combinatoire des mots est une branche des mathématiques et de l'informatique théorique qui applique l'analyse combinatoire aux mots finis ou infinis. Cette branche s'est développée à partir de plusieurs branches des mathématiques : la théorie des nombres, la théorie des groupes, les probabilités et bien sûr la combinatoire. Elle a des liens avec divers thèmes informatiques, comme l'algorithmique du texte, la recherche de motifs et la compression de textes.

Champs d'étude et applications

La combinatoire des mots a pour objet d'étude les propriétés de mots finis ou mots infinis particuliers. Ceci est à comparer à la théorie des langages formels, qui s'intéresse aux ensembles de mots, en vue de leur représentation et leur analyse.

Pour une classe de mots, l'étude porte sur les caractérisations équivalentes, les propriétés combinatoires, le dénombrement, l'énumération systématique ou la génération aléatoire. On étudie aussi les algorithmes et leur efficacité pour la réalisation effective de ces opérations.

La combinatoire des mots a des applications dans des domaines variés de l'informatique théorique, comme la théorie des automates et de la linguistique. Le développement du texte numérique et du traitement de texte a amené à d'importants développements de la combinatoire des mots. Elle est présente à la base de l'algorithmique du texte, du traitement automatique du langage naturel, du traitement de la parole et du bio-informatique.

Historique

La combinatoire des mots remonte aux travaux d'Axel Thue sur les suites non-répétitives de symboles, au début du XX^e siècle. Les principaux travaux, dans les années qui ont suivi, sont ceux de Marston Morse et de ses coauteurs sur la suite de Prouhet-Thue-Morse et les mots sturmiens. Une célèbre application de la combinatoire des mots est l'usage qui est fait d'une suite sans répétition dans la réponse négative à la conjecture de Burnside apportée par Piotr Novikov et Adian.

C'est Marcel-Paul Schützenberger qui est le fondateur de la combinatoire des mots moderne, notamment dans des travaux avec Roger C. Lyndon et André Lentin. Ses cours ont été rédigés par Jean-François Perrot, et ont donné naissance au livre « Combinatorics on words », ouvrage collectif signé du nom de plume M. Lothaire, et paru en 1983. La combinatoire des mots se développa rapidement à partir de cette date. Deux autres livres de synthèse, signés Lothaire, paraissent ultérieurement, et plusieurs ouvrages collectifs prennent leurs suite.

Thèmes

Mots de Lyndon

Les mots de Lyndon, nommés ainsi d'après le mathématicien Roger Lyndon, sont les mots primitifs et minimaux dans leur classe de conjugaison. L'un des résultats de base est que tout mot admet une factorisation décroissante unique en mots de Lyndon (résultat attribué par erreur à Chen, Fox et Lyndon). Un autre résultat remarquable est que le produit, en ordre croissant, des mots de Lyndon dont la longueur divise un entier donné est un mot de de Bruijn.

Répétitions

La combinatoire des mots s'est notamment attachée à décrire les conditions dans lesquelles les répétitions apparaissent dans les mots (mots sans carré, entre autres), la construction ou la transformation des mots, par morphisme. Un cas plus général est couvert par la notion de motif inévitable ou son contraire, les motifs évitables. Par exemple le « motif » $xyxyx$ (où $x$ et $y$ sont des symboles) dénote la présence, dans un mot, d'un facteur de la forme $uvuvu$ (où cette fois-ci, $u$ et $v$ sont des mots). Dire qu'un mot évite ce motif, c'est qu'il ne contient pas ce facteur. Dire qu'un motif est inévitable, c'est affirmer que tout mot assez long contient un facteur de la forme décrite par le motif. Le motif $xyx$ est inévitable, le motif $xyxyx$ est évitable, même sur deux lettres.

La notion de répétition est étendue comme suit aux répétitions fractionnaires : la période (aussi appelée période minimale) d'un mot $w=a_{1}\cdots a_{n}$ est le plus petit entier $p$ tel que $a_{i}=a_{p+i}$ pour $i=1,\ldots ,n-p$. L'exposant du mot $w$ est le quotient$n/p$ de sa longueur par sa période. Par exemple, le mot entente a période 3, il est d'exposant 7/3. L'exposant critique d'un mot infini, qui est le plus grand exposant d'un facteur du mot, dépend de la nature du mot. Un thème similaire est la couverture d'un mot par un motif ; les mots qui admettent une telle couverture sont dits mots quasi-périodiques.

L'existence d'un seuil pour les répétitions fractionnaires a été conjecturé par Françoise Dejean en 1972 ; la démonstration de ce fait est le théorème de Dejean.

La notion de répétition est aussi étendue aux répétitions dites abéliennes : ainsi un carré abélien est un mot $xy$ où $y$ est une anagramme de $x$, c'est-à-dire égal à $x$ à une permutation des lettres près ; par exemple $abba$ est un carré abélien. On peut montrer que des cubes abéliens peuvent être évités sur 3 lettres, mais que les carrés abéliens ne sont évitables que sur 4 lettres.

Une répétition maximale (en anglais un run)dans un mot est un facteur d'exposant au moins égal à 2 et qui ne peut être étendue en une répétition plus longue. Le nombre total de répétitions maximales dans un mot de longueur $n$ est au plus égal à $n$. Ce résultat, appelé le théorème des répétitions maximales, aussi appelé le « théorème des runs » a été démontré en 2015.

Mots sans carré et sans puissances

Un carré est un mot composé de deux parties égales consécutives, comme « bonbon » ou « papa ». En bio-informatique, un carré est appelé une répétition en tandem. Un mot sans carré est un mot qui ne contient pas de facteur carré. Par exemple, le mot « consécutivement » est un mot sans carré. Plus généralement, un mot sans cube et un mot sans puissance $k$-ième est un mot qui ne contient pas de cube ou de puissance $k$-ième en facteur. Il existe des mots infinis sans carré sur tout alphabet d'au moins trois lettres, comme l'a prouvé Axel Thue. Sur un alphabet à deux lettres, un tel mot n'existe pas. Le mot de Prouhet-Thue-Morse contient des carrés, en revanche il est sans cube.

Une majoration du nombre de carrés distincts (ou plus généralement de puissances d'un exposant fixe) qui sont facteurs d'un mot donné est un problème posé en 1998 par Fraenkel et Simpson, et a conduit a plusieurs développements sans être entièrement résolu.

Complexité combinatoire d'un mot

Le mot de Fibonacci, caractérisé par une droite de pente $\varphi$ ou $\varphi -1$ avec $\varphi$, le nombre d'or

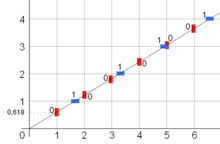
Il existe plusieurs manières de cerner la complexité d'une suite infinie de symboles. Intuitivement, ces notions doivent indiquer à quel point une suite est « compliquée » ou « complexe », ou « aléatoire », ou « chaotique ». La complexité algorithmique est une mesure qui évalue combien elle est difficile à construire. Cette difficulté est mesurée par la taille du programme nécessaire pour la construire, ou par temps qu’il faut pour calculer son n-ième terme. La théorie algorithmique de l'information fondée par Kolmogorov, Solomonoff et Chaitin aborde ces problèmes. La complexité de Kolmogorov d’une suite est la taille du plus court programme sur une machine de Turing qui engendre cette suite. La notion est relié aussi à la compressibilité d’une séquence.

Une autre mesure, plus arithmétique ou combinatoire, est la complexité « en facteurs », en anglais « subword complexity », appelé aussi complexité combinatoire. Elle mesure le nombre de facteurs qu'un mot possède pour chaque longueur. Formellement, la fonction de complexité d'un mot fini ou infini $x$ est la fonction $n\mapsto c_{x}(n)$ qui, pour chaque entier $n$, compte le nombre de facteurs $c_{x}(n)$(ou blocs) de longueur $n$ dans ce mot. Pour un mot infini $x$, un résultat dû à Ethan M. Coven et Gustav Hedlund dit que si $c_{x}(n)\leq n$ pour un entier $n$, alors le mot $x$ est ultimement périodique. Les mots infinis apériodiques de complexité minimale ont donc une fonction de complexité égale à $n+1$. Ce sont les mots sturmiens. Le plus connu des mots sturmiens est le mot de Fibonacci. Des mesures voisines sont la complexité palindromique qui mesure le nombre de palindromes, ou la complexité arithmétique.

Le terme de « complexité combinatoire », en opposition à la complexité algorithmique, est assez récent : on le trouve par exemple chez Jean-Paul Allouche ou Michel Rigo.

Mots automatiques

Les mots automatiques sont des suites que l'on peut définir à l'aide d'automates finis. La suite de Prouhet-Thue-Morse est l'exemple paradigmatique de cette famille. Les pliages de papiers en sont un autre exemple.

Mots morphiques

Un mot morphique est un mot infini obtenu par itération d'un morphisme, suivi de l'application d'un deuxième morphisme. En absence du deuxième morphisme, on parle de mot purement morphique. C'est une méthode très efficace et répandue de construction de mots infinie. Elle est « robuste » en ce sens qu'elle est stable par toute sorte d'opérations. Par exemple, le mot de Fibonacci infini est un mot purement morphique, la suite de Prouhet-Thue-Morse également. La suite caractéristique des carrés : 11001000010000001000... est morphique, mais n'est pas purement morphique.

La conjecture de Billaud est une conjecture sur la possibilité de caractériser un mot fini par certains de ses sous-mots.

Mots de Toeplitz et de Stewart

Un mot de Toeplitz est un mot infini obtenu par un processus itératif qui est décrit par une suite d'une ou plusieurs règles d'interclassement dits « motifs de Toeplitz ». Les plus connues de ces mots sont la suite des suite de pliage de papier et la suite chorale de Stewart.

Complexité abélienne

La complexité abélienne d'un mot fini ou infini est la fonction qui compte le nombre de facteurs de longueur donnée dans ce mot, à permutation de lettres près. C'est une autre mesure de la complexité combinatoire d'une suite.

Équations entre mots

Une équation de mots ou une équation entre mots (en anglais word equation) est un couple $(U,V)$ de mots, usuellement écrit sous la forme d'une équation

$U=V$.

Ici, $U$ et $V$ sont des mots composés lettres qui sont des constantes ou des variables. Les constantes sont écrits en minuscules, les variables en majuscules. Par exemple, l'équation

$abXbX=XbXba$

contient quatre occurrences de la variable $X$, et des constantes $a$ et $b$. Une solution d'une équation est un ensemble de mots sans variables, un pour chaque variable, tel que la substitution des mots aux variables rend les deux composantes de l’équation identiques. Par exemple, pour $X=a$ (et plus généralement pour $X=(ab)^{k}a$ avec $k\geq 0$, les deux côtés de l'équation deviennent égaux, à $ababa$ (et plus généralement à $(ab)^{2k+2}a$).

Un célèbre théorème de Makanin dit qu'il est décidable si une équation de mots, et plus généralement un ensemble d'équations de mots, possède une solution. En cela, les équations de mots se distinguent des équations diophantiennes pour lesquels l'existence de solutions est indécidable par le théorème de Matiiassevitch résolvant le dixième problème de Hilbert.

Un problème lié est la description de toutes les solutions d'une équation donnée, sous forme paramétrée en général. La première étude systématique dans cette direction est faite par Hmelevskii.

Récurrence

Un mot infini $x$ est récurrent si tout facteur de $x$ apparaît une infinité de fois dans $x$.

• Le mot $ab^{\omega }$ n'est pas récurrent.
• Le mot de Champernowne binaire $0100011011000001010011\ldots$ formé de la concaténation des développements binaires des entiers naturels est récurrent.
• Un mot ultimement périodique et récurrent est périodique.

Un mot infini $x$ est uniformément récurrent ou à lacunes bornées si deux occurrences consécutives d'un facteur de $x$ sont à distance bornée. Plus précisément, pour tout facteur $u$ de $x$, il existe une constante $N(u)$ telle que deux occurrences consécutives de $u$ dans $x$ sont à distance au plus $N(u)$.

• Le mot de Champernowne binaire n'est pas uniformément récurrent. En effet, deux occurrences consécutives du symbole $1$ peuvent être séparées par des séquences arbitrairement longues de $0$.
• Le mot de Fibonacci $010010100100101001010\ldots$ est uniformément récurrent. Par exemple, les occurrences du chiffre $1$ dans ce mot infini sont les éléments de la suite A001950 de l'OEIS, soit 2, 5, 7, 10, 13, 15, 18,... La distance entre deux $1$ consécutifs est donc au plus 3.
• Le mot de Thue-Morse est uniformément récurrent.

Il y a un lien entre les mots uniformément récurrents et les ensembles syndétiques. Un ensemble $S$ d'entiers naturels est appelé syndétique s'il existe un entier $N$ tel que pour deux entiers consécutifs $s<t$ de $S$, on ait $t-s<N$. Un mot infini $x$ est donc uniformément récurrent si, pour tout facteur $u$ de $x$, l'ensemble $S(u)$ des débuts d'occurrence de $u$ dans $x$ est syndétique.

La fonction de récurrence $R$ d'un mot infini $x$ donne la valeur maximale des lacunes entre occurrences consécutives de mots d'une longueur donnée. Plus précisément, $R(n)$ est le plus petit entier $N$ tel que tout facteur de $x$ de longueur $n$ soit facteur de tout facteur de longueur $N$ de $x$, formellement $R(n)=\inf\{N\mid \forall w\in F_{N}(x),F_{n}(w)=F_{n}(x)\}$ On peut voir l'entier $R(n)$ comme la largeur minimale d'une fenêtre que l'on glisse sur le mot $x$ et qui a la propriété que tout facteur de longueur $n$ figure toujours dans la section couverte par la fenêtre.

• Pour le mot de Fibonacci, on a $R(1)=3$, et $R(2)=6$; en effet, le facteur $01010$ du mot de Fibonacci ne contient pas le facteur $00$, mais tout facteur de longueur 6 contient les trois facteurs $00,01,10$ parce que $10101$ n'est pas facteur du mot de Fibonacci.

Fonction de récurrence de la suite de Prouhet-Thue-Morse

Pour le mot de Thue-Morse $01101001100101101001\ldots$, on a $R(1)=3$ (tout facteur de longueur 3 contient un $0$ et un $1$) et $R(2)=9$ (le facteur $01011010$ ne contient pas $11$). En fait, la fonction de récurrence a été calculée par Morse et Hedlund, dès 1938. Les premières valeurs sont données dans la table suivante :

Fonction de récurrence de la suite de Prouhet-Thue-Morse

$n$	1	2	3	4	5	6	7	8	9	10
$R(n)$	3	9	11	21	22	41	42	43	44	81

C'est la suite A179867 de l'OEIS. La formule de récurrence est toute simple : pour $n\geq 2$, on a $R(2n)=2R(n+1)-1$ $R(2n+1)=2R(n+1)$. Il en résulte la forme close suivante. Posons $n=2^{r}+p$, avec $2\leq p\leq 2^{r}+1$. Une telle écriture est toujours possible pour $n\geq 3$. Alors $R(n)=10\cdot 2^{r}+p-1$.

Fonction de récurrence du mot infini de Fibonacci

Cette fonction de récurrence a une expression un peu moins simple, et elle est connue depuis l'article de Morse et Hedlund de 1940. On a $R(n)=F_{N+1}+F_{N}+n-1$ où $N$ est l'entier tel que $F_{N}\leq n<F_{N+1}$. Ici, les $F_{N}$ sont les nombres de Fibonacci avec $F_{0}=0,F_{1}=1$.

Fonction de récurrence du mot infini de Fibonacci

$n$	1	2	3	4	5	6	7	8	9	10
$R(n)$	3	6	10	11	17	18	19	28	29	30

C'est la suite A183545 de l'OEIS. Cette formule s'étend à tous les mots sturmiens.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Combinatorics on words » (voir la liste des auteurs).

Voir aussi

Articles connexes

• Métrique des mots
• Problème du mot
• Théorème de périodicité de Fine et Wilf
• Congruence de Simon

Bibliographie

Histoire

• Jean Berstel et Dominique Perrin, « The origins of combinatorics on words », European Journal of Combinatorics, vol. 28,‎ 2007, p. 996–1022 (lire en ligne).
• Dominique Perrin, « Les débuts de la combinatoire des mots », séminaire EHESS,‎ 2005 (lire en ligne).

Articles de synthèse

• [1992] Klaus Ulrich Schulz (éditeur), Word equations and related topics, Springer-Verlag, 1992, 256 p. (ISBN 978-3-540-55124-9, lire en ligne) — Actes du colloque IWWERT '90, Tübingen, Allemagne, 1-3 octobre 1990
• [1997] Christian Choffrut et Juhani Karhumäki, « Combinatorics of words », dans G. Rozenberg, A. Salomaa (éditeurs), Handbook of Formal Languages, vol. 1 : Word, Language, Grammar, Springer Verlag, 1997 (ISBN 978-3-540-60420-4, présentation en ligne), p. 329-438
• [2002] Volker Diekert, chap. 12 « Makanin's Algorithm », dans M. Lothaire, Algebraic Combinatorics on Words, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 90), 2002, p. 387–442.
• [2003] Jean Berstel et Juhani Karhumäki, « Combinatorics on words - a tutorial », Bull. Eur. Assoc. Theor. Comput. Sci. (EATCS), vol. 79,‎ 2003, p. 178-228 (lire en ligne).
• [2004] Juhani Karhumäki, « Combinatorics on words: a new challenging topic », TUCS Technical Report, n^o 645,‎ 2004 (lire en ligne).
• [2015] Dominique Perrin et Antonio Restivo, « Words », dans Miklos Bona (éditeur), Handbook of Enumerative Combinatorics, Chapman and Hall/CRC, 2015, 1086 p. (ISBN 9781482220865, présentation en ligne, lire en ligne)

Lothaire

• M. Lothaire, Combinatorics on words, Cambridge University Press, coll. « Cambridge Mathematical Library », 1997, xviii+238 (ISBN 978-0-521-59924-5, DOI 10.1017/CBO9780511566097, MR 1475463, présentation en ligne)
• M. Lothaire, Algebraic combinatorics on words, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 90), 2002, 504 p. (ISBN 978-0-521-81220-7, présentation en ligne)
• (en) M. Lothaire, Applied combinatorics on words, Cambridge (GB), Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 105), 2005, 610 p. (ISBN 978-0-521-84802-2, présentation en ligne)

Berthé — Rigo

• Valérie Berthé et Michel Rigo (éditeurs), Sequences, groups, and number theory, Birkhäuser, coll. « Trends in Mathematics », 2018, xxvi+576 (ISBN 978-3-319-69151-0)
• Valérie Berthé et Michel Rigo (éditeurs), Combinatorics, words and symbolic dynamics, Cambridge, Royaume Uni, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 159), mars 2016, 496 p. (ISBN 978-1-107-07702-7)
• Valérie Berthé et Michel Rigo (éditeurs), Combinatorics, automata and number theory, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 135), 2010, 615 p. (ISBN 978-0-521-51597-9, lire en ligne)

Monographies

• (en) Jean-Paul Allouche et Jeffrey O. Shallit, Automatic sequences : Theory, applications, generalizations, Cambridge, Cambridge University Press, 2003, 571 p. (ISBN 0-521-82332-3, MR 1997038, zbMATH 1086.11015)
• Jean Berstel, Aaron Lauve, Christophe Reutenauer et Franco V. Saliola, Combinatorics on words : Christoffel words and repetitions in words, American Mathematical Society et Centre de recherches mathématiques, 2008, 504 p. (ISBN 978-1-4200-7267-9)
• Maxime Crochemore et Wojciech Rytter, Jewels of stringology : Text Algorithms, World Scientific Publishing, 2002, 310 p. (ISBN 978-981-02-4897-0, lire en ligne)
• Maxime Crochemore, Thierry Lecroq et Wojciech Rytter, 125 Problems in Text Algorithms with Solutions, Cambridge University Press, 2021, 345 p. (ISBN 978-1-108-83583-1 et 978-1-108-79885-3)
• Christophe Reutenauer, From Christoffel Words to Markoff Numbers, Oxford University Press, 2019, 156 p. (ISBN 978-0-19-882754-2, lire en ligne).

Textes historiques

• Ju. I. Hmelevskii, Equations in free semigroups, American Mathematical Society, Proceedings of the Steklov Institute of Mathematics 107 (1971), 1976, 270 p. (ISBN 978-0-8218-3007-9, MR 0393284, zbMATH 0326.02032, présentation en ligne) — Traduit de l’original russe, paru en 1971, par G. A. Kandall.

• Gennadiy S. Makanine, « The problem of solvability of equations in a free semigroup », Math. Sbornik (N.S.), vol. 103, n^o 2,‎ 1977, p. 147-236, 319 (MR 0470107) — Article complet, en russe. Traduction anglaise : Math. USSR Sbornik 32 (1977)