Homothétie
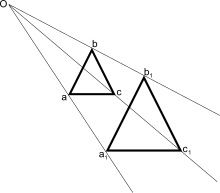
Une homothétie est une transformation géométrique par agrandissement ou réduction ; autrement dit, une reproduction avec changement d'échelle. Elle se caractérise par son centre, point invariant, et un rapport qui est un nombre réel. Par l'homothétie de centre O et de rapport k, le point M est transformé en un point N tel que
En d'autres termes, l'homothétie laisse O fixe et envoie le point M sur un point N situé sur la droite (OM) par un agrandissement ou une réduction de rapport k. Par exemple, deux poupées russes regardant dans la même direction peuvent être vues comme homothétiques.
Les homothéties de rapport non nul sont des cas particuliers de similitudes : elles multiplient les distances par la valeur absolue de leur rapport et préservent les angles.
Introduite en géométrie classique, la notion d'homothétie se généralise aux cadres des espaces vectoriels ou des espaces affines. L'ensemble des homothéties vectorielles de rapport non nul, muni de la composition, forme un groupe appelé groupe des homothéties, et l'ensemble des homothéties affines de rapport non nul et des translations muni de la composition forme également un groupe, appelé groupe des homothéties-translations.
Le terme d’homothétie, dû au mathématicien français Michel Chasles, est composé de deux éléments d'origine grecque : le préfixe homo- (ὁμός), « semblable », et thesis (θέσις), « position ». Il traduit la correspondance entre deux figures de même forme et de même orientation.
Définition en géométrie affine
[modifier | modifier le code]Dans un espace affine P (par exemple dans le plan ou l'espace usuel), pour un point donné O de P et un scalaire non nul k, on appelle homothétie de centre O et de rapport k la transformation f de P qui laisse le point O invariant et telle que, pour tout point M distinct de O :
- Les points O, M et f(M) sont alignés ;
- Le rapport algébrique vaut k :
Dans le cas le plus courant où le corps des scalaires de l'espace affine P est celui des nombres réels ou des nombres complexes, on dit qu'une homothétie de rapport k avec :
- |k|>1, est un agrandissement de rapport |k| ;
- |k|<1, est une réduction de rapport |k|.
Deux cas particuliers doivent être mentionnés :
- Si k = 1, chaque point étant invariant, l'homothétie est la transformation identité : chaque point est envoyé sur lui-même ;
- Si k = –1, l'homothétie de rapport –1 est la symétrie centrale de centre O.
À noter que si le corps des scalaires de l'espace affine P est de caractéristique égale à 2, ces deux points sont confondus.[pas clair]
Une homothétie affine de rapport non nul est une application affine qui est bijective, et son application linéaire associée est l'homothétie vectorielle de même rapport (voir plus bas).
Construction de l'homothétique d'un point
[modifier | modifier le code]En pratique (dans le cas du plan ou de l'espace usuel), pour construire l'image N = f(M) d'un point M par une homothétie f de centre O et de rapport k (N s'appelle l'homothétique de M), il faut tracer la droite (OM), puis:
- si k est positif, placer sur (OM) le point N tel que le sens de O vers M soit le même que celui de O vers N et tel que la longueur du segment [ON] soit égale à k fois la longueur du segment [OM];
- si k est négatif, placer sur (OM) le point N tel que le sens de O vers M soit l'opposé que celui de O vers N et tel que la longueur du segment [ON] soit égale à |k| fois la longueur du segment [OM];
Alors N est l'homothétique de M.
Propriétés affines
[modifier | modifier le code]- Toute homothétie transforme une droite en une droite qui lui est parallèle.
Sans utiliser le théorème de Thalès, si h est une homothétie de centre O envoyant les points M et N sur f(M) et f(N), alors la relation de Chasles donne :
- .
En particulier, les droites (f(M)f(N)) et (MN) ont même droite vectorielle directrice ; elles sont donc parallèles. Les homothéties affines de rapport non nul sont, avec les translations, les seules applications de l'espace affine dans lui-même ayant cette propriété. Ceci permet une caractérisation purement géométrique des homothéties en dimension au moins 2 : ce sont les applications affines qui transforment une droite en une droite parallèle et qui ont au moins un point fixe.
- Toute homothétie préserve le parallélisme : deux droites parallèles sont envoyées sur deux droites parallèles.
En effet, si deux droites d et d' sont parallèles, et que h est une homothétie, alors par la propriété précédente, h(d) et d sont parallèles, et h(d') et d' sont aussi parallèles. Par transitivité, les droites h(d) et h(d') sont donc parallèles.
- Toute homothétie préserve les rapports algébriques.
Si M, N, P et Q sont quatre points alignés, et que h est une homothétie de rapport k, il a été obtenu :
- .
Si PQ=u MN, alors, comme k est non nul, h(P)h(Q) = u h(M)h(N). Donc, h préserve les rapports algébriques.
Théorème de Thalès
[modifier | modifier le code]Les propriétés citées ci-dessus sont une reformulation du théorème de Thalès[1] :
En reprenant les notations du théorème cité, si les points A et N sont les images respectives des points B et M par la même homothétie de centre O, l'égalité des rapports algébriques est vérifiée. Le sens réciproque implique que les droites (AN) et (BM) sont parallèles. Le théorème de Thalès montre que toute homothétie transforme une droite en une droite qui lui est parallèle.
Par ailleurs, le théorème de Thalès montre qu'il existe exactement une unique homothétie de centre O envoyant M sur N. Cette homothétie envoie tout point B non aligné avec O, M et N sur le point d'intersection de la droite (OB) avec la parallèle à (BM) passant par N. La construction de l'image d'un point de la droite (OM) nécessite de construire au préalable l'image d'un point non aligné avec O, M et N.
Composition
[modifier | modifier le code]

La composée de deux homothéties de centre O et de rapports k et k' est une homothétie de centre O et de rapport kk'. L'ensemble des homothéties de centre O est donc stable par composition : il forme un sous-groupe commutatif du groupe des transformations de l'espace.
La composée de deux homothéties de centres différents O et O' et de rapports k et k' est :
- une translation de vecteur si le produit kk' vaut 1 ;
- une homothétie de rapport kk' et de centre O'' barycentre des points (O, kk'–k') et (O', k'–1) si kk' est différent de 1.
La composée t o h d'une homothétie de centre O et de rapport k et d'une translation de vecteur u est aussi une homothétie de rapport k et de centre O'' barycentre des points (O, k) et (O', -1) où O' est le point tel que . Enfin, la composée h o t est une homothétie de rapport k et de centre O'' barycentre de (O', k) et (O, –1) où O' est le point tel que .
Ces propriétés montrent que l'ensemble des homothéties et des translations est stable par composition ; il forme un sous-groupe non commutatif du groupe des transformations de l'espace.
Propriété en géométrie euclidienne
[modifier | modifier le code]En géométrie euclidienne, la composée d'une rotation de centre O et d'une homothétie de centre O s'appelle une similitude de centre O. Comme toutes les similitudes, les homothéties vérifient les propriétés suivantes :
- Toute homothétie préserve les angles, et donc en particulier l'orthogonalité. Une homothétie est donc une transformation conforme ;
- Une homothétie transforme un cercle en un cercle ;
- Une homothétie de rapport k modifie les distances par un facteur et modifie les volumes par un facteur où n est la dimension de l'espace.
Dans le plan complexe
[modifier | modifier le code]Par l'homothétie de centre A d'affixe a et de rapport k, le point M d'affixe z a pour image le point M' d'affixe z' vérifiant :
- .
Figure caractéristique du trapèze
[modifier | modifier le code]
Si ABCD est un trapèze tel que avec k différent de 1, il existe deux homothéties transformant [AB] en [CD] : une de centre O' intersection des diagonales et de rapport –k et l'autre, de centre O intersection des droites (AD) et (BC) et de rapport k.
Géométrie vectorielle
[modifier | modifier le code]Dans un espace vectoriel V sur un corps commutatif, on appelle homothétie de rapport le scalaire k l'application k.id, qui à tout vecteur v associe le vecteur kv. C'est un endomorphisme de V. Si V est de dimension finie n, la matrice de k.id, dans n'importe quelle base de V, est la matrice scalaire k.In où In est la matrice identité de taille n.
L'unique valeur propre de k.id est k.
Pour deux espaces vectoriels E et F et deux applications linéaires f et g de E dans F, si f(x) est un multiple de g(x) pour tout vecteur x de E, alors[2] f est la composée de g par une homothétie de F.
En particulier, un endomorphisme h de V est une homothétie si (et seulement si) tous les vecteurs non nuls de V sont propres pour h.
On en déduit facilement qu'un endomorphisme h de V est une homothétie si (et seulement si) h commute à tout endomorphisme de V, ou même seulement[3] à toute projection sur une droite, ou encore, à tout élément du groupe spécial linéaire SL(V).
Références
[modifier | modifier le code]- François Liret et Dominique Martinais, Mathématiques pour le DEUG : algèbre 1re année : Cours et exercices avec solutions, Dunod, (ISBN 978-2-10-003149-8), p. 183.
- Voir par exemple .
- Voir par exemple .
Bibliographie
[modifier | modifier le code]Jacqueline Lelong-Ferrand, Fondements de la géométrie, Paris, PUF, , 287 p. (ISBN 2-13-038851-5)













