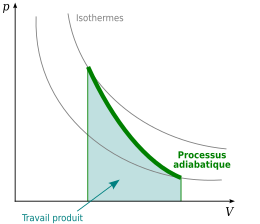
Compression et détente adiabatiques
La compression et la détente adiabatiques sont des transformations thermodynamiques décrivant le comportement de fluides, notamment de gaz, soumis à des variations de pression. Un processus adiabatique est caractérisé par l'absence d'échange de chaleur entre le système considéré et le milieu extérieur.
Principe[modifier | modifier le code]
En raison du premier principe de la thermodynamique, si un système échange du travail avec le milieu extérieur par l'intermédiaire des forces de pression, son énergie interne varie, particulièrement les énergies cinétiques microscopiques constituant l'agitation thermique des particules du système, définissant la température à l'échelle macroscopique.
Cela se traduit par une variation de la température :
- lors d'une compression, la température augmente puisque le milieu extérieur fournit du travail au système, ce qui augmente son énergie interne et donc son agitation thermique ;
- lors d'une détente, la température diminue car c'est le système qui fournit du travail au milieu extérieur.
Dans un processus adiabatique, si la température du système augmente ou diminue, il ne peut pas atteindre l'équilibre thermique avec le milieu extérieur. Cette condition se réalise si :
- le système est isolé du milieu extérieur, par une enceinte adiabatique (par exemple un calorimètre) ;
- la transformation est rapide alors que les échanges de chaleur sont très lents.
Modélisation mathématique[modifier | modifier le code]
Réversibilité[modifier | modifier le code]
Les processus adiabatiques sont en général modélisés mathématiquement par des gaz parfaits avec lesquels les opérations sont réversibles et dites « isentropiques », c'est-à-dire à entropie constante. À basse pression, cette approximation est acceptable, mais dans la réalité, l’entropie du système augmente toujours au moins un peu. Le système est alors dit « isenthalpique » car, même si l’entropie augmente, l’énergie totale du système (enthalpie) est, elle, préservée.
Pour expliquer ce phénomène, prenons un cylindre rempli d’un gaz que l'on va comprimer avec un piston. Dans un système réversible (donc théorique), si on comprime le gaz avec le piston et qu’on le relâche, le piston va revenir exactement dans sa position d’origine et le gaz, après l’échauffement de sa compression puis sa détente, va revenir exactement dans le même état thermodynamique (même température, même pression) qu’à l’origine. Dans la réalité, par contre, la compression va nécessiter un effort supplémentaire qui sera perdu en chaleur à cause de la viscosité du gaz. Et lors de la détente, le travail rendu sera un peu diminué par cette même viscosité.
À la fin du cycle, le gaz sera un petit peu plus chaud et occupera un volume légèrement plus grand qu’au début ; cependant, comme les forces fournies par la détente auront été plus petites que celles requises pour la compression, le travail total rendu sera inférieur au travail fourni initialement et la différence correspondra à l’énergie absorbée par le gaz pour élever sa température.
Formule[modifier | modifier le code]
Dans un système thermodynamique fermé, toute variation de l’énergie interne du système est égale à la somme du travail mécanique et du transfert thermique , échangés avec le milieu extérieur :
Par hypothèse, il n'y a pas d'échange avec le milieu extérieur et le terme est nul. En transformant les expressions pour chacun de ces termes et en prenant en compte que le processus est isentropique à partir des relations suivantes :
on obtient les relations suivantes :
- avec :
- , pression ;
- , volume ;
- , température absolue ;
- , masse ;
- , constante universelle des gaz parfaits ;
- , constante spécifique du gaz parfait, ;
- , masse moléculaire du gaz ;
- , masse volumique ;
- , capacité thermique à pression constante ;
- , capacité thermique à volume constant ;
- , indice adiabatique, .
Le travail mécanique mis en jeu est le produit de la variation de volume par la pression extérieure exercée pour ce changement de volume.
La variation correspondante d'enthalpie () est donné par la différentielle:
Pour que le processus soit à la fois réversible et adiabatique, il faut que donc . Ces processus sont donc isentropiques pour un gaz parfait ce qui mène à :
Or pour un gaz parfait l'énergie interne et l'enthalpie ne dépendent que de la température.
avec et qui sont respectivement les capacités thermiques à volume et pression constantes.
D'où
- .
En faisant le rapport suivant :
Comme est constant pour un gaz parfait, les équations se simplifient :
En utilisant la loi des gaz parfaits ,
Une autre forme de cette formule permet de calculer la température de refoulement d'un compresseur en supposant que la compression est adiabatique et réversible[1] :
avec
- : pression de refoulement du compresseur en bars ;
- : pression d'aspiration du compresseur en bars ;
- : indice adiabatique, qui dépend du gaz (gaz parfait) (pour de l'air, vaut environ 1,4 à 15 °C) ;
- : température d'aspiration du compresseur en °C ;
- : température de refoulement du compresseur en K.
Sur une pompe à vélo avec de 2 bar, de 1 bar et de 293,15 K (20 °C), la température en sortie de la pompe sera 84 °C (ceci est purement un calcul théorique car dans la réalité ce sera moins, l'échange ne sera pas complètement adiabatique et la pompe s'échauffera, prenant une partie de l'énergie dégagée).
Diagrammes thermodynamiques[modifier | modifier le code]
On peut calculer mathématiquement l'énergie et les changements de pression du processus mais en général on utilisera une représentation d'une transformation adiabatique sur des diagrammes thermodynamiques. Ces diagrammes sont pré-calculés pour indiquer le chemin pression versus température suivi. Les quatre diagrammes thermodynamiques utilisés pour analyser la structure thermique de l'atmosphère sont ainsi le téphigramme, le Skew-T, l'émagramme et le diagramme de Stüve.
Applications[modifier | modifier le code]
La compression adiabatique permet d'expliquer l'échauffement de la pompe à vélo, ainsi que le fait que l'air qui sort lorsque l'on dégonfle un pneu soit froid (même si la transformation n'est pas strictement adiabatique). Elle permet aussi d'expliquer le risque du « coup de feu » dans les détendeurs de dioxygène : lorsque l'on ouvre la bouteille, la pression augmente en aval du détendeur et provoque un échauffement ; si le détendeur contient un corps inflammable (corps gras, joint non conforme), il s'enflamme (il est en présence de 100 % de dioxygène) et provoque une oxydation exothermique du métal avec un effet similaire à un chalumeau, qui perfore le détendeur (oxycoupage).
La détente adiabatique est utilisée dans les réfrigérateurs, climatiseurs et groupes frigorifiques, pour refroidir.
La détente adiabatique est également utilisée pour la dessiccation dans le procédé de détente instantanée contrôlée (DIC).
En météorologie, la compression et la détente adiabatique avec l'altitude (voir l'article Variation de la pression et de la température atmosphériques avec l'altitude) provoque une variation de température de la masse d'air qui conditionne de nombreux phénomènes atmosphériques, voir l'article Gradient thermique adiabatique.
Remarque de terminologie[modifier | modifier le code]
L'antonyme du mot adiabatique est diabatique. Pour des raisons historiques, dont le calque sur l'anglais, le terme non-adiabatique reste néanmoins largement répandu dans la littérature scientifique.
Notes et références[modifier | modifier le code]
- M. Graille, Utilisateur et choix des compresseurs : Conception, construction et exploitation des réseaux de transport de gaz, Gaz de France, 184 p. (lire en ligne), p. 15.