Électromouillage

En physique, l'électromouillage est la modification des propriétés de mouillage d'une surface généralement hydrophobe par l'application d'une tension électrique entre un solide et un liquide conducteur (électrolyte). Ce phénomène physique relève du domaine de la microfluidique, c'est-à-dire de la manipulation des liquides à petite échelle. Par la formation d'une capacité électrique, l'énergie apportée vient modifier le bilan énergétique qui détermine la forme de la goutte, celle-ci peut alors se déformer ou être déplacée.

En 1875, Gabriel Lippmann observe une modification de la montée capillaire entre deux plaques en appliquant une tension électrique. Il utilise cette propriété pour réaliser un électromètre très précis pour l'époque. Ce phénomène, nommé électromouillage entre-temps, connaît un regain d'intérêt dans les années 1990, les progrès de la microtechnologie ayant ouvert de nouvelles opportunités d'applications. Il permet aujourd'hui de réaliser, entre autres, des lentilles optiques à focale variable ou du papier électronique.

Manifestations du phénomène

L'électromouillage appartient au domaine de la microfluidique, c'est-à-dire qu'il concerne des gouttes de dimensions submillimétriques. La plupart des expériences publiées s'intéressent à des gouttes dont le diamètre se situe entre 100 µm et 1 mm^[1]. À cette échelle, la tension superficielle comme la capacité électrique créent une énergie proportionnelle à la surface de la goutte qui devient, lorsque les dimensions augmentent, négligeable face aux effets du poids qui, lui, est proportionnel au volume. Physiquement, on dit que le nombre d'Eötvös est très petit devant 1, ce qui signifie que le poids devient négligeable devant les forces capillaires mises en jeu.

Dans cette première section de l'article, une première approximation du phénomène, reposant sur un certain nombre d'hypothèses simplificatrices, notamment le fait que la dérivée de la capacité par rapport à la surface est constante et que le liquide est parfaitement conducteur^[2], est décrite dans différents cas. La deuxième section abordera des cas où certaines de ces hypothèses ne sont plus vérifiées.

Étalement d'une goutte

Deux schémas présentant l'électromouillage. — Principe de l'électromouillage : la tension appliquée entre le liquide (vert) et le substrat (bleu), les deux étant séparés par une couche isolante (vert jaune), crée une capacité électrique qui modifie la forme de la goutte.

La figure ci-contre représente le phénomène d'électromouillage dans sa manifestation la plus simple. Une goutte de liquide conducteur (représentée arbitrairement en vert) est déposée sur une couche isolante (vert jaune), elle-même posée sur un substrat conducteur (bleu). Le substrat est isolant et suffisamment hydrophobe pour que le mouillage ne soit pas total : le liquide forme une goutte et ne s'étale pas. L'électrode qui doit relier la goutte n'est pas représentée ici.

Lorsqu'une tension est appliquée entre le substrat et le liquide, le bilan énergétique fait intervenir deux types d'énergie : l'énergie de mouillage des espèces concernées, et l'énergie électrique stockée dans la capacité. Puisque le système présente deux conducteurs séparés par un isolant, une capacité électrique se forme et modifie le mouillage, et donc la forme de la goutte.

En l'absence de diélectrique, si le liquide est posé directement sur le métal, il existe tout de même une capacité, déterminée par l'effet de double couche électrique^[3].

Calcul

La capacité créée autour du diélectrique vaut par unité de surface :

C_{s}={\frac {\epsilon _{0}\epsilon _{r}}{t}}

où

є₀ est la permittivité de référence,
є_r est la permittivité relative du diélectrique,
$t$ est son épaisseur.

La tension appliquée est notée $V$ , et, pour une variation infinitésimale $\delta S$ de la surface de la goutte, l'énergie électrostatique stockée dans la goutte varie de :

{\frac {C_{s}V^{2}\delta S}{2}}

tandis que la source électrique fournit un travail égal à :

-C_{s}V^{2}\delta S

il y a donc une variation d'énergie électrique globale de $-{\frac {C_{s}V^{2}\delta S}{2}}$ . La goutte tend à minimiser l'énergie électrique totale en s'étalant^[4].

En prenant en compte la force dérivant de cette énergie électrique en plus des tensions de surface, on modifie la loi de Young-Dupré, laquelle détermine l'angle de contact au bord de la goutte en situation d'équilibre. Lorsque la ligne de contact est à l'équilibre, les composantes horizontales des forces s'y appliquant doivent s'annuler, soit :

\gamma _{2}\cos \theta +\gamma _{1}=\gamma _{3}+{\frac {C_{s}V^{2}}{2}}

Cette équation est connue comme l'équation de Young-Lippmann, où

$\gamma _{1}$ est la tension superficielle entre l'isolant et le liquide,
$\gamma _{2}$ est la tension de surface entre le liquide conducteur et le milieu ambiant (air par exemple),
$\gamma _{3}$ est la tension de surface entre l'isolant et le milieu ambiant,
$\theta$ est l'angle de contact, défini comme sur la figure.

Le bilan des forces appliquées sur la ligne de contact apparaît sur la figure, avec la réaction R du substrat.

Ce dont on déduit l'expression du cosinus de l'angle de contact^[5] :

\cos \theta =\left({\frac {\gamma _{3}-\gamma _{1}+{\frac {C_{s}V^{2}}{2}}}{\gamma _{2}}}\right)\,

On peut aussi exprimer cette relation sous la forme :

\cos \theta =\cos \theta _{0}+{\frac {C_{s}V^{2}}{2\gamma _{2}}}\,

où $\theta _{0}$ est l'angle de contact « au repos » (sans différence de potentiel électrique), et le terme ${\frac {C_{s}V^{2}}{2\gamma _{2}}}$ , parfois appelé « nombre d'électromouillage »^[6] exprime le ratio du phénomène électrostatique par rapport à la tension superficielle. C'est un nombre adimensionnel.

La tension électrique intervient au carré ; ainsi l'application d'une tension, qu'elle soit positive ou négative, tend toujours à « étaler » davantage le liquide sur la surface.

Goutte isolante en milieu liquide conducteur

Ici la goutte observée (vert) est un liquide diélectrique (par exemple une huile minérale) entourée d'un liquide conducteur (tel une solution aqueuse), les deux liquides devant bien sûr être non miscibles. Lorsqu'une tension est appliquée entre l'eau et le substrat, la surface de contact tend comme précédemment à augmenter, mais cela se traduit ici par un relèvement de la goutte. La position initiale des liquides est réglée en jouant localement sur l'hydrophilie de la surface^[7].

Modification de la montée capillaire

Une autre manifestation de l'électromouillage est celle mise en évidence par Henri Pellat. Dans le dispositif illustré ci-contre, deux électrodes parallèles sont partiellement immergées dans un liquide isolant (huile par exemple), de permittivité relative $\kappa _{1}$ , et de masse volumique $\rho$ .

Du fait des forces capillaires, le liquide va monter ou descendre entre les deux plaques, selon son énergie de mouillage au contact des électrodes. Si une tension est appliquée entre les électrodes, on emmagasine de l'énergie électrique dans la capacité formée entre elles. Comme dans le cas précédent, cette énergie va modifier la position d'équilibre^[8]^,^[9].

En écrivant les variations d'énergie (énergie électrique et énergie potentielle de gravité) dues à un changement $\delta h$ de la hauteur du liquide et en cherchant l'équilibre, on obtient la montée due à la tension électrique, qui s'ajoute à la montée capillaire proprement dite^[8] :

$h=h_{cap}+{\frac {(\kappa _{1}-1)\epsilon _{0}V^{2}}{2\rho gD^{2}}}$

Où g est la pesanteur. Ici encore, la tension intervient au carré, l'effet est donc toujours une montée supplémentaire, que la tension soit positive ou négative.

Déplacement de goutte

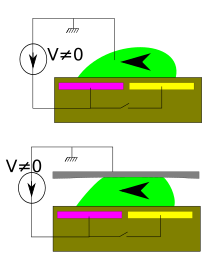
Le principe de déplacement d’une goutte est illustré dans l’image ci-contre. Une différence de potentiel est appliquée entre la goutte et l'électrode de gauche (violet), celle de droite (jaune) est laissée flottante (c'est-à-dire déconnectée du circuit électrique). Il en résulte une forme asymétrique de la goutte, car les angles de contact sont différents, et surtout un bilan des forces non nul (la composante ${\frac {C_{s}V^{2}}{2}}$ n'étant présente que d'un côté), qui déplace la goutte vers la gauche. En pratique, la goutte est « attirée » par l'électrode active. C'est sur ce principe que l'on peut déplacer des gouttes, par un réseau d'électrodes activées séquentiellement^[11].

Électromouillage sur film perméable

Dans la variante EWOLF (electrowetting on liquid-infused film), la surface de l'isolant est une membrane perméable (en PTFE dans les premiers travaux publiés) imprégnée d'une huile jouant un rôle de lubrifiant. Cette forme d'électromouillage présente des caractéristiques intéressantes : la réversibilité est bien meilleure, et les oscillations transitoires des gouttes sont réduites^[12].

Phénomène inverse

Le phénomène inverse associé à l'électromouillage (REWOD : reverse electrowetting on dielectric) a été décrit dans les années 2000 par Tom Krupenkin et Ashley Taylor. Considérons une goutte de liquide conducteur placée en vis-à-vis d'une électrode, dont elle est séparée par un diélectrique. Le dispositif est polarisé, c'est-à-dire qu'une différence de potentiel est appliquée entre la goutte et l'électrode. Si une force mécanique est appliquée, forçant la goutte à se déplacer, ce déplacement réduit la surface en vis-à-vis et donc la capacité, produisant un déplacement de charges électriques. La goutte revient ensuite à sa position initiale, créant un courant dans le sens inverse. Si cette opération (déplacement de la goutte et retour à sa position initiale) est répété, l'intégrale sur un cycle de la puissance créée par le déplacement de charges est non nulle, il y a donc une production nette d'énergie^[13].

Cas particuliers

Le phénomène est en réalité plus complexe que décrit précédemment. Cette section regroupe les cas qui s'éloignent du modèle de premier ordre.

Angle de contact local

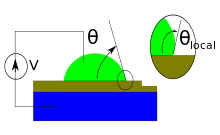
À l'échelle microscopique, la surface de la goutte peut présenter une courbure différente au pied de la goutte, et l'angle de contact local peut être différent de celui observé macroscopiquement, comme illustré ci-contre. Ce phénomène s'explique par la présence de lignes de champ quasi-horizontales dans cette zone, et de charges électriques dans le liquide. La force de Coulomb exercée sur le fluide modifie la forme de la goutte (très localement) jusqu'à être compensée par la pression de Laplace. L'équation ci-dessus donnant l'expression de $\cos {\theta }$ reste vraie mais s'applique à l'angle de contact apparent (à l'échelle de l'ensemble de la goutte), tandis que l'angle local obéit à d'autres lois^[1] : il tend en réalité à rester constant, égale à $\theta _{0}$ .

Pour déterminer la forme de la goutte, il faut noter qu'en tout point de sa surface, il existe en régime stationnaire un équilibre entre plusieurs termes de pression : électrostatique (tenseur des contraintes de Maxwell), gravitationnelle, et pression de Laplace. Cet équilibre s'écrit^[14] :

$-{\rho }gz+\gamma _{2}({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}})+{\frac {\epsilon _{0}\epsilon _{r}E_{n}^{2}}{2}}+\Delta P=0$

Avec

$E_{n}$ la composante du champ électrique normale à la surface
$\Delta P$ le saut de pression entre l'intérieur et l'extérieur de la goutte
$R_{1}$ et $R_{2}$ le rayon de courbure de la surface de la goutte selon deux directions orthogonales.

$E_{n}$ est négligeable, sauf au voisinage immédiat de la ligne de contact. À proximité immédiate de celle-ci (dans une zone dont la hauteur est du même ordre de grandeur que l'épaisseur $d$ du diélectrique), le terme dépendant de $E_{n}$ vient modifier la courbure, ce qui explique la différence entre l'angle apparent et l'angle local.

Comportement en fréquence

Si la tension appliquée est alternative, le comportement de la goutte dépend de la fréquence. En basse fréquence, elle se déformera en suivant le carré de la tension instantanée, c'est-à-dire qu'elle sera toujours en position d'équilibre. En haute fréquence, les phénomènes d'écrantage font que le liquide ne se comporte plus comme un conducteur (et l'électromouillage disparaît). Dans une gamme de fréquence intermédiaire, c'est simplement la valeur efficace du signal appliqué qui intervient dans l'équation^[15].

Dans le cas d'une solution aqueuse, l'effet de l'électromouillage commence à diminuer vers 1 kHz, après une période de transition d'environ une décade il disparaît, laissant place à un autre phénomène, la diélectrophorèse^[8]^,^[16].

Comportement en haute tension

L'équation de Young-Lippmann est valide jusqu'à une certaine limite en tension, où un phénomène de saturation apparaît. Cela empêche d'atteindre une situation de mouillage total que l'équation permettrait, en élevant la tension au point que le terme de droite de l'équation devient supérieur à 1^[17]. Plusieurs mécanismes explicatifs (qui ne sont pas mutuellement exclusifs et dont l'ordre d'importance peut changer selon la situation) ont été avancés pour ce phénomène, notamment une limite thermodynamique de la tension de surface effective (qui ne pourrait devenir négatif), l'ionisation du milieu ambiant par la singularité de champs électriques au voisinage de la ligne de contact, ou le fait que les fuites du diélectrique deviennent non négligeables^[18].

La valeur à laquelle ce phénomène se présente dépend, notamment, des caractéristiques de la couche diélectrique (épaisseur, permittivité, tension de surface). Dans le cas assez typique où on étudie solution aqueuse sur une couche de teflon de 2,4 μm les mesures « décrochent » de la loi théorique pour une tension de 109 volts^[19].

En 2015 un modèle prédisant assez bien le phénomène de saturation a été présenté^[20]. Dans ce modèle, tant le diélectrique que le liquide sont présentés comme des conducteurs imparfaits et la répulsion entre les charges accumulées dans l’un et l'autre explique la saturation.

En outre, à l'approche de la saturation, l'électromouillage peut devenir asymétrique, c'est-à-dire que des angles de contacts différents sont obtenus pour les tensions $+V$ et $-V$ ^[21].

Lorsque la tension appliquée est importante, l'effet de pointe électrostatique crée un champ électrique localement plus important dans le diélectrique immédiatement sous la ligne de contact. Ainsi peut-il apparaître à cet endroit une accumulation de charges dans le diélectrique, voire un claquage diélectrique^[22].

Comportement hystérétique et force minimale

Idéalement, l'électromouillage est un phénomène parfaitement réversible. Cependant, en pratique, il peut présenter un comportement hystérétique, c'est-à-dire si la tension est modifiée et ramenée à sa valeur initiale, la forme de la goutte reste modifiée. Ce comportement s'explique par les forces d'épinglage dues aux inhomogénéités, à l'échelle microscopique, de la surface : chaque inhomogénéité crée un obstacle que la ligne de contact doit franchir au prix d'une dépense énergétique. C'est pour cette même raison qu'il existe, pour le déplacement de goutte, une force minimale à exercer en dessous de laquelle la goutte ne se déplace pas^[23].

Pour réduire cet effet de seuil et cette hystérésis, qui pénalisent les applications, il existe plusieurs stratégies. La plus évidente est de chercher à obtenir la surface la plus homogène possible. Une autre méthode est d'utiliser une tension alternative, les vibrations qu'elle induit dans la ligne de contact aidant à franchir les obstacles^[24]^,^[23]. Enfin, utiliser un contact « liquide sur liquide » est très efficace^[12].

Combinaison avec d'autres effets

Optoélectromouillage

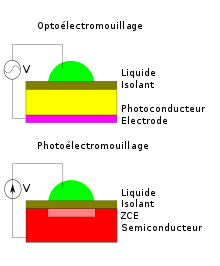
Dans un dispositif d'optoélectromouillage, on cumule le principe de l'électromouillage avec l'utilisation d'un photoconducteur, c'est-à-dire un matériau dont la résistivité électrique diminue sensiblement lorsqu'il est exposé à la lumière. On crée ainsi un pont diviseur de tension, avec en série la résistance de la couche photoconductrice et la capacité sous la goutte — il faut donc appliquer une tension alternative pour que l'effet diviseur soit présent. Lorsque le photoconducteur est exposé à la lumière, sa résistivité diminue et la tension « vue » par la goutte augmente, ce qui accroît l'effet de l'électromouillage. Localisé, cet effet permet par exemple de déplacer des gouttes à l'aide d'un rayon laser^[25].

Photoélectromouillage

Le photoélectromouillage est légèrement différent parce qu'il utilise non pas un matériau photoconducteur, mais la capacité créée par une photodiode. Une zone de charge d'espace est présente sous la goutte, ce qui crée un pont diviseur capacitif. La présence d'un rayon lumineux incident réduit l'étendue de cette zone en libérant des porteurs (principe de la photodiode), augmentant la capacité correspondante, et ici encore augmente le mouillage^[26].

Électro-élasto-capillarité

L'élasto-capillarité est la faculté des forces capillaires à déformer des solides élastiques à petite échelle^[27]. Ainsi, une goutte posée sur un substrat à faible module d'Young aura tendance à déformer celui-ci pour créer une forme de cuvette, tandis qu'une goutte présente entre deux fines lamelles flexibles pourra les coller l'une à l'autre^[28].

L'électro-élasto-capillarité consiste à combiner cet effet avec l'électromouillage pour le rendre pilotable et réversible^[29]^,^[30].

Utilisation d'une surface superhydrophobe

Article connexe : surface superhydrophobe.

Les performances des systèmes à électromouillage sont considérablement augmentées si les gouttes sont placées sur une surface structurée superhydrophobe, c'est-à-dire présentant de très grandes valeurs de $\gamma _{1}$ . En effet, avec une valeur initiale très grande de $\theta$ , on dispose de plus de marge pour faire jouer l'effet de l'électromouillage. C'est ainsi que la vitesse de déplacement des gouttes a pu être portée à 460 mm/s dans certains dispositifs^[10].

Histoire

Schéma en noir et blanc de l'électromètre de Lippmann. — L'électromètre de Lippmann.

Gabriel Lippmann est considéré comme le découvreur de ce phénomène qu'il a mis en évidence en 1875^[17], le liquide conducteur qu'il utilisait était le mercure. Lippmann a non seulement observé le phénomène, mais l'a théorisé (l'équation donnée précédemment est souvent appelée équation de Lippmann) et en a expérimenté les premières applications, notamment la mise au point d'un électromètre basé sur ce principe, si sensible qu'il a permis, quelques années plus tard, d'enregistrer le premier électrocardiogramme de l'histoire^[4]. C'est l'objet de sa thèse de doctorat, intitulée Relations entre les phénomènes électriques et capillaires qu’il a soutenu le 24 juillet 1875^[31] ; ses recherches sont également publiées dans les Annales de chimie et de physique la même année^[32].

Peu après, Antoine Breguet met au point un téléphone à mercure, reprenant le principe découvert par Lippmann : dans ce téléphone, la vibration de la surface liquide, enregistrée ou commandée par l'effet d'électromouillage, assure la transduction électro-acoustique^[33].

Dans ces premiers essais, le liquide est en contact direct avec le substrat conducteur. La différence de potentiel qui peut être appliquée est limitée à moins d'un volt, car dans une solution aqueuse, le phénomène d'électrolyse se manifeste rapidement^[17]. L'électromouillage fait l'objet d'un intérêt renouvelé dans les années 1990 avec des travaux comme ceux de Bruno Berge (ENS Lyon), l'utilisation d'un film mince isolant permettant d'appliquer des tensions importantes sans déclencher d'électrolyse. Dans ce cas, la valeur $t$ dans l'équation ci-dessus est l'épaisseur physique du diélectrique, en remplacement de la longueur de Debye, il faut donc compenser en appliquant des tensions plus importantes^[34].

Le terme « électromouillage » apparait d’abord en anglais en 1981 (electrowetting) : Gerardo Beni et Susan Hackwood le créent pour nommer un effet utilisé dans la conception d’un nouveau dispositif d’affichage, pour lequel ils ont déposé un brevet^[35]. Le mot apparait l’année suivante en français comme traduction du terme anglais^[36].

Applications

L'électromouillage permet de déformer et de déplacer des gouttes à l'échelle submillimétrique, de façon aisée à contrôler électroniquement, et sans phénomène de vieillissement. Ces avantages lui ont ouvert de nombreuses applications, sur lesquelles la recherche s'est énormément développée au début du XXI^e siècle^[1], souvent rendues possibles par le développement des microtechnologies^[3].

Lentilles à focale variable

Article détaillé : lentille à focale variable.

Une application de ce phénomène physique est la réalisation de lentilles à focale variable pour l'optique^[37]. Une cavité cylindrique est remplie de deux liquides présentant les caractéristiques suivantes : l'un est conducteur, l'autre isolant ; les deux sont immiscibles et ils présentent un écart d'indice optique. L'hydrophobie permet de séparer les deux liquides, leur interface forme un ménisque qui joue le rôle de lentille. En appliquant une différence de potentiel, l'électromouillage vient modifier la courbure du ménisque et donc la focalisation. Des lentilles de ce type sont sur le marché pour diverses applications, elles sont plus compactes et consomment moins d'énergie que des optiques classiques (modifiant la focalisation par déplacement mécanique des lentilles)^[38].

Laboratoires sur puce

Déplacement de gouttes par électromouillage, dans une application en biologie.

Article détaillé : laboratoire sur puce.

Une autre application est le transport goutte à goutte de liquide dans les laboratoires sur puce. Une succession d'électrodes sont utilisées pour transporter les produits par goutte, les amener sur les sites d'analyse, ou les mélanger^[39]. L'isolant est recouvert d'une surface hydrophobe (telle du SU-8 ou Teflon). Les tensions utilisées sont typiquement de quelques dizaines de volts^[21].

Technologie d'affichage

L'une des technologies de papier électronique utilise l'électromouillage. Dans cette technologie d'affichage, chaque pixel est matérialisé par un cadre de matériau hydrophobe dans lequel se situe une gouttelette d'huile (noire ou colorée), en vis-à-vis avec de l'eau déionisée. L'application d'un potentiel électrique permet d'étaler l'huile pour occuper tout le pixel, ou au contraire de lui faire prendre la forme d'une goutte très relevée, rendant le pixel quasiment transparent. Pour réaliser un affichage couleur, on superpose trois niveaux correspondants aux couleurs primaires. Ce type d'affichage est intéressant pour sa flexibilité, sa faible consommation électrique (la consommation est nulle sur un affichage fixe) et sa rapidité^[40].

Cette technologie est notamment développée par Liquavista, initialement issue de Philips, rachetée depuis par Samsung puis par Amazon.com qui compte utiliser cette technologie pour des liseuses^[41].

Pilotage de faisceaux lumineux

Une autre application est la réalisation de prismes pilotables pour des applications optiques, notamment pour le pilotage d'un faisceau dans une application Lidar. Un canal rectangulaire est empli de liquide, et des électrodes sur deux faces permettent de modifier l'inclinaison de la surface du liquide avec un temps de réaction de l'ordre de la milliseconde^[42]. Cette technologie a été présentée pour la première fois en 2006, et en 2009 un procédé de fabrication industriel pour des dispositifs de ce type a été publié^[43].

Récupération d'énergie

Le phénomène inverse est utilisé comme méthode de récolte d'énergie. Le déplacement périodique de gouttes, actionné mécaniquement (par vibration, forces de cisaillement ou différentiel de pression), est utilisé pour créer une capacité variable, laquelle engendre le déplacement de charges^[13]. Les dispositifs construits sur ce principe délivrent, pour un encombrement donné, une puissance bien plus élevée que les autres technologies de récupération d'énergie. Des projets en cours visent à développer cette technologie pour l'intégrer dans des chaussures, afin de produire de l'énergie pour alimenter des appareils mobiles^[44].

Annexes

Articles connexes

Bibliographie

Rachid Malk, Écoulements en gouttes activées par électromouillage (thèse de doctorat), Université Grenoble Alpes, 2006, 246 p. (lire en ligne)
(en) Fatima H Labeed, Microfluidics in Detection Science : Lab-on-a-chip Technologies, Royal Society of Chemistry, 2014

Références

↑ ^{a b et c} (en) Frieder Mugele, « Fundamental challenges in electrowetting: from equilibrium shapes to contact angle saturation and drop dynamics », Soft Matter, Royal Society of Chemistry, n^o 5,‎ 2009, p. 3377–3384 (DOI 10.1039/B904493K)
↑ (en) Edward Bormashenko et Oleg Gendelman, « A generalized electrowetting equation: Its derivation and consequences », Chemical Physics Letters, vol. 599,‎ 2014, p. 139–141 (ISSN 0009-2614, DOI 10.1016/j.cplett.2014.03.032, arXiv 1511.01704)
↑ ^{a et b} (en) Wyatt C. Nelson et Chang-Jin ‘CJ’ Kim, « Droplet Actuation by Electrowetting-on-Dielectric (EWOD): A Review », Journal of Adhesion Science and Technology, vol. ahead-of-print, n^o ahead-of-print,‎ 2012, p. 1–25 (ISSN 0169-4243, DOI 10.1163/156856111X599562, lire en ligne, consulté le 8 février 2017)
↑ ^{a et b} (en) Philip Day, Andreas Manz et Yonghao Zhang, Microdroplet Technology : Principles and Emerging Applications in Biology and Chemistry, New York, Springer Science & Business Media, 2012, 246 p. (ISBN 978-1-4614-3265-4, lire en ligne)
↑ Malk 2011, p. 42
↑ Malk 2011, p. 43
↑ (en) Christopher B. Gorman, Hans A. Biebuyck et George M. Whitesides, « Control of the Shape of Liquid Lenses on a Modified Gold Surface Using an Applied Electrical Potential across a Self-Assembled Monolayer », Langmuir, vol. 11, n^o 6,‎ 1995, p. 2242–2246 (ISSN 0743-7463, DOI 10.1021/la00006a063, lire en ligne, consulté le 8 février 2017)
↑ ^{a b et c} (en) T. B. Jones et K.-L. Wang, « Frequency-Dependent Electromechanics of Aqueous Liquids: Electrowetting and Dielectrophoresis », Langmuir, vol. 20,‎ 2004, p. 2813-2818
↑ Labeed 2014, p. 95
↑ ^{a et b} (en) Florian Lapierre, Martin Jonsson-Niedziolka, Yannick Coffinier, Rabah Boukherroub et Vincent Thomy, « Droplet transport by electrowetting: lets get rough! », Microfluidics and Nanofluidics, vol. 15, n^o 3,‎ 2013, p. 327–336 (ISSN 1613-4982, DOI 10.1007/s10404-013-1149-1)
↑ (en) Mun Nahar, Jagath Nikapitiya, Seung You et Hyejin Moon, « Droplet Velocity in an Electrowetting on Dielectric Digital Microfluidic Device », Micromachines, vol. 7, n^o 4,‎ 2016, p. 71 (ISSN 2072-666X, DOI 10.3390/mi7040071)
↑ ^{a et b} (en) Chonglei Hao, « DElectrowetting on liquid-infused film (EWOLF): Complete reversibility and controlled droplet oscillation suppression for fast optical imaging », Scientific Reports, vol. 4, n^o 6846,‎ 2014, p. 71 (ISSN 2072-666X, DOI 10.3390/mi7040071)
↑ ^{a et b} (en) Tom Krupenkin et J. Ashley Taylor, « Reverse electrowetting as a new approach to high-power energy harvesting », Nature Communications, vol. 2, n^o 2,‎ 2011 (DOI 10.1038/ncomms1454, lire en ligne, consulté le 14 juillet 2017)
↑ (en) Kazimierz Adamiak, « Capillary and electrostatic limitations to the contact angle in electrowetting-on-dielectric », Microfluid Nanofluid, vol. 2, n^o 6,‎ novembre 2006, p. 471–480 (DOI 10.1007/s10404-006-0090-y)
↑ Malk 2011, p. 54
↑ (en) Jin Seok Hong et Al, « A numerical investigation on AC electrowetting of a droplet », Microfluid Nanofluid, vol. 5,‎ 2008, p. 263–271
↑ ^{a b et c} (en) Frieder Mugele et Jean-Christophe Baret, « Electrowetting: from basics to applications », Journal of Physics: Condensed Matter, vol. 17, n^o 28,‎ 2005, p. 705-774
↑ Malk 2011, p. 53
↑ (en) Anthony Quinn et al., « Contact Angle Saturation in Electrowetting », J. Phys. Chem. B, vol. 109, n^o 13,‎ 11 mars 2005, p. 6268–6275 (DOI 10.1021/jp040478f)
↑ (en) Anthony Quinn et al., « Repulsion-based model for contact angle saturation in electrowetting », Biomicrofluidics, vol. 9, n^o 1,‎ février 2015, p. 014115 (DOI 10.1063/1.4907977)
↑ ^{a et b} (en) Shih-Kang Fan et Al, « Asymmetric electrowetting—moving droplets by a square wave », Applied Physics Letters, vol. 86,‎ 2005, p. 1330-1335 (DOI 10.1039/B704084A)
↑ (en) A. G. Papathanasiou et A. G. Boudouvis, « Manifestation of the connection between dielectric breakdown strength and contact angle saturation in electrowetting », Lab On Chip, vol. 7,‎ 2007, p. 1330-1335 (DOI 10.1063/1.1905809)
↑ ^{a et b} (en) Li et Mugele, « How to make sticky surfaces slippery: Contact angle hysteresis in electrowetting with alternating voltage », Applied Physics Letters, vol. 92,‎ 2008 (DOI 10.1063/1.2945803)
↑ (en) Rohini Gupta, Danica M. Sheth, Teno K. Boone, Arianne B. Sevilla et Joëlle Fréchette, « Impact of Pinning of the Triple Contact Line on Electrowetting Performance », Langmuir, vol. 27, n^o 24,‎ 2011, p. 14923–14929 (ISSN 0743-7463, DOI 10.1021/la203320g)
↑ (en) Pei Yu Chiou, « Light actuation of liquid by optoelectrowetting », Sensors and Actuators A: Physical, vol. 104, n^o 3,‎ 2003, p. 222-228 (DOI 10.1016/S0924-4247(03)00024-4)
↑ (en) Arscott S, « Moving liquids with light: photoelectrowetting on semiconductors », Scientific Reports, vol. 1, n^o 1,‎ 2011 (DOI doi:10.1038/srep00184)
↑ (en) B. Roman et J. Bico, « Elasto-capillarity: deforming an elastic structure with a liquid droplet », J. Phys.: Condens. Matter, vol. 22, n^o 49,‎ 2010 (lire en ligne, consulté le 10 juillet 2017)
↑ (en) Jean Berthier, Micro-Drops and Digital Microfluidics, Amsterdam, William Andrew, 2013, 560 p. (ISBN 978-1-4557-2550-2), Ch.12
↑ (en) SamanSeifi et Harold S.Park, « Computational modeling of electro-elasto-capillary phenomena in dielectric elastomers », International Journal of Solids and Structures, vol. 87, n^o 49,‎ 2016, p. 236-244 (lire en ligne, consulté le 10 juillet 2017)
↑ (en) Ziquian Wang, « Tap dance of a water droplet », Proc. R. Soc. A, vol. 468,‎ 2012, p. 2485–2495 (DOI 10.1098/rspa.2011.0679, lire en ligne, consulté le 10 juillet 2017)
↑ Gabriel Lippmann, « Relations entre les phénomènes électriques et capillaires »
↑ Gabriel Lippmann, « Relation entre les phénomènes électriques et capillaires », Ann. Chim. Phys, n^o 5,‎ 1875, p. 494 (lire en ligne)
↑ Théodore du Moncel et Bonnafoux, Le Téléphone, le Microphone et le Phonographe, Paris, Hachette, 1878
↑ (en) Catherine Quilliet et Bruno Berge, « Electrowetting: a recent outbreak », Current Opinion in Colloid & Interface Science, vol. 6, n^o 1,‎ 2001, p. 35-39
↑ (en) Gerardo Beni et Susan Hackwood, « Electro‐wetting displays », Applied Physics Letters, vol. 38, n^o 4,‎ février 1981, p. 207-209 (DOI 10.1063/1.92322)
↑ Bulletin signalétique des télécommunications, Volume 37, 1982
↑ (en) B. Berge and J. Peseux, « Variable focal lens controlled by an external voltage: an application of electrowetting », The European Physical Journal, vol. 3,‎ 2000, p. 159-163
↑ « Des optiques qui focalisent sans bouger », sur usinenouvelle.com/, 5 mars 2012 (consulté le 11 février 2017)
↑ Malk 20111, p. 20
↑ (en) H. You et A.J. Steck, « Three-color electrowetting display device for electronic paper », Applied physics letters, vol. 97,‎ 2010, p. 023514 (DOI 10.1063/1.3464963)
↑ « Amazon rachète les écrans Liquavista à Samsung – CNET France », sur CNET France, 29 août 2017 (consulté le 29 août 2017)
↑ (en) Neil R. Smith, Don C. Abeysinghe, Joseph W. Haus et Jason Heikenfeld, « Agile wide-angle beam steering with electrowetting microprisms », Soft Matter, Royal Society of Chemistry, vol. 14, n^o 14,‎ 2009, p. 6557–6563 (DOI 10.1364/OE.14.006557, lire en ligne, consulté le 19 juillet 2017)
↑ (en) L Hou, J Zhang, N Smith et Jason Heikenfeld, « A full description of a scalable microfabrication process for arrayed electrowetting microprisms », J. Micromech. Microeng, vol. 20,‎ 2009, p. 6557–6563 (DOI 10.1088/0960-1317/20/1/015044)
↑ (en) Kevin Ylli et al., « Energy harvesting from human motion:exploiting swing and shock excitations », Smart Materials and Structures, vol. 24, n^o 2,‎ 14 janvier 2014 (DOI 10.1088/0964-1726/24/2/025029)

Cet article est reconnu comme « bon article » depuis sa version du 12 septembre 2017 (comparer avec la version actuelle).
Pour toute information complémentaire, consulter sa page de discussion et le vote l'ayant promu.

La version du 12 septembre 2017 de cet article a été reconnue comme « bon article », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.

[Mugele2-1] {a b et c} (en) Frieder Mugele, « Fundamental challenges in electrowetting: from equilibrium shapes to contact angle saturation and drop dynamics », Soft Matter, Royal Society of Chemistry, n^o 5,‎ 2009, p. 3377–3384 (DOI 10.1039/B904493K)

[Borma-2] (en) Edward Bormashenko et Oleg Gendelman, « A generalized electrowetting equation: Its derivation and consequences », Chemical Physics Letters, vol. 599,‎ 2014, p. 139–141 (ISSN 0009-2614, DOI 10.1016/j.cplett.2014.03.032, arXiv 1511.01704)

[Nelson-3] {a et b} (en) Wyatt C. Nelson et Chang-Jin ‘CJ’ Kim, « Droplet Actuation by Electrowetting-on-Dielectric (EWOD): A Review », Journal of Adhesion Science and Technology, vol. ahead-of-print, n^o ahead-of-print,‎ 2012, p. 1–25 (ISSN 0169-4243, DOI 10.1163/156856111X599562, lire en ligne, consulté le 8 février 2017)

[Day-4] {a et b} (en) Philip Day, Andreas Manz et Yonghao Zhang, Microdroplet Technology : Principles and Emerging Applications in Biology and Chemistry, New York, Springer Science & Business Media, 2012, 246 p. (ISBN 978-1-4614-3265-4, lire en ligne)

[5] Malk 2011, p. 42

[6] Malk 2011, p. 43

[gorman-7] (en) Christopher B. Gorman, Hans A. Biebuyck et George M. Whitesides, « Control of the Shape of Liquid Lenses on a Modified Gold Surface Using an Applied Electrical Potential across a Self-Assembled Monolayer », Langmuir, vol. 11, n^o 6,‎ 1995, p. 2242–2246 (ISSN 0743-7463, DOI 10.1021/la00006a063, lire en ligne, consulté le 8 février 2017)

[jones-8] {a b et c} (en) T. B. Jones et K.-L. Wang, « Frequency-Dependent Electromechanics of Aqueous Liquids: Electrowetting and Dielectrophoresis », Langmuir, vol. 20,‎ 2004, p. 2813-2818

[9] Labeed 2014, p. 95

[Lapierre-10] {a et b} (en) Florian Lapierre, Martin Jonsson-Niedziolka, Yannick Coffinier, Rabah Boukherroub et Vincent Thomy, « Droplet transport by electrowetting: lets get rough! », Microfluidics and Nanofluidics, vol. 15, n^o 3,‎ 2013, p. 327–336 (ISSN 1613-4982, DOI 10.1007/s10404-013-1149-1)

[Nahar-11] (en) Mun Nahar, Jagath Nikapitiya, Seung You et Hyejin Moon, « Droplet Velocity in an Electrowetting on Dielectric Digital Microfluidic Device », Micromachines, vol. 7, n^o 4,‎ 2016, p. 71 (ISSN 2072-666X, DOI 10.3390/mi7040071)

[Chonglei-12] {a et b} (en) Chonglei Hao, « DElectrowetting on liquid-infused film (EWOLF): Complete reversibility and controlled droplet oscillation suppression for fast optical imaging », Scientific Reports, vol. 4, n^o 6846,‎ 2014, p. 71 (ISSN 2072-666X, DOI 10.3390/mi7040071)

[Krutay-13] {a et b} (en) Tom Krupenkin et J. Ashley Taylor, « Reverse electrowetting as a new approach to high-power energy harvesting », Nature Communications, vol. 2, n^o 2,‎ 2011 (DOI 10.1038/ncomms1454, lire en ligne, consulté le 14 juillet 2017)

[Adamiak-14] (en) Kazimierz Adamiak, « Capillary and electrostatic limitations to the contact angle in electrowetting-on-dielectric », Microfluid Nanofluid, vol. 2, n^o 6,‎ novembre 2006, p. 471–480 (DOI 10.1007/s10404-006-0090-y)

[15] Malk 2011, p. 54

[Hong-16] (en) Jin Seok Hong et Al, « A numerical investigation on AC electrowetting of a droplet », Microfluid Nanofluid, vol. 5,‎ 2008, p. 263–271

[Mugele-17] {a b et c} (en) Frieder Mugele et Jean-Christophe Baret, « Electrowetting: from basics to applications », Journal of Physics: Condensed Matter, vol. 17, n^o 28,‎ 2005, p. 705-774

[18] Malk 2011, p. 53

[Contact_Quinn-19] (en) Anthony Quinn et al., « Contact Angle Saturation in Electrowetting », J. Phys. Chem. B, vol. 109, n^o 13,‎ 11 mars 2005, p. 6268–6275 (DOI 10.1021/jp040478f)

[Ali-20] (en) Anthony Quinn et al., « Repulsion-based model for contact angle saturation in electrowetting », Biomicrofluidics, vol. 9, n^o 1,‎ février 2015, p. 014115 (DOI 10.1063/1.4907977)

[Shih-Kang-21] {a et b} (en) Shih-Kang Fan et Al, « Asymmetric electrowetting—moving droplets by a square wave », Applied Physics Letters, vol. 86,‎ 2005, p. 1330-1335 (DOI 10.1039/B704084A)

[Papat-22] (en) A. G. Papathanasiou et A. G. Boudouvis, « Manifestation of the connection between dielectric breakdown strength and contact angle saturation in electrowetting », Lab On Chip, vol. 7,‎ 2007, p. 1330-1335 (DOI 10.1063/1.1905809)

[sticky-23] {a et b} (en) Li et Mugele, « How to make sticky surfaces slippery: Contact angle hysteresis in electrowetting with alternating voltage », Applied Physics Letters, vol. 92,‎ 2008 (DOI 10.1063/1.2945803)

[gupta1-24] (en) Rohini Gupta, Danica M. Sheth, Teno K. Boone, Arianne B. Sevilla et Joëlle Fréchette, « Impact of Pinning of the Triple Contact Line on Electrowetting Performance », Langmuir, vol. 27, n^o 24,‎ 2011, p. 14923–14929 (ISSN 0743-7463, DOI 10.1021/la203320g)

[Chiou-25] (en) Pei Yu Chiou, « Light actuation of liquid by optoelectrowetting », Sensors and Actuators A: Physical, vol. 104, n^o 3,‎ 2003, p. 222-228 (DOI 10.1016/S0924-4247(03)00024-4)

[Arscott-26] (en) Arscott S, « Moving liquids with light: photoelectrowetting on semiconductors », Scientific Reports, vol. 1, n^o 1,‎ 2011 (DOI doi:10.1038/srep00184)

[Roman-27] (en) B. Roman et J. Bico, « Elasto-capillarity: deforming an elastic structure with a liquid droplet », J. Phys.: Condens. Matter, vol. 22, n^o 49,‎ 2010 (lire en ligne, consulté le 10 juillet 2017)

[Berthier-28] (en) Jean Berthier, Micro-Drops and Digital Microfluidics, Amsterdam, William Andrew, 2013, 560 p. (ISBN 978-1-4557-2550-2), Ch.12

[Seifi-29] (en) SamanSeifi et Harold S.Park, « Computational modeling of electro-elasto-capillary phenomena in dielectric elastomers », International Journal of Solids and Structures, vol. 87, n^o 49,‎ 2016, p. 236-244 (lire en ligne, consulté le 10 juillet 2017)

[wang-30] (en) Ziquian Wang, « Tap dance of a water droplet », Proc. R. Soc. A, vol. 468,‎ 2012, p. 2485–2495 (DOI 10.1098/rspa.2011.0679, lire en ligne, consulté le 10 juillet 2017)

[lippmann-31] Gabriel Lippmann, « Relations entre les phénomènes électriques et capillaires »

[32] Gabriel Lippmann, « Relation entre les phénomènes électriques et capillaires », Ann. Chim. Phys, n^o 5,‎ 1875, p. 494 (lire en ligne)

[Moncel-33] Théodore du Moncel et Bonnafoux, Le Téléphone, le Microphone et le Phonographe, Paris, Hachette, 1878

[Quilliet-34] (en) Catherine Quilliet et Bruno Berge, « Electrowetting: a recent outbreak », Current Opinion in Colloid & Interface Science, vol. 6, n^o 1,‎ 2001, p. 35-39

[Beni-35] (en) Gerardo Beni et Susan Hackwood, « Electro‐wetting displays », Applied Physics Letters, vol. 38, n^o 4,‎ février 1981, p. 207-209 (DOI 10.1063/1.92322)

[36] Bulletin signalétique des télécommunications, Volume 37, 1982

[Peseux-37] (en) B. Berge and J. Peseux, « Variable focal lens controlled by an external voltage: an application of electrowetting », The European Physical Journal, vol. 3,‎ 2000, p. 159-163

[usinen-38] « Des optiques qui focalisent sans bouger », sur usinenouvelle.com/, 5 mars 2012 (consulté le 11 février 2017)

[39] Malk 20111, p. 20

[Steck-40] (en) H. You et A.J. Steck, « Three-color electrowetting display device for electronic paper », Applied physics letters, vol. 97,‎ 2010, p. 023514 (DOI 10.1063/1.3464963)

[41] « Amazon rachète les écrans Liquavista à Samsung – CNET France », sur CNET France, 29 août 2017 (consulté le 29 août 2017)

[Smith-42] (en) Neil R. Smith, Don C. Abeysinghe, Joseph W. Haus et Jason Heikenfeld, « Agile wide-angle beam steering with electrowetting microprisms », Soft Matter, Royal Society of Chemistry, vol. 14, n^o 14,‎ 2009, p. 6557–6563 (DOI 10.1364/OE.14.006557, lire en ligne, consulté le 19 juillet 2017)

[Hou-43] (en) L Hou, J Zhang, N Smith et Jason Heikenfeld, « A full description of a scalable microfabrication process for arrayed electrowetting microprisms », J. Micromech. Microeng, vol. 20,‎ 2009, p. 6557–6563 (DOI 10.1088/0960-1317/20/1/015044)

[Ylli2-44] (en) Kevin Ylli et al., « Energy harvesting from human motion:exploiting swing and shock excitations », Smart Materials and Structures, vol. 24, n^o 2,‎ 14 janvier 2014 (DOI 10.1088/0964-1726/24/2/025029)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]