Groupe de Grigorchuk

En mathématiques et notamment en théorie des groupes, le groupe de Grigorchuk, aussi appelé le premier groupe de Grigorchuk, est un groupe finiment engendré construit par Rostislav Grigorchuk et qui fournit le premier exemple d'un groupe finiment engendré de croissance intermédiaire, c'est-à-dire plus rapide qu'un polynôme et plus lent qu'une exponentielle. Le groupe de Grigorchuk est aussi le premier exemple d'un groupe moyennable qui n’est pas élémentairement moyennable, ce qui répond à une question de Mahlon Day posée en 1957.

Historique

Le groupe a été construit par Grigorchuk en 1980, et il a prouvé qu'il est de croissance intermédiaire en 1984 ; ceci répond à une question posée par John Milnor en 1968. Le groupe de Grigorchuk continue à être un objet clé en théorie géométrique des groupes, en particulier en relation avec les groupes automatiques, et a aussi des connexions avec les groupes de monodromie itérée.

Le taux de croissance d'un groupe finiment engendré est le nombre b(n) d'éléments du groupe qui sont produits d'au plus n éléments de l'ensemble de générateurs. Grigorchuk a prouvé que b(n) croît plus vite que $\exp({\sqrt {n}})$ mais moins vite que $\exp(n^{s})$ où $s=\log _{32}31\approx 0.991$.

La borne supérieure a été améliorée par Laurent Bartholdi qui obtient :

$s={\frac {\log 2}{\log 2-\log \eta }}\approx 0.7675$,

où $\eta$ vérifie $\eta ^{3}+\eta ^{2}+\eta =2.$ Une meilleure borne inférieure $\exp(n^{0.504})$ a été démontrée par Yurii Leonov.

Un résultat lié est le théorème de Gromov sur les groupes à croissance polynomiale, obtenu par Mikhaïl Gromov en 1981, qui montre qu'un groupe finiment engendré a croissance polynomiale si et seulement si ce groupe a un sous-groupe nilpotent d'index fini. Avant l'exemple de Grigorchuk, plusieurs résultats ont décrit des classes de groupes dont la croissance est soit polynomiale soit exponentielle, comme les groupes linéaires ou les groupes résolubles etc.

Des extensions et généralisations ont été proposées par divers auteurs.

Construction

Arbre binaire $T_{2}$.

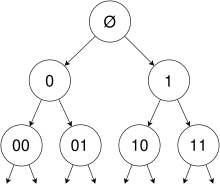
Le groupe de Grigorchuk est défini comme un groupe d'automorphismes de l’arbre binaire infini. L'arbre, noté $T$ (on rencontre aussi la notation $T^{(2)}$ ou $T_{2}$), est vu comme l'ensemble $\Sigma ^{*}$ des mots finis sur l'alphabet $\Sigma =\{0,1\}$, y compris le mot vide $\varepsilon$ (ou $\varnothing$) qui est la racine de l’arbre. Pour tout nœud $x$ de l’arbre $T$, le mot $x0$ est le fils gauche de $x$ et le mot $x1$ est le fils droit de $x$ dans $T$. Le groupe ${\text{Aut}}(T)$ peut alors être vu comme le groupe de toutes les bijections $\sigma$ de $\Sigma ^{*}$ qui préservent les longueurs, donc qui sont des permutations sur les mots de même longueur, et qui respectent les préfixes ; en d'autres termes, si $y$ est préfixe de $x$, alors $\sigma (y)$ est préfixe de $\sigma (x)$.

Le groupe de Grigorchuk $G$ est le sous-groupe du groupe d'automorphisme ${\text{Aut}}(T)$ engendré par quatre éléments particuliers de ${\text{Aut}}(T)$, notés $a,b,c,d$, soit

$G=\langle a,b,c,d\rangle$,

où les automorphismes $a,b,c,d$ sont définis par les relations suivantes :

${\begin{aligned}&a(0x)=1x\\&a(1x)=0x\\\end{aligned}}\qquad {\begin{aligned}&b(0x)=0a(x)\\&b(1x)=1c(x)\\\end{aligned}}\qquad {\begin{aligned}&c(0x)=0a(x)\\&c(1x)=1d(x)\\\end{aligned}}\qquad {\begin{aligned}&d(0x)=0x\\&d(1x)=1b(x).\\\end{aligned}}$

Dans ces formules, $x$ est un mot de $\Sigma ^{*}$, y compris le mot vide. Pour $x=\varepsilon$, les formules se réduisent à

$a(0)=1,\ a(1)=0,\ b(0)=c(0)=d(0)=0,\ b(1)=c(1)=d(1)=1,$

puisque l'image du mot vide par un automorphisme est toujours le mot vide. Seule l'automorphisme $a$ est défini explicitement, les autres le sont par récurrence sur la longueur de l'argument, qui correspond à la hauteur de l'élément dans l'arbre. Par exemple, l'évaluation de $b(1011)$ donne

$b(1011)=1c(011)=10a(11)=1001$.

L'ensemble des mots de $\Sigma ^{*}$ s'écrit comme réunion disjointe

$\Sigma ^{*}=\{\varepsilon \}\cup 0\Sigma ^{*}\cup 1\Sigma ^{*}$.

Les sommets de $T$ dénotés par $0\Sigma ^{*}$ et $1\Sigma ^{*}$ constituent respectivement le sous-arbre gauche et le sous-arbre droit de $T$, notés $T_{L}$ (parfois aussi $T_{0}$) et $T_{R}$ (ou $T_{1}$). On a alors

$a(T_{L})=T_{R},\quad a(T_{R})=T_{L}$,

en d'autres termes $a$ échange les éléments des sous-arbres gauche et droit niveau par niveau. Les actions de $b,c$ et $d$ peuvent s'écrire aussi sous la forme :

$b=(a,c)\quad c=(a,d)\quad d=(e,b)$

où $e$ est l'identité du groupe d'automorphisme, et où la première composante est l’action quand le mot est dans le sous-arbre gauche, la deuxième composante quand est dans le sous-arbre droit ; en d'autres termes :

$b(x)={\begin{cases}a(x)&x\in T_{L}\\c(x)&x\in T_{R}\end{cases}}\quad c(x)={\begin{cases}a(x)&x\in T_{L}\\d(x)&x\in T_{R}\end{cases}}\quad d(x)={\begin{cases}x&x\in T_{L}\\b(x)&x\in T_{R}\end{cases}}$.

Relations

Plusieurs formules relient les éléments. Notamment la conjugaison par $a$ permet l'échange des composants :

$aba=(c,a),\quad aca=(d,a),\quad ada=(b,e).$

La vérification est facile, ainsi

$aba(0x)=ab(1x)=a(1c(x))=0c(x),\ aba(1x)=ab(0x)=a(0a(x))=1a(x)$.

Les éléments $a,b,c$, et $d$ sont des involutions ; la preuve est directe pour $a$, et par récurrence sur la longueur des mots pour les autres :

${\begin{aligned}&a(a(0x))=a(1x)=0x,&&a(a(1x))=a(0x)=1x\\&b(b(0x))=b(0a(x))=0a^{2}(x)=0x,&&b(b(1x))=b(1c(x))=1c^{2}(x)\\&c(c(0x))=c(0a(x))=0a^{2}(x)=0x,&&c(c(1x))=c(1d(x))=1d^{2}(x)\\&d(d(0x))=d(0x)=0x,&&d(d(1x))=d(1b(x))=1b^{2}(x).\\\end{aligned}}$

Les éléments $b,c,d$ commutent deux-à-deux et leur produit est égal au troisième :

$bc=cb=d,\ bd=db=c,\ dc=cd=b.$

de sorte que $\langle b,c,d\rangle$ est un groupe abélien d'ordre 4 isomorphe au produit direct de deux groupes cycliques d'ordre 2.

Il en résulte aussi que le groupe $G$ est aussi engendré par trois éléments, à savoir $a$ et deux quelconques parmi $b,c,d$. Ainsi, $G=\langle a,b,c\rangle =\langle a,b,d\rangle =\langle a,c,d\rangle$.

Mot réduit : Tout élément de $G$ s'écrit comme produit d'éléments de sorte qu'entre deux $a$, il y a exactement un des éléments b, c, ou d. Une telle écriture est dite réduite. Ainsi, l'écriture réduite de $x=ab^{3}cda^{2}cdab$ est $r(ab^{3}cda^{2}cdab)=abab$.

Propriétés

Voici des propriétés de base du groupe de Grigorchuk (des démonstrations sont données dans la monographie de Pierre de la Harpe):

• Le groupe $G$ est infini.
• Le groupe $G$ est résiduellement fini. Soit $\rho _{n}:G\to {\text{Aut}}(T[n])$ le morphisme qui envoie un élément de $G$ sur sa restriction à l'arbre fini $T[n]$ de hauteur $n$. Les groupes ${\text{Aut}}(T[n])$ sont finis et pour tout $g\in G$ non trivial, il existe un $n$ tel que $\rho _{n}(g)\neq 1$.
• Le groupe $G$ est un 2-groupe, c'est-à-dire tous ses éléments sont d'ordre fini qui de plus est une puissance de 2.
• Le groupe $G$ est de croissance intermédiaire.
• Le groupe $G$ est moyennable mais n'est pas un groupe élémentairement moyennable (en).
• Le groupe $G$ est juste infini (en), c'est-à-dire qu'il est infini mais que tous ses groupes quotient sont finis.
• Le groupe $G$ a la congruence subgroup property : un sous-groupe H est d'indice fini dans G si et seulement si $\ker(\rho _{n})\leqslant H.$ pour un entier n.
• Le problème de l’appartenance à un sous-groupe est décidable dans le groupe G ; en d'autres termes, il existe un algorithme qui, étant donné des mots $w,u_{1},\ldots ,u_{n}$, décide si $w$ est un élément du sous-groupe engendré par $u_{1},\ldots ,u_{n}$.
• Le groupe $G$ est séparable (en), c'est-à-dire tout sous-groupe finiment engendré est fermé dans la topologie profinie sur $G$
• Tout sous-groupe maximal de $G$ est d'indice fini dans $G$.
• Le groupe $G$ est finiment engendré mais n’a pas de présentation finie.

Décidabilité

• Le stabilisateur des sommets de niveau 1 de $T$ dans G (le sous-groupe des éléments qui opèrent comme identité sur 0 and 1), est le groupe :

$G_{\{0,1\}}=\langle b,c,d,aba,aca,ada\rangle .$

$G_{\{0,1\}}$ est un sous-groupe normal d'index 2 dans G et

$G=G_{\{0,1\}}\sqcup aG_{\{0,1\}}.$

• Un mot réduit représente un élément de $G_{\{0,1\}}$ si et seulement s'il contient un nombre pair d'occurrences de a.
• Si w est un mot réduit de G avec un nombre pair positif d'occurrences de a, alors il existe des mots u, v pas nécessairement réduits tels que :

$w=(u,v)\quad$ et $\quad {\begin{cases}|u|,|v|\leqslant {\tfrac {1}{2}}|w|&|w|{\text{ impair}}\\|u|,|v|\leqslant {\tfrac {1}{2}}(|w|+1)&|w|{\text{ pair}}\end{cases}}$

Ceci est parfois appelé la propriété de contraction. Elle joue un rôle majeur dans de nombreuses démonstrations car elle permet d'opérer par récurrence sur la longueur des mots.

• Le problème des mots et le problème de conjugaison sont décidables pour le groupe $G$. Ceci s'obtient comme conséquence de la propriété de contraction.

Automates

Automate de Mealy du groupe de Grigorchuk

L'usage d'automates finis, et notamment d'automates de Mealy, pour la représentation et l’étude du groupe Grigorchuk s'est révélée utile. Les automates considérés n'ont pas d'états initiaux ni terminaux. Les états sont en bijection avec les générateurs du groupe, augmentés de l'automorphisme identité, et les transitions sont les quadruplets $(p,i,j,q)$ tels que $p(ix)=jq(x)$, où $i,j\in \{0,1\}$ et $p,q\in \{a,b,c,d,e\}$. On voit qu'il existe un chemin de $p$ à $q$ d'étiquette d'entrée $y$ et d'étiquette de sortie $z$ si et seulement si $p(yx)=zq(x)$. Par exemple, il y a dans l’automate le chemin

$b\,{\xrightarrow {1|1}}\,c\,{\xrightarrow {0|0}}\,a\,{\xrightarrow {1|0}}\,e\,{\xrightarrow {1|1}}\,e$

représentant le calcul

$b(1011)=1c(011)=10a(11)=1001$.

L'étude des automates de Mealy et des groupes et demi-groupes de transformations qu'ils définissent a été développée par Laurent Bartholdi ou Thibault Godin, Inès Klimann, Matthieu Picantin.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Grigorchuk group » (voir la liste des auteurs).

Bibliographie

• Laurent Bartholdi, « Decidability problems in automaton semigroups », preprint,‎ 2017 (arXiv 1705.04598v1)
• Laurent Bartholdi, « The growth of Grigorchuk's torsion group », International Mathematics Research Notices, Oxford Academic, n^o 20,‎ 1998, p. 1049-1054 (DOI 10.1155/S1073792898000622, arXiv math/0012108v1).
• (en) L. Bartholdi, I.I. Reznykov et V.I. Sushchansky, « The smallest Mealy automaton of intermediate growth », Journal of Algebra, vol. 295, n^o 2,‎ 2006, p. 387–414 (ISSN 0021-8693, DOI 10.1016/j.jalgebra.2004.08.040, arXiv math/0407312v1)
• Tullio Ceccherini-Silberstein, Antonio Machì et Fabio Scarabotti, « The Grigorchuk group of intermediate growth », Rendiconti del Circolo Matematico di Palermo (2), vol. 50, n^o 1,‎ 2001, p. 67-102
• Thibault Godin, Ines Klimann et Matthieu Picantin, « On torsion-free semigroups generated by invertible reversible Mealy automata », LATA 2015, Springer,‎ 2015, p. 328–339 (DOI 10.1007/978-3-319-15579-1_25, MR 3344813, arXiv abs/1410.4488)
• Rostislav I. Grigorchuk et Igor Pak, « Groups of intermediate growth: an introduction », L´Enseignement Mathématique, vol. 54,‎ 2008, p. 251-272 (arXiv math/0607384, lire en ligne)
• Rostislav I. Grigorchuk, « Complete growth functions of hyperbolic groups », Invent. Math., vol. 130, n^o 1,‎ 1997, p. 159–188.
• Rostislav I. Grigorchuk, « On growth in group theory », Proceedings of the International Congress of Mathematicians, Kyoto, Math. Soc. Japon, vol. I, II (Kyoto, 1990),‎ 1991, p. 325–338.
• Rostislav I. Grigorchuk, « Degrees of growth of finitely generated groups and the theory of invariant means. », Izv. Akad. Nauk SSSR Ser. Mat., vol. 48, n^o 5,‎ 1984, p. 939–985.
• Rostislav I. Grigorchuk, « On the Milnor problem of group growth », Dokl. Akad. Nauk SSSR, vol. 271, n^o 1,‎ 1983, p. 30–33.
• Rostislav I. Grigorchuk, « On Burnside's problem on periodic groups », Funktsional. Anal. i Prilozheniya, vol. 14, n^o 1,‎ 1980, p. 53–54 (MR 0565099).
• Rostislav I. Grigorchuk et J. S. Wilson, « A structural property concerning abstract commensurability of subgroups », Journal of the London Mathematical Society (2), vol. 68, n^o 3,‎ 2003, p. 671–682 (lire en ligne).
• (en) Pierre de la Harpe, Topics in geometric group theory, Chicago, University of Chicago Press, coll. « Chicago Lectures in Mathematics », 2000, 310 p. (ISBN 0-226-31719-6, lire en ligne)
• I. G. Lysenok, « A set of defining relations for the Grigorchuk group », Mathematical Notes of the Academy of Sciences of the USSR, vol. 38, n^o 4,‎ 1985, p. 784–792 (DOI 10.1007/BF01158402).
• (ru) Yu. G. Leonov, « On a lower bound for the growth function of the Grigorchuk group », Matematicheskie Zametki, vol. 67, n^o 3,‎ 2000, p. 475-477 — Traduction dans Mathematical Notes, vol. 67, n^o 3-4 (2000) p. 403-405.
• (ru) Ekaterina L. Pervova, « Everywhere dense subgroups of a group of tree automorphisms », Trudy Matematicheskogo Instituta Imeni V. A. Steklova, vol. 231,‎ 2000, p. 356–367 — Traduction : Proceedings of the Steklov Institute of Mathematics, vol. 231, n^o 4, 2000, p. 339–350.
• Roman Muchnik et Igor Pak, « Percolation on Grigorchuk groups », Communications in Algebra, vol. 29, n^o 2,‎ 2001, p. 661-671.

Articles liés

• Théorie géométrique des groupes
• Growth rate of finitely generated groups
• Groupe moyennable
• Monodromie
• Automate de Mealy
• Groupe d'allumeur de réverbères