Onde inertielle
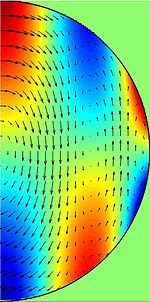
Les ondes inertielles ou oscillations inertielles sont un type d'ondes mécaniques qu'on retrouve dans un fluide en rotation. Contrairement aux vagues qui animent la surface, les ondes inertielles affectent la masse du fluide. Elles résultent de la tendance de retour à l'état initial des mouvements induits par une force d'inertie. La force le plus souvent à l'origine de ces ondes est celle de Coriolis, ce qui lui donne une longueur d'onde et une fréquence ayant certaines valeurs particulières. Les ondes inertielles les plus connues sont les ondes de Rossby, les vents et courants géostrophiques dans l'atmosphère. On les retrouve également dans les océans et dans le magma.
Les ondes inertielles sont responsables des variations à grande échelle du mouvement des fluides, ce qui mène aux mélanges entre parties de différentes densités ou compositions, par exemple au mélange des masses d'air de l'atmosphère ou des zones de différentes salinités de l'océan. Ces mélanges se font souvent en régime turbulent pour lequel un traitement mathématique rigoureux est possible dans la limite d'une rotation rapide.
Force de réaction[modifier | modifier le code]
Pour comprendre l'idée d'une force de réaction, pensons à une corde de guitare tendue et qu'on déplace vers le bas. L'élasticité de la corde la fait revenir en lui donnant une accélération proportionnelle à la distance au point initial. Elle acquiert ainsi une vitesse qui la fait dépasser ce dernier, puis elle subit une force de décélération qui la ralentit graduellement pour atteindre une distance maximale de l'autre côté de l'équilibre ; puis le processus se répète dans la direction inverse. Sans friction, cet effet de pendule continuerait indéfiniment, mais en réalité la vibration va s'arrêter à cause de celle-ci.
Dans un fluide, l'équilibre se produit quand il est parfaitement au repos et donc que sa surface est uniforme. Lorsqu'une perturbation augmente ou baisse le niveau en un point, la gravité va s'exercer pour retourner la surface à l'équilibre et induire une onde dite onde de gravité.
Dans le cas d'une onde inertielle, le fluide étant en rotation, l'état d'équilibre est qu'il tourne toujours à la même distance de l'axe de rotation. Par exemple, dans le cas de l'atmosphère, l'état d'équilibre est réalisé lorsque l'air à une latitude donnée accompagne la rotation de la Terre toujours le long de celle-ci. La parcelle de fluide en rotation a donc un moment de rotation qui dépend de cette latitude par le facteur de Coriolis. Si on la change de latitude, la grandeur de cette force change et la force de Coriolis, agissant à 90 degrés de la direction de mouvement, la ramène vers son point d'équilibre. Sa force est également proportionnelle au taux de rotation selon la latitude. Ces deux caractéristiques donnent une formulation de la balance des forces dans ce mouvement qui est peu intuitive.
Description mathématique[modifier | modifier le code]
Un fluide en rotation obéit aux équations de Navier-Stokes :
- À gauche, on retrouve la variation de la vitesse d'une parcelle de fluide selon le temps et l'espace.
- À droite, on retrouve trois termes dans l'ordre habituel :
- celui de la variation de pression qui contient en son sein un terme de correction pour la force centripète induite par le mouvement de rotation
- celui de diffusion et de convection par la viscosité
- celui de la force de Coriolis avec la vitesse de rotation
Si le taux de rotation devient important, on peut négliger le deuxième terme de droite de l'équation car les forces de Coriolis et centripète deviennent dominantes. On peut alors multiplier par un rotationnel les deux côtés de l'équation et résoudre l'équation vectorielle résultante ainsi :
Les solutions à cette équation donnent la représentation des ondes inertielles qui doivent satisfaire aux conditions suivantes :
1) , Où représente donc une onde transverse (perpendiculaire au mouvement).
et
2) , Où est l'angle entre l'axe de rotation et la direction de l'onde.
Caractéristiques[modifier | modifier le code]
La première condition de la solution de ces équations définit que la force de restauration est perpendiculaire au mouvement. De plus, la résolution de ces équations donne des ondes dont la vitesse de phase, qui donne son mouvement, est perpendiculaire à celle de groupe qui donne la direction du transport d'énergie. Cela donne des ondulations qui conduisent d'une manière similaire à la variation des champs électriques et magnétiques dans une onde électromagnétique par rapport à sa propagation.
La seconde condition implique que les solutions à ces équations ont des valeurs entre 0 et 2 fois le taux de rotation du repère seulement dans un système ouvert. En réalité, dans un système réel, comme l'océan ou l'atmosphère, certaines restrictions diminuent le choix et donnent des valeurs discrètes.
Bibliographie[modifier | modifier le code]
- K. D. Aldridge et I. Lumb: Inertial waves identified in the Earth's fluid outer core dans Nature, vol.325, p. 421-423 , 1987
- H. P. Greenspan : The Theory of Rotating Fluids par Cambridge University Press, 1969
- L. D. Landau et E. M. Lifschitz : Fluid Mechanics, Seconde édition par Elsevier, New York (ISBN 0750627670)
- S. Galtier: "A Weak Inertial Wave Turbulence Theory", Phys. Rev. E, vol.68, p 015301, 2003.







![{\displaystyle {\frac {\partial }{\partial t}}[{\vec {\nabla }}\times {\vec {u}}]=2({\vec {\Omega }}\cdot {\vec {\nabla }}){\vec {u}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3df7f38c92425a85d8b2b40051986ecc994d83f)



