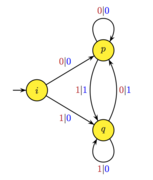
Machine de Mealy

En informatique théorique, notamment en théorie des automates, et en théorie de la calculabilité, une machine de Mealy ou automate de Mealy est un transducteur fini (i.e. un automate fini avec une sortie) pour lequel les sorties dépendent à la fois de l'état courant et des symboles d'entrée. Cela signifie que l'étiquette de chaque transition est un couple formé d'une lettre d'entrée et d'une lettre de sortie. En particulier, la longueur du mot de sortie est égale à la longueur du mot d'entrée.
Cette définition est plus générale que celle des machines de Moore pour lesquelles les valeurs de sortie ne dépendent que de l'état courant. Toutefois, il existe pour chaque machine de Mealy, une machine de Moore équivalente et réciproquement.
Cet automate tient son nom de George H. Mealy, qui a proposé ce modèle en 1955[1]. Ils font maintenant partie des concepts de base en théorie des automates et des langages rationnels et figurent dans de nombreux manuels[2],[3],[4], [5].
Les automates de Mealy ont des applications en théorie géométrique des groupes, où ils interviennent, depuis les travaux de Rostislav Grigorchuk, dans la définition de groupes d'automorphismes à croissance intermédiaire.
Définition formelle[modifier | modifier le code]
Une machine de Mealy est constituée des données suivantes :
- un ensemble fini d'états ;
- un état initial , élément de ;
- un ensemble fini , appelé alphabet d'entrée ;
- un ensemble fini , appelé alphabet de sortie ;
- une fonction de transition ;
- une fonction de sortie .
Il est commode de noter l'état par et le symbole de sortie par . La fonction de transition et la fonction de sortie sont étendues aux mots de par récurrence, pour et , par
En d'autres termes, la sortie produite par le mot lu à partir de l'état est le mot produit par le mot lu à partir de l'état , suivi de la lettre produite par le symbole lu à partir de l'état atteint après la lecture de .
La fonction réalisée par l’automate de Mealy est l'application définie par:
C'est donc la fonction qui, à un mot de lu à partir de l'état initial , associe le mot sur obtenu en concaténant les lettres de sortie des transitions parcourues.
Variante[modifier | modifier le code]
Parfois, une machine de Mealy est dotée d'un ensemble fini d'état terminaux. La fonction réalisée est alors restreinte aux mots du langage rationnel sur l'alphabet d'entrée reconnu par l'automate.
Exemples[modifier | modifier le code]
Décalage[modifier | modifier le code]
Dans l'exemple ci-dessus, le mot produit par la lecture d'un mot à partir de l'état initial consiste à préfixer par la lettre , puis à recopier à l'exception de sa dernière lettre. Par exemple :
Le résultat est donc le décalage de l’entrée d'un chiffre, avec perte du dernier symbole.
« Ou » exclusif (addition modulo 2)[modifier | modifier le code]
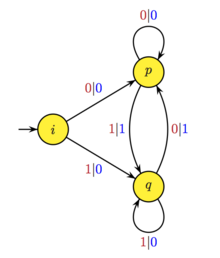
L'automate ci-contre réalise le « ou » exclusif ou addition modulo 2 des deux chiffres binaires consécutifs de l'entrée, avec recopie du premier symbole. Cette propriété est utilisée par exemple dans la détection de contour. Les entrées sont représentées en rouge, les sorties en bleu. Soit la fonction réalisée. On obtient par exemple
Applications[modifier | modifier le code]
Les machines de Mealy fournissent un modèle mathématique rudimentaire pour représenter le chiffrement des informations. Supposons que l'alphabet d'entrée et l'alphabet de sortie soient constituées de l'ensemble des chaînes de caractères latins. Il est possible de concevoir une machine de Mealy transformant une chaîne de caractères en clair (entrée) en une chaîne chiffrée (sortie). Cet exemple est toutefois théorique : par exemple, s'il est possible de décrire la machine de chiffrement Enigma en utilisant une machine de Mealy, le diagramme états-transitions reste trop complexe pour une interprétation efficace.
Transformation d'une machine de Mealy en machine de Moore[modifier | modifier le code]
Pour transformer une machine de Mealy en machine de Moore, on peut procéder en trois étapes comme suit :
- Étape 1 : Dupliquer les états et détourner les transitions entrantes.
Chaque état est dupliqué en autant d'exemplaires qu'il y a de symboles de sorties sur les transitions entrant dans cet état. Les transitions entrantes sont détournées de manière que lorsqu'elles entrent dans un état, elles aient toutes le même symbole de sortie ;
- Étape 2 : Écrire les sorties dans les états.
Pour chaque transition, on reporte le symbole de sortie dans l'état d'arrivée. Grâce à la duplication préalable des états, il y a un seul symbole de sortie associé à un état ;
- Étape 3 : Dupliquer les transitions sortantes.
Les transitions sortantes d'un état sont dupliquées sur chaque copie d'état réalisée à l'étape 1.
L'automate obtenu est un automate de Moore équivalent à l'automate de Mealy de départ. Son nombre d'états est au plus , où est l'ensemble d'états de l'automate de Mealy, et est l'alphabet de sortie.
-
Automate de départ.
-
Étape 1. Duplication des états.
-
Étape 2. Écriture des sorties dans les états.
-
Étape 3. Duplication des transitions sortantes.
Automates de Mealy et demi-groupes à croissance intermédiaire[modifier | modifier le code]

Les automates de Mealy sont des modèles utilisés en théorie des groupes pour décrire des groupes ou des demi-groupes de transformations. Ils se prêtent notamment à la construction de groupes et demi-groupes à croissance dite « intermédiaire », ni polynomiale ni exponentielle. Les premiers groupes ont été mis en évidence par Rostislav Grigorchuk (le groupe de Grigorchuk). Le plus petit automate qui donne un demi-groupe à croissance intermédiaire est décrit en détail par Bartholdi et al.[6] et est appelé l'« automate de Sushchanskii » par Bartholdi [7].

Les automates de Mealy inversibles à deux états et sur deux lettres, qui donnent des groupes de transformations, ont été tous décrits, par R. I. Grigorchuk, V. V. Nekrashevich et V. I. Sushchanskiĭ[8]. Les demi-groupes de transformation deux lettres définis par des automates de Mealy sur deux états sont aussi connus[6]. Parmi eux, il y a l'automate de Sushchanskiĭ qui a la particularité que son taux de croissance, intermédiaire, est connu ; il est
Les automates considérés sont des automates Mealy particuliers : ils ont même alphabet d'entrée et de sortie, en général , et n'ont pas d'états initiaux ni terminaux. Les états sont en bijection avec les générateurs du groupe ou demi-groupe, augmentés de l'automorphisme identité. Les transitions sont les quadruplets tels que dans le demi-groupe, où et sont des généraleurs du demi-groupe ou l'identité. On voit qu'il existe un chemin de à d'étiquette d'entrée et d'étiquette de sortie , soit et si et seulement si . Par exemple, il y a dans l’automate de Grigorchuk un chemin
représentant le calcul
- .
L'étude des automates de Mealy et des groupes et demi-groupes de transformations qu'ils définissent a été poursuivie par Thibault Godin, Inès Klimann, Matthieu Picantin[9].
Formellement, tout état réalise une fonction , notée aussi quand il n'y a pas de confusion possible, vérifiant et appelée transformation automatique associée à . Les fonctions réalisées peuvent être composées : si est associée à l’état , alors , en d'autres termes la sortie de la fonction associée à devient l’entrée de la fonction associée à . Les mots et ont même longueur. Plus généralement, on associe à tout mot , produit de générateurs du demi-groupe, une fonction définie par composition des fonctions des générateurs.
Le taux de croissance est le nombre d'éléments distincts du demi-groupe qui produit de générateurs sans être produit de moins de générateurs.
Les demi-groupes à deux états et à deux symboles se répartissent en deux demi-groupes finis, sept demi-groupes à croissances polynomiale, un à croissance intermédiaire (l'automate de Sushchanskii), et huit demi-groupes à croissance exponentielle, y compris le demi-groupe libre[7].
Plusieurs types d'automates de Mealy existent : un automate est inversible si les étiquettes de sortie des transitions d'un état sont toutes distinctes. Alors chaque état définit une permutation sur les étiquettes de sortes. L'automate de Grigorchuk est inversible, l'automate de Sushchanskii ne l’est pas puisque les deux transitions de l’état le même symbole de sortie. Le demi-groupe engendré par un automate inversible est un groupe. Le dual d'un automate est l'automate obtenu en échangeant les états et les lettres : formellement, chaque transition donne une transition du dual. Un automate est réversible quand les fonctions de transitions de l’automate sont des permutations de l’ensemble des états ou, de manière équivalente, quand son dual est inversible[10]. Un exemple d'automate inversible est l'automate dit du groupe de l’allumeur de réverbères, en anglais « lamplighter group »[11],[12]. Comme il s'agit d'automates inversibles sur deux lettres, les transitions sortant d'un état sont soit et , soit et . Une écriture remontant aux premiers travaux de Grigorchuk et toujours utilisée consiste à étiqueter un état par 1 ou par ε selon qu'il est de la première ou de la deuxième espèce, et de ne pas indique explicitement la sortie sur les transitions ; ainsi, une transition est remplacée par . Une autre famille est constituée des automates biréversibles[13].
- Automates du groupe de l'allumeur de réverbères
-
Automate de l'allumeur de réverbères.
-
Inverse de l'automate.
-
Dual de l'automate.
-
Variante de représentation.
Notes et références[modifier | modifier le code]
- George H. Mealy, « A Method for Synthesizing Sequential Circuits », Bell System Tech. J. 34 (1955) : 1 045–1 079.
- (en) W.M.L. Holcombe, Algebraic automata theory, vol. 1, Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics », (ISBN 0-521-60492-3, zbMATH 0489.68046)
- Jean-Eric Pin, chap. I/9 « Algorithmique et Programmation. Automates finis », dans Jacky Akoka et Isabelle Comyn-Wattiau (éditeurs), Encyclopédie de l’informatique et des systèmes d’information, Paris, Vuibert, (ISBN 978-2711748464, lire en ligne), p. 966-976
- Jean-Éric Pin, « Petit cours sur les fonctions séquentielles », Sainte-Marie de Ré, sur www.irif.fr, LIAFA, CNRS et Université Denis Diderot, mai 2013, (consulté le ).
- Jacques Sakarovitch, Éléments de théorie des automates, Vuibert, , 816 p. (ISBN 978-2-7117-4807-5). — Traduction anglaise (par Reuben Thomas) : Elements of Automata Theory, Cambridge University Press 2009, (ISBN 9780521844253).
- (en) Laurent Bartholdi, Ilya I. Reznykov et Vitalii I. Sushchansky, « The smallest Mealy automaton of intermediate growth », Journal of Algebra, vol. 295, no 2, , p. 387–414 (ISSN 0021-8693, DOI 10.1016/j.jalgebra.2004.08.040, arXiv math/0407312v1, lire en ligne).
- Laurent Bartholdi, « Decidability problems in automaton semigroups », preprint, (arXiv 1705.04598v1).
- R.I. Grigorchuk, V.V. Nekrashevich et V.I. Sushchanskiĭ, « Automata, dynamical systems, and groups », Proc. Steklov Inst. Math., vol. 231, , p. 128–203 (MR 1841755).
- Thibault Godin, Ines Klimann et Matthieu Picantin, « On torsion-free semigroups generated by invertible reversible Mealy automata », LATA 2015, Springer, , p. 328–339 (DOI 10.1007/978-3-319-15579-1_25, MR 3344813, arXiv abs/1410.4488).
- Thibault Godin, Machines de Mealy, (semi-)groupes d’automate, problèmes de décision et génération aléatoire, thèse de doctorat, Université Paris Diderot, (lire en ligne).
- (en) Rostislav I. Grigorchuk et Andrzej Żuk, « The lamplighter group as a group generated by a 2-state automaton, and its spectrum », Geometriae Dedicata, vol. 87, nos 1-3, , p. 209–244 (ISSN 0046-5755, DOI 10.1023/A:1012061801279).
- (en) Ali Akhavi, Ines Klimann, Sylvain Lombardy, Jean Mairesse et Matthieu Picantin, « On the finiteness problem for automaton (semi)groups », Int. J. Algebra Comput., vol. 22, no 6, , p. 1–26 (zbMATH 1280.20038, arXiv 1105.4725).
- (en) Thibault Godin et Ines Klimann, « On bireversible Mealy automata and the Burnside problem », Theoretical Computer Science, vol. 707, , p. 24–35 (DOI 10.1016/j.tcs.2017.10.005).