Transducteur fini

En informatique théorique, en linguistique, et en particulier en théorie des automates, un transducteur fini (appelé aussi transducteur à états finis par une traduction littérale de l'anglais finite state transducer) est un automate fini avec sorties. C'est une extension des automates finis. Ils opèrent en effet sur les mots sur un alphabet d'entrée et, au lieu de simplement accepter ou refuser le mot, ils le transforment, de manière parfois non déterministe, en un ou plusieurs mots sur un alphabet de sortie. Ceci permet des transformations de langages, et aussi des utilisations variées telles que notamment l'analyse syntaxique des langages de programmation, et l'analyse morphologique ou l'analyse phonologique en linguistique.

Une des propriétés remarquables des transducteurs finis est qu'ils transforment les langages rationnels en langages rationnels, et les langages algébriques en langages algébriques.

Définitions formelles[modifier | modifier le code]

Un transducteur fini est une machine mathématique qui transforme des mots. Une telle machine est conçue sur le modèle des automates finis, avec, pour chaque transition, une étiquette additionnelle sous forme d'un mot. Chaque transition est donc dotée de deux étiquettes. Ceci est fréquemment représenté par l'écriture

q{\xrightarrow {\ a|b\ }}r

Le symbole $a$ est l' étiquette d'entrée, le symbole $b$ est l' étiquette de sortie de la transition. De manière imagée, on dit que le transducteur « lit » le symbole $a$ et « écrit » le symbole $b$ en passant de l'état $q$ à l'état $r$ . En itérant cette action un transducteur lit un mot de gauche à droite sur son ruban d'entrée et écrit un mot sur son ruban de sortie.

La finitude du transducteur signifie la finitude du nombre d'états. Mais comme souvent en informatique théorique, les machines sont — en principe — non déterministes, c'est-à-dire qu'il existe plusieurs exécutions où un même mot est lu, mais les états pris par la machine et les mots écrits peuvent différer dans les différentes exécutions.

Les transducteurs finis ont de nombreuses propriétés théoriques, et des applications pratiques nombreuses, par exemple en compilation, en reconnaissance de la parole et en linguistique.

Transducteur fini[modifier | modifier le code]

Un transducteur fini est défini par un 6-uple

T=(\Sigma _{1},\Sigma _{2},Q,I,F,\delta )

, où :

$\Sigma _{1}$ est l'alphabet fini d'entrée ;

$\Sigma _{2}$ est l'alphabet fini de sortie ;

$Q$ est l'ensemble fini des états ;

$I\subseteq Q$ est l'ensemble des états initiaux ;

$F\subseteq Q$ est l'ensemble des états finaux ;

$\delta$ est la table de transition : c'est un sous-ensemble de $Q\times (\Sigma _{1}\cup \{\varepsilon \})\times (\Sigma _{2}\cup \{\varepsilon \})\times Q$ où $\varepsilon$ est le mot vide.

La propriété $(q,a,b,r)\in \delta$ signifie qu'il existe une transition de l'état $q$ vers l'état $r$ par laquelle on lit le symbole $a\in \Sigma _{1}\cup \{\varepsilon \}$ sur le ruban d'entrée et on écrit le symbole $b\in \Sigma _{2}\cup \{\varepsilon \}$ sur le ruban de sortie. Ceci est fréquemment représenté par la notation

q\,{\xrightarrow {a|b}}\,r

Le symbole $a$ est l'étiquette d'entrée, le symbole $b$ est l'étiquette de sortie de la transition^[1].

Si $|T(w)|\leq 1$ pour tout $w\in {\Sigma _{1}}^{*}$ , alors le transducteur T est dit fonctionnel.

Clôture transitive[modifier | modifier le code]

La clôture transitive $\delta ^{*}$ de $\delta$ est la plus petite relation (pour l'inclusion des relations) vérifiant :

$\delta ^{*}\subseteq Q\times \Sigma _{1}^{*}\times \Sigma _{2}^{*}\times Q$

$\delta \subseteq \delta ^{*}$

$\forall q\in Q,(q,\varepsilon ,\varepsilon ,q)\in \delta ^{*}$ (réflexivité)

Si $(q,x,y,r)\in \delta ^{*}$ et $(r,a,b,s)\in \delta$ , alors $(q,xa,yb,s)\in \delta ^{*}$ (transitivité)

En d'autres termes, $(q,x,y,r)\in \delta ^{*}$ signifie qu'il existe un chemin de l'état $q$ vers l'état $r$ dont l'étiquette d'entrée est le mot $x\in \Sigma _{1}^{*}$ et l'étiquette de sortie est le mot $y\in \Sigma _{2}^{*}$ . Un chemin est réussi si $q\in I$ et $r\in F$ .

Relation rationnelle[modifier | modifier le code]

Par analogie avec les automates finis qui reconnaissent un langage, un transducteur fini $T$ reconnaît une relation, notée $[T]$ du produit cartésien des deux monoïdes libres. On a $(x,y)\in [T]$ ou $x[T]y$ si et seulement s'il existe $p\in I$ et $r\in F$ tel que $(p,x,y,r)\in \delta ^{*}$ . En d'autres termes, $x$ est en relation avec $y$ si et seulement s'il existe un chemin réussi qui lit $x$ et écrit $y$ .

Variante de définition[modifier | modifier le code]

Dans une variante de la définition, au lieu de demander que les étiquettes des transitions soient des lettres ou le mot vide, on autorise comme étiquettes des mots sur l'alphabet d'entrée resp. l'alphabet de sortie.

Les différentes façons de considérer un transducteur fini[modifier | modifier le code]

Un transducteur fini peut être vu de plusieurs façons, ce qui permet des utilisations tout à fait différentes.

Transducteur vu comme un automate[modifier | modifier le code]

Dans le cas où aucune des étiquettes du transducteur n'est le mot vide, on peut voir un transducteur comme un cas particulier des automates finis. Il vérifie alors les propriétés classiques des automates.

Il suffit en effet de considérer un automate dont l'alphabet est le produit cartésien des deux alphabets : $\Sigma =\Sigma _{1}\times \Sigma _{2}$ .

Transducteur vu comme une relation rationnelle[modifier | modifier le code]

Le fait de considérer un transducteur comme une relation rationnelle permet d'établir une propriété primordiale dans l'étude et l'utilisation de ceux-ci : la clôture par composition.

Opérations sur les transducteurs[modifier | modifier le code]

Opérations héritées des automates[modifier | modifier le code]

Union : soient $A$ et $B$ deux transducteurs finis. On définit un transducteur fini, noté $A\cup B$ tel que $[A\cup B]=[A]\cup [B]$ .

Produit de concaténation : soient $A$ et $B$ deux transducteurs, alors il existe un transducteur noté $A\cdot B$ tel que $u[A\cdot B]v$ si et seulement s'il existe des décompositions $u=xx'$ et $v=yy'$ telles que $x[A]y$ et $x'[B]y'$ . En d'autres termes, $[A\cdot B]=\{(xx',yy')\mid (x,y)\in [A],(x',y')\in [B]\}$ .

Étoile de Kleene : soit $T$ , alors il existe un transducteur noté $T^{*}$ qui correspond à l'étoile pour l'opération de concaténation.

Attention, l'intersection de relations rationnelles n'est pas nécessairement rationnelle (l'intersection de deux relations $R$ et $R'$ est la relation $R''$ définie par $R''=R\cap R'$ )

Composition[modifier | modifier le code]

Considérons deux transducteurs finis $T_{1}$ et $T_{2}$ tels que l'alphabet de sortie de $T_{1}$ coïncide avec l'alphabet d'entrée de $T_{2}$ .

Le composé $T_{3}=T_{2}\circ T_{1}$ est défini par la relation $[T_{3}]$ :

$x[T_{3}]y\Leftrightarrow \exists z$ tel que $x[T_{1}]z$ et $z[T_{2}]y$ .

Il est important de noter que la composition de deux transducteurs finis est encore un transducteur fini. Ainsi la composition permet d'élaborer facilement des transducteurs ayant une fonction complexe à partir de transducteurs simples.

Projections[modifier | modifier le code]

Projection gauche : la projection gauche d'une relation $R$ est l'ensemble $K=\{x\mid \exists y:(x,y)\in R\}$ . Soit $T$ un transducteur fini. La projection gauche de la relation $[T]$ est un langage rationnel: il existe automate fini qui la reconnaît; il suffit en effet d’« oublier » les étiquettes de sortie sur les transitions de $T$ .

Projection droite : de même, la projection droite d'une relation rationnelle est un langage rationnel.

Autres propriétés des transducteurs finis[modifier | modifier le code]

Le problème consistant à déterminer si un transducteur fini est fonctionnel est décidable^[2].
Le problème consistant à déterminer s'il existe un mot $w$ tel que $T(x)=w$ pour un $x$ donné est décidable.
L'équivalence entre deux transducteurs finis n'est pas décidable dans le cas général^[3]. Elle est néanmoins décidable dans le cas des transducteurs finis déterministes^[4]^,^[5] et dans le cas où le transducteur réalise une fonction partielle.
Si, pour un transducteur fini $T$ fonctionnel, $T(\epsilon )=\emptyset$ ou $T(\epsilon )=\{\epsilon \}$ , alors on peut construire un transducteur fini fonctionnel déterministe équivalent^[6].

Application à l'analyse grammaticale[modifier | modifier le code]

Dans cette section, nous donnons deux exemples de transducteurs. Étant donné une phrase, le but est de générer une suite qui donne la nature grammaticale de chaque mot de la phrase. Par exemple, si la phrase est « Alex aime les frites » alors le but est de générer la séquence NOM VERBE ARTICLE NOM. Pour cela, on définit deux transducteurs.

Le premier transducteur, noté $L$ (pour Lexique), transforme une séquence de lettres suivies d'une espace en un mot, si le mot fait partie du lexique.

Un deuxième transducteur, noté $D$ (pour Dictionnaire), transforme un mot en sa nature grammaticale (ou éventuellement plusieurs si le mot possède plusieurs natures grammaticales).

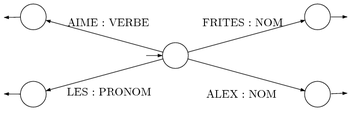
Ainsi, il suffit de considérer le transducteur composé $T=D^{*}\circ L^{*}$ . Comme la composition préserve la fonction des transducteurs, ce nouveau transducteur prendra en entrée une séquence de lettres, et écrira en sortie une séquence de natures grammaticales correspondant aux mots de la phrase.

Extension du modèle : transducteur fini pondéré[modifier | modifier le code]

De même que pour les automates finis, les transducteurs finis peuvent être améliorés en les pondérant. La méthode est d'ailleurs identique à celle utilisée pour les automates fini pondérés.

Une telle optimisation peut se voir utilisée par exemple dans des correcteurs d'orthographe. Pour cela, il suffit de définir une distance entre les mots comme d(u, v) = nombre de modifications nécessaires pour transformer u en v. Il suffit alors de définir un transducteur qui réalise des transformations élémentaires (changement de lettre, ajout d'une lettre, suppression d'une lettre) en pondérant correctement ces transformations.

Ainsi, à chaque fois qu'un mot n'existe pas dans le dictionnaire, une comparaison de ce mot aux autres par l'intermédiaire du transducteur pondéré déterminera quel mot correct est le plus proche.

Restrictions sur le modèle[modifier | modifier le code]

Selon les conditions que l'on impose au transducteur, il réalise des relations ou des fonctions plus restreintes. Quand le transducteur est déterministe en entrée, les transductions sont dites séquentielles ; ce sont des fonctions appelées elles-mêmes fonctions séquentielles. Quand de plus les étiquettes d'entrée et de sortie des transitions sont des lettres, les fonctions réalisées préservent les longueurs ; les automates sont les automates de Mealy^[7]^,^[8].

Articles connexes[modifier | modifier le code]

Références[modifier | modifier le code]

↑ On note comme d'usage par $\Sigma ^{*}$ le monoïde libre des mots sur l'alphabet $\Sigma$ .
↑ M.P. Schützenberger. Sur les relations rationnelles, Automata Theory and Formal Languages, 2nd GI Conference, Lecture Notes in Computer Science, volume 33, pp. 209–213, 1975.
↑ (en) Griffiths, T. The unsolvability of the equivalence problem for Λ-free nondeterministic generalized machines, Journal of the Association for Computing Machinery 15, 1968, pp. 409-413
↑ (en) Eitan M. Gurari, The equivalence problem for deterministic two-way sequential transducers is decidable. SIAM J. Comput. , 11(3):448–452, 1982.
↑ (en) Tero Harju, Juhani Karhumäki, The equivalence problem of multitape finite automata, Theoretical Computer Science vol. 78, 1991, pp.347-355
↑ Samuel Eilenberg. Automata, Languages and Machines, volume A. Academic Press, 1974.
↑ Jean-Eric Pin, chap. I/9 « Algorithmique et Programmation. Automates finis », dans Jacky Akoka et Isabelle Comyn-Wattiau (éditeurs), Encyclopédie de l’informatique et des systèmes d’information, Paris, Vuibert, 2006 (ISBN 978-2711748464, HAL hal-00143940/document), p. 966-976
↑ Jean-Éric Pin, « Petit cours sur les fonctions séquentielles », Sainte-Marie de Ré, LIAFA, CNRS et Université Denis Diderot, mai 2013 (consulté le 3 août 2017)

Bibliographie complémentaire[modifier | modifier le code]

Stefan Gerdjikov, Stoyan Mihov et Klaus U. Schulz, « Space-efficient bimachine construction based on the equalizer accumulation principle », Theoretical Computer Science, vol. 790,‎ 2019, p. 80–95 (ISSN 0304-3975, DOI 10.1016/j.tcs.2019.04.027).

Portail de l'informatique théorique

[1] On note comme d'usage par $\Sigma ^{*}$ le monoïde libre des mots sur l'alphabet $\Sigma$ .

[2] M.P. Schützenberger. Sur les relations rationnelles, Automata Theory and Formal Languages, 2nd GI Conference, Lecture Notes in Computer Science, volume 33, pp. 209–213, 1975.

[3] (en) Griffiths, T. The unsolvability of the equivalence problem for Λ-free nondeterministic generalized machines, Journal of the Association for Computing Machinery 15, 1968, pp. 409-413

[4] (en) Eitan M. Gurari, The equivalence problem for deterministic two-way sequential transducers is decidable. SIAM J. Comput. , 11(3):448–452, 1982.

[5] (en) Tero Harju, Juhani Karhumäki, The equivalence problem of multitape finite automata, Theoretical Computer Science vol. 78, 1991, pp.347-355

[6] Samuel Eilenberg. Automata, Languages and Machines, volume A. Academic Press, 1974.

[7] Jean-Eric Pin, chap. I/9 « Algorithmique et Programmation. Automates finis », dans Jacky Akoka et Isabelle Comyn-Wattiau (éditeurs), Encyclopédie de l’informatique et des systèmes d’information, Paris, Vuibert, 2006 (ISBN 978-2711748464, HAL hal-00143940/document), p. 966-976

[8] Jean-Éric Pin, « Petit cours sur les fonctions séquentielles », Sainte-Marie de Ré, LIAFA, CNRS et Université Denis Diderot, mai 2013 (consulté le 3 août 2017)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

v · m Automates finis et langages réguliers
Articles généraux	Théorie des automates Automate fini Machine abstraite
Automates finis	Automate fini déterministe Automate fini inambigu Automate fini non déterministe Construction par sous-ensembles Automate sur les mots infinis
Automates finis particuliers	Automate alternant Automate bidirectionnel Automate pondéré Automate probabiliste Automate quantique Automate temporisé Automate de Büchi Automate de Muller Modèle de Markov caché Système de transition d'états Structure de Kripke Machine à états abstraits Machine de Mealy Machine de Moore Transducteur fini Automate séquentiel
Langages réguliers	Langage rationnel Langage sans étoile Langage local Langage congruentiel Langage stochastique Lemme de l'étoile Lemme d'Arden ω-langage rationnel
Des automates aux langages	Expression régulière Algorithme de Conway Algorithme de McNaughton et Yamada Méthode de Brzozowski et McCluskey
Des langages aux automates	Dérivée de Brzozowski Algorithme de Thompson Construction de Glushkov Complexité en états
Minimisation	Théorème de Myhill-Nerode Équivalence de Nerode Minimisation d'un automate fini déterministe Algorithme de Moore Algorithme de Brzozowski Algorithme de Hopcroft
Équivalences	Théorème de Kleene Étoile de Kleene Monoïde syntaxique Théorème des variétés d'Eilenberg