Automate de Büchi

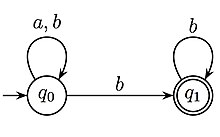
En informatique théorique, un automate de Büchi est un ω-automate ou automate fini opérant sur des mots infinis, avec une condition d'acceptation particulière : une trace (ou calcul ou chemin infini) est réussie si et seulement si elle passe un nombre infini de fois par au moins un état acceptant. Un mot infini est accepté s'il est l'étiquette d'un calcul réussi. Ce type d'automate est utilisé en vérification de modèles.

Ce type d'automate a été défini par le mathématicien Julius Richard Büchi^[1].

Définition[modifier | modifier le code]

Un automate de Büchi sur un alphabet $A$ est un ω-automate ${\mathcal {A}}=(Q,{\mathcal {F}},I,T)$ , où :

$Q$ est un ensemble fini d'états ;
${\mathcal {F}}\subset Q\times A\times Q$ est l'ensemble des transitions ;
$I\subseteq Q$ est l'ensemble des états initiaux ;
$T\subseteq Q$ est un ensemble d'états finals ou terminaux ou acceptants.

Souvent on suppose que l'ensemble des états initiaux est composé d'un seul élément^[2]. Une transition $f=(p,a,q)$ est composée d'un état de départ $p$ , d'une étiquette $a$ et d'un état d'arrivée $q$ . Un calcul $c$ (on dit aussi un chemin ou une trace) est une suite infinie de transitions consécutives :

c=(p_{0},a_{1},p_{1})(p_{1},a_{2},p_{2})\cdots

Son état de départ est $p_{0}$ , son étiquette est le mot infini $a_{1}a_{2}\cdots a_{n}\cdots$ . Le calcul est réussi et le mot est accepté ou reconnu s'il passe infiniment souvent par un état terminal.

Un automate est déterministe s'il vérifie les deux conditions suivantes :

il possède un seul état initial ;
pour tout état $q$ , et pour toute lettre $a$ , il existe au plus une transition partant de $q$ et portant l'étiquette $a$ .

Exemples[modifier | modifier le code]

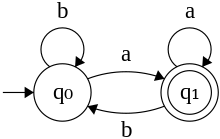
L'automate de Büchi déterministe donné par ${\mathcal {A}}=(\{q_{0},q_{1}\},{\mathcal {F}},q_{0},\{q_{1}\})$ , avec deux états : $q_{0}$ et $q_{1}$ . L'état $q_{0}$ est initial. L'ensemble des états acceptants est $T=\{q_{1}\}$ . La fonction de transition ${\mathcal {F}}$ est montrée dans le dessin à gauche.

Le mot infini $bbbb\cdots$ n'est pas accepté car la seule trace correspondante est $q_{0}q_{0}q_{0}\cdots$ et le seul état qui apparaît une infinité de fois est $q_{0}$ qui ne figure pas dans $T$ . Par contre, le mot $aaaa\cdots$ est accepté car il possède la trace $q_{0}q_{1}q_{1}\cdots$ , et $q_{1}$ y apparaît une infinité de fois et est dans $T$ . Il reconnaît les mots infinis contenant un nombre infini de $a$ . En rencontrant la lettre $b$ , l'automate retourne dans l'état $q_{0}$ , alors qu'une lecture de la lettre $a$ met l'automate dans l'état $q_{1}$ . Plus généralement, l'automate accepte exactement les mots infinis sur deux lettres $a$ et $b$ qui ne contiennent qu'un nombre fini de lettres $a$ , c'est-à-dire l'ensemble $b^{*}a(a^{*}b^{+}a)^{\omega }$ .

{\displaystyle b} — Automate de Büchi reconnaissant les mots infinis où chaque occurrence de $b$ est précédé d'un nombre pair non nul de $a$ .

Un autre exemple est l'automate de Büchi à droite ; il reconnaît les mots infinis où chaque occurrence de $b$ est précédé d'un nombre pair non nul de $a$ . L'automate possède trois états : $q_{0}$ , $q_{1}$ et $q_{2}$ . Il est aussi déterministe. L'automate démarre dans l'état $q_{0}$ et lit un nombre pair non nul de $a$ . Si l'automate a lu un nombre impair de $a$ , il est dans l'état $q_{1}$ , sinon dans l'état $q_{2}$ . La transition $b$ de l'état $q_{2}$ à l'état $q_{0}$ permet de lire la lettre $b$ après un nombre pair non nul de $a$ . Une lecture de $b$ depuis $q_{0}$ ou $q_{1}$ échoue.

Déterminisme versus non-déterminisme[modifier | modifier le code]

Les automates de Büchi déterministes sont strictement moins puissants que les automates de Büchi non déterministes^[3]^,^[4]. Par exemple, alors qu'il existe un automate de Büchi non déterministe à deux états qui reconnaît les mots infinis sur deux lettres $a$ et $b$ qui ne contiennent qu'un nombre fini de lettres $a$ , c'est-à-dire l'ensemble $\{a,b\}^{*}b^{\omega }$ , cet ensemble n'est pas reconnu par un automate de Büchi déterministe.

Supposons le contraire, c'est-à-dire qu'il existe un automate de Büchi déterministe qui reconnaît ce langage, et soit $F$ son ensemble d'états d'acceptation. L'automate accepte le mot infini $b^{\omega }$ , dont le calcul passe une première fois dans un état de $F$ après la lecture d'un certain nombre positif, disons $n$ , de lettres $b$ . L'automate accepte aussi le mot infini $b^{n}ab^{\omega }$ , donc le calcul passe une deuxième fois par un état de $F$ après disons $m$ lettres $b$ . L'automate accepte donc le mot $b^{n}ab^{m}ab^{\omega }$ . De proche en proche, on construit un mot $b^{n_{1}}ab^{n_{2}}ab^{n_{3}}ab\cdots$ contenant une infinité de lettres $a$ et qui est accepté par l’automate, contradiction.

Langages reconnus[modifier | modifier le code]

Les ensembles de mots infinis reconnus par les automates de Büchi sont les ensembles rationnels de mots infinis ou ω-langages rationnels, à savoir les ensembles de la forme

\bigcup _{1}^{m}U_{i}V_{i}^{\omega }

où les $U_{i}$ et $V_{i}$ sont des langages rationnels pour tout $i$ , les $V_{i}$ ne contenant pas le mot vide. Ces langages sont aussi appelés les ω-fermeture de Kleene des langages rationnels^[5].

La formule pour l'expression du langage reconnu par un automate de Büchi s'obtient comme suit : étant donné une automate de Büchi, notons $W(p,q)$ l’ensemble des mots finis reconnus avec $p$ comme état initial et $q$ comme état final, donc les mots qui sont étiquettes d’un chemin de $p$ à $q$ . Ces langages (de mots finis) sont rationnels. Un mot infini $x$ est accepté s’il existe un calcul qui passe une infinité de fois par un état final, donc aussi s’il existe un état final disons $q$ , par lequel il passe une infinité de fois. Ceci est équivalent à dire que

x\in W(q_{0},q)W(q,q)^{\omega }

pour un état initial $q_{0}$ . En prenant la réunion sur tous les états initiaux et terminaux, on obtient la description indiquée^[5]. Pour démontrer que réciproquement tous les ω-langages rationnels sont reconnus par des automates de Büchi, on utilise les opérations de fermeture de la section suivante^[6].

La description effective des ω-langages rationnels reconnus montre que le problème du mot est décidable pour les automates de Büchi, puisqu’il suffit de tester si l’un au moins des langages rationnels $W(q_{0},q)W(q,q)$ n’est pas vide.

Propriétés de clôture[modifier | modifier le code]

Les langages reconnus par des automates de Büchi fermés pour un certain nombre d'opérations qui se reflètent dans des constructions sur les automates.

Union : Soient ${\mathcal {A}}=(Q_{A},{\mathcal {F}}_{A},I_{A},T_{A})$ et ${\mathcal {B}}=(Q_{B},{\mathcal {F}}_{B},I_{B},T_{B})$ reconnaissant respectivement les langages $L_{A}$ et $L_{B}$ . Un automate reconnaissant la réunion $L_{A}\cup L_{B}$ s'obtient en faisant la réunion des deux automates. On suppose les ensembles d'états de ${\mathcal {A}}$ et ${\mathcal {B}}$ disjoints ; alors l’automate ${\mathcal {C}}=(Q_{A}\cup Q_{B},{\mathcal {F}}_{A}\cup {\mathcal {F}}_{B},I_{A}\cup I_{B},T_{A}\cup T_{B})$ reconnaît la réunion.

ω-fermeture : Pour tout langage rationnel $L$ ne contenant pas le mot vide, le ω-langage $L^{\omega }$ est reconnu par un automate de Büchi. Soit ${\mathcal {A}}=(Q,{\mathcal {F}},i,T)$ un automate fini reconnaissant $L$ . On peut supposer qu'il n'a qu'un seul état initial noté $i$ , et qu'il n'y a pas de transition entrant dans $i$ . On ajoute à l'automate ${\mathcal {A}}$ les transitions $(q,a,i)$ pour chaque transition $(q,a,t)$ de ${\mathcal {F}}$ avec $t\in T$ . L'automate de Büchi ainsi construit, avec un seul état initial qui est aussi terminal, reconnaît $L^{\omega }$ .

Concaténation : Pour tout langage rationnel $L$ et tout ω-langage $M$ reconnu par un automate de Büchi, le produit $LM$ est un ω-langage reconnu par un automate de Büchi. Soient en effet ${\mathcal {A}}=(Q,{\mathcal {F}},i,T)$ un automate fini reconnaissant $L$ , avec $I\cap T=\emptyset$ , et ${\mathcal {B}}=(Q',{\mathcal {F'}},I',T')$ un automate de Büchi reconnaissant $M$ . On peut supposer les ensembles d'états des deux automates disjoints. On peut aussi supposer que $L$ ne contient pas le mot vide, sinon on remplace le produit $LM$ par $(L\setminus \varepsilon )M\cup M$ . On construit un automate de Büchi ${\mathcal {C}}$ qui a pour états l'union des ensembles d'états, pour transitions l'union des ensembles de transitions, augmentées des transitions $(q,a,i')$ pour $i'\in I'$ pour chaque transition $(q,a,t)$ de ${\mathcal {F}}$ qui mène vers un état terminal $t$ de ${\mathcal {A}}$ . Enfin, ses états initiaux sont ceux de ${\mathcal {A}}$ et ses états terminaux ceux de ${\mathcal {B}}$ . Formellement, ${\mathcal {C}}=(Q'\cup Q,{\mathcal {F}}\cup {\mathcal {F'}}\cup {\mathcal {G}},I,T')$ avec ${\mathcal {G}}=\{(q,a,i')\mid i'\in I',(q,a,t)\in {\mathcal {F}},t\in T\}$ .

Ces trois propriétés démontrent que tout ω-langage rationnel est reconnaissable par un automate de Büchi.

Intersection : Soient ${\mathcal {A}}=(Q_{A},{\mathcal {F}}_{A},I_{A},T_{A})$ et ${\mathcal {B}}=(Q_{B},{\mathcal {F}}_{B},I_{B},T_{B})$ reconnaissant respectivement les langages $L_{A}$ et $L_{B}$ . Un automate reconnaissant l'intersection $L_{A}\cap L_{B}$ est construit de la manière suivante : ${\mathcal {C}}=\{Q_{A}\times Q_{B}\times \{0,1,2\},Q_{A}\times Q_{b}\times \{0\},{\mathcal {F}},T\}$ , où les transitions de ${\mathcal {F}}$ copient celles de ${\mathcal {F_{A}}}$ et ${\mathcal {F_{B}}}$ pour les deux premières composantes, et changent la troisième composante de 0 en 1 quand un état de $T_{A}$ apparaît dans la première composante, de 1 en 2 quand ensuite un état de $T_{B}$ apparaît dans la deuxième composantes, et retourne en 0 immédiatement après. Dans un calcul, un 2 apparaît infiniment souvent en troisième composante si et seulement un état de $T_{A}$ et un état de $T_{B}$ apparaissent infiniment souvent en première et en deuxième composante. Donc, en choisissant pour états terminaux de $Q_{A}\times Q_{b}\times \{2\}$ on obtient un automate de Büchi au comportement désiré^[7].

Les langages reconnus par des automates de Büchi sont fermés par complémentation. Büchi en a donné une démonstration en 1962^[1]. Plus tard, d'autres constructions de l'automate reconnaissant les langages complémentaires ont été développées^[8]^,^[9]^,^[10]^,^[11].

Lien avec les autres modes de reconnaissance[modifier | modifier le code]

Les automates de Büchi sont équivalents aux automates de Muller, aux automates de Rabin, automates de Streett ou automates de parité. Cependant, ils différent par leur concision. Par exemple, les automates de Büchi sont exponentiellement plus concis que les automates de Rabin dans le sens suivant : il existe une famille de langages (L_n)_n=2.. sur l'alphabet {0, 1, #}, reconnaissable par des automates de Büchi non-déterministes de taille O(n) mais tout automate de Rabin non-déterministe équivalent doit être de taille au moins n!^[12].

Les automates de Büchi non déterministes représentent exactement les propriétés de la logique monadique de second ordre à un successeur (S1S), dites aussi propriétés ω-régulières^[13]. La logique S1S est strictement plus expressive que la logique temporelle linéaire.

Il existe une condition duale à l'acceptation des automates de Büchi : il s'agit des automates co-Büchi. La condition d'acceptation est alors : une trace (ou calcul ou chemin infini) est réussie si et seulement si tout état apparaissant un nombre fini de fois est un état acceptant^[14].

Algorithmique[modifier | modifier le code]

Logique du temps linéaire et model checking[modifier | modifier le code]

On utilise les automates de Büchi en vérification de modèles (model checking) où des questions algorithmiques se posent. Par exemple, savoir si le langage d'un automate de Büchi non-déterministe est vide se décide en temps linéaire^[15]. On peut traduire une formule de la logique temporelle linéaire (LTL) en un automate de Büchi, mais dont la taille est exponentielle en la taille de la formule LTL^[16]. Cette transformation peut servir à :

décider le problème de satisfiabilité de LTL. Ce problème est PSPACE-complet, mais voici un algorithme en temps exponentiel : construire un automate de Büchi équivalent à la formule LTL puis tester si son langage est vide ;
Faire de la vérification de modèles (model checking). Pour cela, on construit l'automate de Büchi équivalent à la formule LTL et on fait le produit avec le système à vérifier. Le produit est un automate de Büchi et il faut tester si son langage est vide.

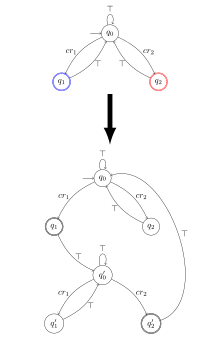
La transformation d'une formule LTL en un automate de Büchi est généralement présenté avec un intermédiaire, appelé automate de Büchi généralisé, où la condition d'acceptation est plus générale. Un automate de Büchi généralisé est comme un automate de Büchi, sauf que l'ensemble d'états terminaux $T\subseteq Q$ est remplacé par une famille finie $\{T_{1},\dots ,T_{k}\}$ où $T_{i}\subseteq Q$ . La condition d'acceptation devient : une trace (ou calcul ou chemin infini) est réussie si et seulement si pour tout i, elle passe un nombre infini de fois par au moins un état acceptant de $T_{i}$ . Dans la figure ci-contre, l'automate du haut est un automate de Büchi correspondant à des mots sur l'alphabet { $\top$ , cr1, cr2}. L'exemple provient de la propriété $\varphi$ "infiniment souvent dans la section critique 1, et infiniment souvent dans la section critique 2". La lettre $\top$ correspond à une section non critique, cr1 correspond à la section critique 1 et cr2 à la section critique 2. La famille $T\subseteq Q$ est {{q₁}, {q₂}}. Une exécution acceptante, doit passer infiniment souvent par q1 et infiniment souvent par q2. Cela correspond bien à la propriété $\varphi$ .

On transforme d'abord la formule LTL en un automate de Büchi généralisé (l'idée est que les états de l'automate sont les sous-ensemble maximaux consistants de sous-formules de la formule LTL). Par exemple, la propriété $\varphi$ s'écrit en LTL : $GFcr_{1}\land GFcr_{2}$ (toujours dans le futur cr1 et toujours dans le futur cr2). L'automate généralisé est donné dans la figure ci-contre, automate du haut. On transforme alors cet automate en un automate de Büchi usuel : il est obtenu en faisant une copie de l'automate généralisé pour chaque sous-ensemble $T_{i}$ . Dans l'exemple, l'automate est recopié deux fois : la première copie correspond à {q₁} et la deuxième à {q₂}. Une fois q₁ rencontré, on passe dans la seconde copie. Une fois q₂' rencontré, on repasse dans la première copie. L'automate obtenu est un automate de Büchi classique est la condition d'acceptation est de passer une infinité de fois par q₁ ou q₂'. Par construction, cette condition est équivalente à passer une infinité de fois dans q₁ et une infinité de fois dans q₂ dans l'automate généralisé.

Il existe des algorithmes efficaces en pratique pour construire un automate de Büchi équivalent à partir d'une formule LTL^[17].

Il existe des algorithmes pour l'« apprentissage » d'un automate de Büchi^[18].

S1S et WS1S[modifier | modifier le code]

Büchi^[1] a montré qu'il y a équivalence, pour tout langage de mots infinis L, entre :

L est définissable par une propriété S1S (logique monadique de second ordre à un successeur) ;
L est définissable par une propriété WS1S (logique monadique de second ordre à un successeur, dite "weak", c'est-à-dire que la quantification du second ordre porte sur les ensembles finis) ;
L est reconnaissable par un automate de Büchi.

Les équivalences sont effectives : on transforme une formule S1S en un automate de Büchi. Ainsi, la logique S1S (et WS1S) est décidable. La logique S1S est de complexité non élémentaire^[19].

Notes[modifier | modifier le code]

↑ ^{a b et c} Julius R. Büchi, « On a decision method in restricted second order arithmetic », Proc. International Congress on Logic, Method, and Philosophy of Science (1960), Stanford University Press,‎ 1962, p. 1-12.
↑ Par exemple : Farwer 2002.
↑ Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, 31 mai 2008, 975 p. (ISBN 978-0-262-02649-9 et 9780262026499, lire en ligne), p. 191
↑ Erich Grädel, Wolfgang Thomas et Thomas Wilke, Automata logics, and infinite games : a guide to current research, Springer-Verlag New York, Inc., 1^er janvier 2002, 385 p. (ISBN 978-3-540-00388-5, lire en ligne), p. 11, sous-section 1.4.1
↑ ^{a et b} Farwer 2002, p. 6.
↑ Thomas 1990, p. 138-139.
↑ Thomas 1990, p. 138.
↑ Robert McNaughton, « Testing and generating infinite sequences by a finite automaton », Information and Control, vol. 9,‎ 1966, p. 521-530 (DOI 10.1016/s0019-9958(66)80013-x).
↑ A. P. Sistla, M. Y. Vardi et P. Wolper, « The complementation problem for Büchi automata with applications to temporal logic », Theoretical Computer Science, vol. 49,‎ 1987, p. 217–237 (DOI 10.1016/0304-3975(87)90008-9).
↑ S. Safra, « On the complexity of ω-automata », Proc. 29th IEEE Symposium on Foundations of Computer Science, White Plains, New York,‎ octobre 1988, p. 319–327.
↑ O. Kupferman et M. Y. Vardi, « Weak alternating automata are not that weak », ACM Transactions on Computational Logic, vol. 2, n^o 2,‎ juillet 2001, p. 408–429.
↑ Erich Grädel, Wolfgang Thomas et Thomas Wilke, Automata logics, and infinite games : a guide to current research, Springer-Verlag New York, Inc., 1^er janvier 2002, 385 p. (ISBN 978-3-540-00388-5, lire en ligne), p. 18, Theorem 1.30.
↑ Thomas 1990, p. 144-146.
↑ (en) Guillaume Sadegh, Laboratoire de Recherche et Développement de l’Epita, Complementing Büchi Automata, t. 0903, révision 2073 (Technical Report), Le Kremlin-Bicêtre, mai 2009 (lire en ligne)
↑ Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, 31 mai 2008, 975 p. (ISBN 978-0-262-02649-9 et 9780262026499, lire en ligne), p. 185, Th. 4.42
↑ Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, 31 mai 2008, 975 p. (ISBN 978-0-262-02649-9 et 9780262026499, lire en ligne)
↑ (en) Paul Gastin et Denis Oddoux, « Fast LTL to Büchi Automata Translation », Computer Aided Verification, Springer, Berlin, Heidelberg, lecture Notes in Computer Science,‎ 18 juillet 2001, p. 53–65 (ISBN 3540445854, DOI 10.1007/3-540-44585-4_6, lire en ligne, consulté le 7 février 2018)
↑ Yong Li, Yu-Fang Chen, Lijun Zhang et Depeng Liu, « A novel learning algorithm for Büchi automata based on family of DFAs and classification trees », Information and Computation, vol. 281,‎ décembre 2021, article n^o 104678 (DOI 10.1016/j.ic.2020.104678).
↑ « Luke Ong - Automata, Logic and Games: Theory and Application 1. Büchi Automata and S1S »

Références[modifier | modifier le code]

Wolfgang Thomas, « Automata on infinite objects », dans : Jan Van Leeuwen (éditeur), Handbook of Theoretical Computer Science: Formal Models and Semantics, t. B, MIT Press, 1990, 1287 p. (ISBN 0-262-72015-9), p. 133-192
Berndt Farwer, « ω-Automata », dans : Erich Grädel, Wolfgang Thomas et Thomas Wilke (éditeurs), Automata, logics, and infinite games : A guide to current research, Springer-Verlag, coll. « Lecture Notes in Computer Science » (n^o 2500),‎ 2002, viii+385 (ISBN 978-3-540-00388-5), p. 3-22.
Samuel Eilenberg, Automata, Languages and Machines, Vol. A, Academic Press, coll. « Pure and Applied Mathematics » (n^o 58), 1974, xvi+451 (ISBN 978-0-12-234001-7), « Chap. XIV. Infinite Behavior of Finite Automata », p. 379-393.

Portail de l'informatique théorique

[:0-1] {a b et c} Julius R. Büchi, « On a decision method in restricted second order arithmetic », Proc. International Congress on Logic, Method, and Philosophy of Science (1960), Stanford University Press,‎ 1962, p. 1-12.

[2] Par exemple : Farwer 2002.

[3] Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, 31 mai 2008, 975 p. (ISBN 978-0-262-02649-9 et 9780262026499, lire en ligne), p. 191

[4] Erich Grädel, Wolfgang Thomas et Thomas Wilke, Automata logics, and infinite games : a guide to current research, Springer-Verlag New York, Inc., 1^er janvier 2002, 385 p. (ISBN 978-3-540-00388-5, lire en ligne), p. 11, sous-section 1.4.1

[Farwer-5] {a et b} Farwer 2002, p. 6.

[6] Thomas 1990, p. 138-139.

[7] Thomas 1990, p. 138.

[8] Robert McNaughton, « Testing and generating infinite sequences by a finite automaton », Information and Control, vol. 9,‎ 1966, p. 521-530 (DOI 10.1016/s0019-9958(66)80013-x).

[9] A. P. Sistla, M. Y. Vardi et P. Wolper, « The complementation problem for Büchi automata with applications to temporal logic », Theoretical Computer Science, vol. 49,‎ 1987, p. 217–237 (DOI 10.1016/0304-3975(87)90008-9).

[10] S. Safra, « On the complexity of ω-automata », Proc. 29th IEEE Symposium on Foundations of Computer Science, White Plains, New York,‎ octobre 1988, p. 319–327.

[11] O. Kupferman et M. Y. Vardi, « Weak alternating automata are not that weak », ACM Transactions on Computational Logic, vol. 2, n^o 2,‎ juillet 2001, p. 408–429.

[12] Erich Grädel, Wolfgang Thomas et Thomas Wilke, Automata logics, and infinite games : a guide to current research, Springer-Verlag New York, Inc., 1^er janvier 2002, 385 p. (ISBN 978-3-540-00388-5, lire en ligne), p. 18, Theorem 1.30.

[13] Thomas 1990, p. 144-146.

[14] (en) Guillaume Sadegh, Laboratoire de Recherche et Développement de l’Epita, Complementing Büchi Automata, t. 0903, révision 2073 (Technical Report), Le Kremlin-Bicêtre, mai 2009 (lire en ligne)

[15] Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, 31 mai 2008, 975 p. (ISBN 978-0-262-02649-9 et 9780262026499, lire en ligne), p. 185, Th. 4.42

[16] Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, 31 mai 2008, 975 p. (ISBN 978-0-262-02649-9 et 9780262026499, lire en ligne)

[17] (en) Paul Gastin et Denis Oddoux, « Fast LTL to Büchi Automata Translation », Computer Aided Verification, Springer, Berlin, Heidelberg, lecture Notes in Computer Science,‎ 18 juillet 2001, p. 53–65 (ISBN 3540445854, DOI 10.1007/3-540-44585-4_6, lire en ligne, consulté le 7 février 2018)

[18] Yong Li, Yu-Fang Chen, Lijun Zhang et Depeng Liu, « A novel learning algorithm for Büchi automata based on family of DFAs and classification trees », Information and Computation, vol. 281,‎ décembre 2021, article n^o 104678 (DOI 10.1016/j.ic.2020.104678).

[19] « Luke Ong - Automata, Logic and Games: Theory and Application 1. Büchi Automata and S1S »

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

v · m Automates finis et langages réguliers
Articles généraux	Théorie des automates Automate fini Machine abstraite
Automates finis	Automate fini déterministe Automate fini inambigu Automate fini non déterministe Construction par sous-ensembles Automate sur les mots infinis
Automates finis particuliers	Automate alternant Automate bidirectionnel Automate pondéré Automate probabiliste Automate quantique Automate temporisé Automate de Büchi Automate de Muller Modèle de Markov caché Système de transition d'états Structure de Kripke Machine à états abstraits Machine de Mealy Machine de Moore Transducteur fini Automate séquentiel
Langages réguliers	Langage rationnel Langage sans étoile Langage local Langage congruentiel Langage stochastique Lemme de l'étoile Lemme d'Arden ω-langage rationnel
Des automates aux langages	Expression régulière Algorithme de Conway Algorithme de McNaughton et Yamada Méthode de Brzozowski et McCluskey
Des langages aux automates	Dérivée de Brzozowski Algorithme de Thompson Construction de Glushkov Complexité en états
Minimisation	Théorème de Myhill-Nerode Équivalence de Nerode Minimisation d'un automate fini déterministe Algorithme de Moore Algorithme de Brzozowski Algorithme de Hopcroft
Équivalences	Théorème de Kleene Étoile de Kleene Monoïde syntaxique Théorème des variétés d'Eilenberg