« Quadrilatère circonscriptible » : différence entre les versions
Redirection |
Créé en traduisant la page « Tangential quadrilateral » Balises : Redirection supprimée Traduction de contenu Traduction de contenu 2 |
||
| Ligne 1 : | Ligne 1 : | ||
#REDIRECTION[[Quadrilatère inscriptible]] |
|||
[[Fichier:Tangential_quadrilateral_2.svg|vignette|300x300px| Un quadrilatère circonscriptible avec son cercle inscrit]] |
|||
En [[géométrie euclidienne]], un '''quadrilatère circonscriptible''' (ou '''quadrilatère tangentiel''') est un [[quadrilatère]] [[Polygone convexe|convexe]] pour lequel il existe un [[cercle inscrit]], c'est-à-dire un cercle situé à l'intérieur du quadrilatère et [[Tangente à un cercle|tangent]] à chacun de ses quatre côtés<ref>{{Article|langue=fr|auteur1=G.-H. Nievengloski|titre=Sur le quadrilatère circonscriptible, et sur l’égalité des polygones|périodique=Nouvelles annales de mathématiques|série=1|volume=11|date=1852|lire en ligne=http://www.numdam.org/item/NAM_1852_1_11__462_1.pdf|format=pdf|pages=462-463}}</ref><ref>{{Lien web |auteur=Patrice Debart |titre=Les quadrilatères au collège |url=https://debart.pagesperso-orange.fr/college/quadrilatere.mobile.html#tangentiel |site=debart.pagesperso-orange.fr |consulté le=2023-01-03}}</ref><ref name=":0">{{Article|langue=en|auteur1=Martin Josefsson|titre=More Characterizations of Tangential Quadrilaterals|périodique=Forum Geometricorum|volume=11|date=2011|lire en ligne=http://forumgeom.fau.edu/FG2011volume11/FG201108.pdf|format=pdf|pages=65-82}}</ref><ref>{{Lien web |langue=en |prénom=Eric W. |nom=Weisstein |titre=Tangential Quadrilateral |url=https://mathworld.wolfram.com/ |site=mathworld.wolfram.com |consulté le=2023-01-03}}</ref>. On dit alors que le quadrilatère ''circonscrit'' son cercle inscrit. Un quadrilatère circonscriptible est un cas particulier de [[polygone circonscriptible]]. |
|||
Si tout [[triangle]] est circonscriptible, ce n'est pas toujours vrai pour un quadrilatère. Par exemple, un [[rectangle]] n'est circonscriptible que si c'est un [[carré]] ; un rectangle ayant des côtés consécutifs de longueurs différentes n'est pas circonscriptible. Des [[Condition nécessaire et suffisante|conditions nécessaires et suffisantes]] pour qu'un quadrilatère soit circonscriptible sont détaillées ci-dessous. |
|||
== Exemples == |
|||
Les [[Cerf-volant (géométrie)|cerf-volants]] (y compris les [[Losange|losanges]] et les carrés) sont des quadrilatères circonscriptibles. Les cerf-volants sont d'ailleurs les quadrilatères qui sont à la fois [[Quadrilatère orthodiagonal|orthodiagonaux]] et circonscriptibles<ref name=":1">{{Article|langue=en|auteur1=Martin Josefsson|titre=Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral|périodique=Forum Geometricorum|volume=10|date=2010|lire en ligne=http://forumgeom.fau.edu/FG2010volume10/FG201013.pdf|format=pdf|pages=119-130}}</ref>. |
|||
Les [[Trapèze|trapèzes]] peuvent être également [[Trapèze circonscriptible|circonscriptibles]]. |
|||
Un quadrilatère peut être à la fois circonscriptible et [[Quadrilatère inscriptible|inscriptible]], c'est à dire que ses quatre sommets appartiennent à un même cercle, le [[Cercle circonscrit|cercle circonscrit.]] Un tel quadrilatère est dit [[Quadrilatère bicentrique|bicentrique]] et a donc à la fois un cercle inscrit et un cercle circonscrit. Par exemple, les cerfs-volants droits (ayant deux angles droits opposés) et les trapèzes circonscriptibles [[Trapèze isocèle|isocèles]] sont bicentriques. |
|||
== Caractérisations par les longueurs == |
|||
Dans un quadrilatère circonscriptible, les quatre [[Bissectrice|bissectrices]] des angles sont concourantes au centre du cercle inscrit. Réciproquement, un quadrilatère convexe dans lequel les quatre bissectrices sont concourantes est circonscriptible et leur point d'intersection est le centre du cercle inscrit<ref name=":2">{{Ouvrage|prénom1=Bogdan|nom1=Enescu|titre=Mathematical olympiad treasures|passage=64-68|éditeur=Birkhäuser|date=2011|isbn=978-0-8176-8253-8|isbn2=0-8176-8253-8|isbn3=978-0-8176-8252-1|oclc=757539145|lire en ligne=https://www.worldcat.org/oclc/757539145|consulté le=2023-01-03}}</ref>. |
|||
D'après le [[théorème de Pitot]], les sommes des longueurs des côtés deux à deux opposés sont égales entre elles, et égales au demi-périmètre ''s'' du quadrilatère. En notant ''a'', ''b'', ''c'' et ''d'' les longueurs successives des côtés, on a : |
|||
: <math>a + c = b + d = \frac{a + b + c + d}{2} = s.</math> |
|||
Réciproquement, tout quadrilatère convexe vérifiant ''a'' + ''c'' = ''b'' + ''d'' est nécessairement circonscriptible<ref name=":0" /><ref name=":2" />. |
|||
Si les côtés opposés d'un quadrilatère convexe ''ABCD'' (qui n'est pas un [[trapèze]]) se coupent en ''E'' et ''F'', alors il est tangentiel si et seulement si au moins l'une des deux équations suivantes est vraie<ref name=":2" /> : |
|||
: <math>\displaystyle BE+BF=DE+DF</math> |
|||
ou |
|||
: <math>\displaystyle AE-EC=AF-FC.</math> |
|||
Cette dernière équation est proche de l'une des équations du [[Quadrilatère ex-tangentiel|théorème d'Urquhart]], à ceci près que dans ce dernier l'équation relie les sommes des longueurs et non leur différence. |
|||
Un quadrilatère convexe ''ABCD'' est circonscriptible si et seulement si les cercles inscrits dans les deux triangles ''ABC'' et ''ADC'' sont [[Tangente (géométrie)|tangents]] l'un à l'autre<ref name=":0" />. |
|||
Une caractérisation par les angles entre la diagonale ''BD'' et les quatre côtés d'un quadrilatère ABCD, affirme qu'un quadrilatère est circonscriptible si et seulement si les angles vérifient<ref name=":3">{{Article|langue=en|auteur1=Nicusor Minculete|titre=Characterizations of a Tangential Quadrilateral,|périodique=Forum Geometricorum|volume=9|date=2009|lire en ligne=http://forumgeom.fau.edu/FG2009volume9/FG200910.pdf|format=pdf|pages=113-118}}</ref> : |
|||
: <math>\tan{\frac{ \widehat{ABD}}{2}}\cdot\tan{\frac{\widehat{ BDC}}{2}}=\tan{\frac{\widehat{ADB}}{2}}\cdot\tan{\frac{\widehat{DBC}}{2}}.</math> |
|||
[[Fichier:Tangential-quad-external-circles.svg|gauche|vignette| Un quadrilatère circonscriptible (en bleu) avec son cercle inscrit (ligne pointillée) et les quatre cercles extérieurs tangents (en rouge), chacun tangent à un côté donné et aux prolongements des deux côtés adjacents.]] |
|||
De plus, un quadrilatère convexe de côtés de longueurs ''a'', ''b'', ''c'', ''d'' est circonscriptible si et seulement si |
|||
: <math>R_aR_c=R_bR_d</math> |
|||
où ''R''<sub>''a''</sub>, ''R''<sub>''b''</sub>, ''R''<sub>''c''</sub>, ''R''<sub>''d''</sub> sont les rayons des cercles extérieurs tangents au côté de longueurs respectives ''a'', ''b'', ''c'', ''d'' et aux prolongements des deux côtés adjacents<ref>{{Article|langue=en|auteur1=Martin Josefsson|titre=Similar Metric Characterizations of Tangential and Extangential Quadrilaterals|périodique=Forum Geometricorum|volume=12|date=2012|lire en ligne=http://forumgeom.fau.edu/FG2012volume12/FG201207.pdf|format=pdf|pages=63-77}}</ref>. |
|||
== Points de contacts et cordes de tangence == |
|||
[[Fichier:Tangency_chords_2.svg|vignette|300x300px| Un quadrilatère inscriptible (en bleu) et son quadrilatère de contact (en vert) les cordes de tangence (en rouge) et les huit longueurs tangentes (en noir).]] |
|||
Le cercle inscrit est tangent aux quatre côtés en quatre points de contact. Le quadrilatère formé par ces quatre points est appelé ''quadrilatère de contact''. |
|||
Dans un quadrilatère circonscriptible, les longueurs des segments reliant un [[Sommet (géométrie)|sommet]] aux points de contact entre les côtés et le cercle inscrit sont appelées ''longueurs tangentes'' (notées ''e'', ''f'', ''g'', ''h'' dans la figure de droite). Les deux longueurs tangentes issues d'un même sommet sont égales. |
|||
Les deux ''cordes de tangence'' (notées ''k'' et ''l'' sur la figure) sont les segments qui relient les points de contact des côtés opposés. Ce sont aussi les [[Diagonale|diagonales]] du quadrilatère de contact . |
|||
== Aire == |
|||
=== Formules non trigonométriques === |
|||
L'[[Aire (géométrie)|aire]] ''S'' d'un quadrilatère circonscriptible est donnée par |
|||
: <math>\displaystyle S = r \cdot s,</math> |
|||
où ''s'' est le demi-périmètre et ''r'' est le rayon du cercle inscrit . Une autre formule est<ref name=":4">{{Ouvrage|prénom1=A.|nom1=Robson|prénom2=C.|nom2=Durell|titre=Advanced trigonometry|passage=28-30|éditeur=Dover Publications|date=2003|isbn=0-486-43229-7|isbn2=978-0-486-43229-8|oclc=52509659|lire en ligne=https://www.worldcat.org/oclc/52509659|consulté le=2023-01-03}}</ref> |
|||
: <math>\displaystyle S |
|||
= \tfrac{1}{2}\sqrt{p^2q^2-(ac-bd)^2}</math> |
|||
où l'aire est exprimée en fonction des longueurs des diagonales ''p'', ''q'' et des côtés ''a'', ''b'', ''c'', ''d'' du quadrilatère. |
|||
L'aire d'un peut également être calculée à partir des quatre longueurs tangentes ''e'', ''f'', ''g'', ''h'' ; le quadrilatère a alors pour aire<ref name=":1" /> : |
|||
: <math>\displaystyle S=\sqrt{(e+f+g+h)(efg+fgh+ghe+hef)}.</math> |
|||
Il existe également une formule d'aire faisant intervenir à la fois les longueurs des côtés ''a, b, c, d'' et les longueurs tangentes ''e, f, g, h'' <ref name=":1" /> : |
|||
: <math>S=\sqrt{abcd-(eg-fh)^2}.</math> |
|||
Or, on a ''eg'' = ''fh'' si et seulement si le quadrilatère circonscriptible est également inscriptible. On en conclut que, à longueurs de côtés données, un quadrilatère circonscriptible d'aire maximale est bicentrique<ref name=":5">{{Article|langue=fr|auteur1=Mowaffaq Hajja|titre=A condition for a circumscriptible quadrilateral to be cyclic|périodique=Forum Geometricorum|volume=8|date=2008|lire en ligne=http://forumgeom.fau.edu/FG2008volume8/FG200814.pdf|format=pdf|pages=103-106}}</ref>, et son aire est égale à <math>\sqrt{abcd}</math>. |
|||
=== Formules trigonométriques === |
|||
Une formule [[Trigonométrie|trigonométrique]] donne l'aire en fonction des longueurs des côtés ''a'', ''b'', ''c'', ''d'' et d'une paire d'angles opposés<ref name=":4" /><ref name=":6">{{Lien web |langue=en |auteur=Darij Grinberg |titre=Circumscribed quadrilaterals revisited |url=http://www.cip.ifi.lmu.de/~grinberg/CircumRev.pdf |format=pdf}}</ref> : |
|||
: <math>\displaystyle S = \sqrt{abcd}\; \sin \frac{\hat A+ \hat C}{2} = \sqrt{abcd}\; \sin \frac{\hat B+ \hat D}{2},</math> |
|||
où <math>\hat A</math> est l'angle des côtés au point ''A, <math>\hat B</math>'' est l'angle en ''B'', etc. |
|||
On retrouve le résultat précédent concernant le quadrilatère circonscriptible d'aire maximale qui est également inscriptible puisque le [[Sinus (mathématiques)|sinus]] vaut 1 si les angles opposés sont [[Angle|supplémentaires]] . |
|||
Il existe une autre formule pour l'aire d'un quadrilatère circonscriptible ''ABCD'' faisant intervenir deux angles opposés et les distances entre les sommets et le centre ''I'' du cercle inscrit<ref name=":6" /> |
|||
: <math>S=\left(IA\cdot IC+IB\cdot ID\right)\sin\frac{\hat A+\hat C}{2}</math> |
|||
L'aire peut alors s'écrire en fonction de deux côtés adjacents et deux angles opposés<ref name=":4" />: |
|||
: <math>S=ab\sin{\frac{\hat B}{2}}\csc{\frac{\hat D}{2}}\sin \frac{\hat B+\hat D}{2}.</math> |
|||
Ou encore, en fonction des longueurs des côtés et de l'angle ''θ'' entre les diagonales |
|||
: <math>S=\tfrac{1}{2}|(ac-bd)\tan{\theta}|,</math> |
|||
Cette formule n'est valable que si les diagonales ne forment pas un angle droit (sans quoi la tangente n'est pas définie) |
|||
=== Inégalités === |
|||
Comme vu plus haut, l'aire d'un quadrilatère circonscriptible de côtés ''a'', ''b'', ''c'', ''d'' vérifie |
|||
: <math>S\le\sqrt{abcd}</math> |
|||
l'égalité étant valable si et seulement si c'est un quadrilatère bicentrique. |
|||
Le demi-périmètre ''s'' du quadrilatère vérifie quant à lui |
|||
: <math>s\ge 4r</math> |
|||
où ''r'' est le rayon du cercle inscrit. Il y a égalité si et seulement si le quadrilatère est un carré. Puisqu'on a ''S'' = ''rs'' on a l'inégalité |
|||
: <math>S\ge 4r^2</math> |
|||
où l'égalité est vraie si et seulement si le quadrilatère est un carré. |
|||
=== Propriétés de partitions === |
|||
[[Fichier:Tangentenviereck.png|vignette|200x200px| Quadrilatère circonscriptible et son cercle inscrit de rayon ''r'']] |
|||
Les quatre segments entre le centre du cercle inscrit et les points de tangence divisent le quadrilatère en quatre cerfs-volants droits. |
|||
Si une droite coupe un quadrilatère circonscriptible en deux [[Polygone|polygones]] d' aires égales et de périmètres égaux, alors cette droite passe par le centre du cercle inscrit<ref name=":2" />. |
|||
== Rayon du cercle inscrit == |
|||
Le rayon ''r'' du cercle inscrit dans un quadrilatère circonscriptible de côtés ''a'', ''b'', ''c'', ''d'' est donné par<ref name=":4" /> : |
|||
: <math>r=\frac{S}{s}=\frac{S}{a+c}=\frac{S}{b+d}</math> |
|||
où ''S'' est l'aire du quadrilatère et ''s'' son demi-périmètre. Le rayon ''r'' est également maximal (à longueur de côtés donnés) si et seulement si le quadrilatère est bicentrique. |
|||
Le rayon du cercle inscrit peut également s'écrire en fonction des longueurs tangentes ''e'', ''f'', ''g'', ''h'' définies plus haut<ref>{{Article|langue=en|auteur1=John P. Hoyt|titre=Quickies Q694|périodique=Mathematics Magazine|volume=57|numéro=4|date=1984|pages=239}}</ref> |
|||
: <math>\displaystyle r=\sqrt{\frac{efg+fgh+ghe+hef}{e+f+g+h}}.</math> |
|||
On dispose également d'une expression du rayon en fonction des distances entre le centre du cercle ''I'' et les sommets du quadrilatère circonscriptible ''ABCD'' . En posant ''u = AI'', ''v = BI'', ''x = CI'' et ''y = DI'', on a alors |
|||
: <math>r=2\sqrt{\frac{(\sigma-uvx)(\sigma-vxy)(\sigma-xyu)(\sigma-yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}</math> |
|||
où <math>\sigma=\tfrac{1}{2}(uvx+vxy+xyu+yuv)</math><ref>{{Article|auteur1=Martin Josefsson|titre=On the inradius of a tangential quadrilateral|périodique=Forum Geometricorum|volume=10|date=2010|lire en ligne=http://forumgeom.fau.edu/FG2010volume10/FG201005.pdf|pages=27-34}}</ref>. |
|||
Si les cercles inscrits dans les triangles ''ABC'', ''BCD'', ''CDA'', ''DAB'' ont des rayons <math>r_1, r_2, r_3, r_4</math> respectivement, alors le rayon du cercle inscrit au quadrilatère circonscriptible ''ABCD'' est donné par |
|||
: <math>r=\frac{G+\sqrt{G^2-4r_1r_2r_3r_4(r_1r_3+r_2r_4)}}{2(r_1r_3+r_2r_4)}</math> |
|||
où <math>G=r_1r_2r_3+r_2r_3r_4+r_3r_4r_1+r_4r_1r_2</math> . <ref>[[Alexander Bogomolny|Bogomolny, Alexander]] (2016), An Inradii Relation in Inscriptible Quadrilateral, ''Cut-the-knot'', .</ref> |
|||
== Formules d'angles == |
|||
Les angles au sommets A,B,C,D d'un quadrilatère circonscriptible peuvent également s'écrire en fonction des longueurs tangentes ''e'',''f'',''g'',''h''<ref name=":1" /> |
|||
: <math> \sin{\frac{\hat A}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(e + f)(e + g)(e + h)}},</math> |
|||
: <math> \sin{\frac{\hat B}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(f + e)(f + g)(f + h)}},</math> |
|||
: <math> \sin{\frac{\hat C}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(g + e)(g + f)(g + h)}},</math> |
|||
: <math> \sin{\frac{\hat D}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(h + e)(h + f)(h + g)}}.</math> |
|||
L'angle ''φ'' entre les cordes de tangence ''k'' et ''l'' est donné par |
|||
: <math> \sin{\varphi}=\sqrt{\frac{(e + f + g + h)(efg + fgh + ghe + hef)}{(e + f)(f + g)(g + h)(h + e)}}.</math> |
|||
== Diagonales == |
|||
Les longueurs des diagonales ''p'' = ''AC'' et ''q'' = ''BD'' ont également une expression en fonction des longueurs tangentes ''e'',''f'',''g'' et ''h'' associées aux sommets A,B,C et D du quadrilatère circonscriptible<ref name=":5" /> |
|||
: <math>\displaystyle p=\sqrt{\frac{e+g}{f+h}\Big((e+g)(f+h)+4fh\Big)},</math> |
|||
: <math>\displaystyle q=\sqrt{\frac{f+h}{e+g}\Big((e+g)(f+h)+4eg\Big)}.</math> |
|||
== Cordes de tangence == |
|||
Si ''e'', ''f'', ''g'' et ''h'' sont les longueurs tangentes d'un quadrilatère circonscriptible, alors les longueurs des cordes de tangence sont<ref name=":1" /> |
|||
: <math>\displaystyle k=\frac{2(efg+fgh+ghe+hef)}{\sqrt{(e+f)(g+h)(e+g)(f+h)}},</math> |
|||
: <math>\displaystyle l=\frac{2(efg+fgh+ghe+hef)}{\sqrt{(e+h)(f+g)(e+g)(f+h)}}</math> |
|||
où la corde de tangence de longueur ''k'' relie les côtés de longueurs ''a'' = ''e'' + ''f'' et ''c'' = ''g'' + ''h'', et celle de longueur ''l'' relie les côtés de longueurs ''b'' = ''f'' + ''g'' et ''d'' = ''h'' + ''e''. |
|||
Le rapport des carrés des longueurs des cordes de tangence est égal au rapport des côtés opposés correspondants<ref name=":1" />. |
|||
: <math>\frac{k^2}{l^2} = \frac{bd}{ac}.</math> |
|||
Les deux cordes de tangence |
|||
* sont [[Perpendicularité|perpendiculaires]] si et seulement si le quadrilatère circonscriptible a aussi un [[Cercle circonscrit|cercle]] circonscrit (c'est à dire s'il est bicentrique)<ref name=":1" />. |
|||
* ont des longueurs égales si et seulement si le quadrilatère est un cerf-volant<ref name=":7">{{Article|langue=en|auteur1=Martin Josefsson|titre=When is a Tangential Quadrilateral a Kite?|périodique=Forum Geometricorum|volume=11|date=2011|lire en ligne=http://forumgeom.fau.edu/FG2011volume11/FG201117.pdf|format=pdf|pages=165-174}}</ref>. |
|||
La corde de tangence entre les côtés ''AB'' et ''CD'' dans un quadrilatère circonscriptible ''ABCD'' est plus longue que celle entre les côtés ''BC'' et ''DA'' si et seulement si la [[Quadrilatère|bimédiane]] entre les côtés ''AB'' et ''CD'' est plus courte que celle entre les côtés ''BC'' et ''DA''<ref>{{Article|langue=en|auteur1=Martin Josefsson|titre=The Area of a Bicentric Quadrilateral|périodique=Forum Geometricorum|volume=11|date=2011|lire en ligne=http://forumgeom.fau.edu/FG2011volume11/FG201116.pdf|format=pdf|pages=155-165}}</ref>. |
|||
Si le quadrilatère circonscriptible ''ABCD'' a pour points de tangence ''W'' sur ''AB'' et ''Y'' sur ''CD'', et si la corde de tangence ''WY'' coupe la diagonale ''BD'' en ''M'', alors le rapport des longueurs des tangentes <math>\tfrac{BW}{DY}</math> est égal au rapport <math>\tfrac{BM}{DM}</math> des segments de diagonale ''BD''<ref>{{Lien web |auteur=Antonio Gutierrez |titre=Circumscribed Quadrilateral, Diagonal, Chord, Proportion. |url=https://gogeometry.com/problem/p152_circumscribed_quadrilateral_diagonal_chord.htm |site=gogeometry.com |consulté le=2023-01-03}}</ref>. |
|||
== Alignement de points == |
|||
Soient ''M<sub>1</sub>'' et ''M<sub>2</sub>'' respectivement les [[Milieu d'un segment|milieux]] des diagonales ''AC'' et ''BD'' d'un quadrilatère circonscriptible ''ABCD'', ''I'', et si les paires de côtés opposés se rencontrent en ''J'' et ''K'' avec ''M <sub>3</sub>'' étant le milieu de ''JK'', alors les points ''M <sub>3</sub>'', ''M <sub>1</sub>'', ''I'' et ''M <sub>2</sub>'' sont [[Alignement (géométrie)|colinéaires]]<ref name=":2" />. La droite qui les contient est la [[droite de Newton]] du quadrilatère. |
|||
Soient ''J'' et ''K'' les points d'intersection des prolongements des côtés opposés du quadrilatère circonscriptible ; et ''L'' et ''M'' les prolongements des côtés opposés de son quadrilatère de contact. Alors les quatre points ''J'', ''L'', ''K'' et ''M'' sont alignés<ref name=":8">{{Article|langue=en|auteur1=Martin Josefsson|titre=Characterizations of Bicentric Quadrilaterals|périodique=Forum Geometricorum|volume=10|date=2010|lire en ligne=http://forumgeom.fau.edu/FG2010volume10/FG201019.pdf|format=pdf|pages=165-173}}</ref>. |
|||
Soien''t T<sub>1</sub>'', ''T<sub>2</sub>'', ''T<sub>3</sub>'', ''T<sub>4</sub>'' les points de tangence respectifs entre le cercle inscrit et les côtés ''AB'', ''BC'', ''CD'' et ''DA'' ; et soient ''N<sub>1</sub>'', ''N<sub>2</sub>'', ''N<sub>3</sub>'', ''N<sub>4</sub>'' leurs [[Conjugué isotomique|conjugués isotomiques]] respectifs par rapport aux côtés correspondants (c'est à dire que ''N<sub>1</sub>'' est le point du segment ''AB'' tel que ''AT<sub>1</sub>'' =''N<sub>1</sub>B'' et ainsi de suite). On définit alors le ''point de Nagel'' du quadrilatère comme l'intersection des segments ''N<sub>1</sub> N<sub>3</sub>'' et ''N<sub>2</sub> N<sub>4</sub>''.Ces deux lignes coupent le [[périmètre]] du quadrilatère en deux parties égales. Le point de Nagel ''N'', le [[Quadrilatère|centre de gravité]] ''G'' et le centre du cercle inscrit ''I'' sont alignés dans cet ordre, et on a de plus ''NG'' = 2 ''GI''. Cette droite s'appelle la ''droite de Nagel'' du quadrilatère<ref>{{Article|auteur1=Alexei Myakishev|titre=On Two Remarkable Lines Related to a Quadrilateral|périodique=Forum Geometricorum|volume=6|date=2006|lire en ligne=http://forumgeom.fau.edu/FG2006volume6/FG200634.pdf|format=pdf|pages=289-295}}</ref>. |
|||
[[Fichier:Tangential orthocenter lines.svg|vignette|Alignement des orthocentres (en rose) des triangles constitué par les sommets du quadrilatère ''ABCD'' et le centre du cercle inscrit ''I'', et le point ''P'' d'intersection des diagonales (en vert).]] |
|||
Soit quadrilatère ''ABCD'' circonscriptible dont le cercle inscrit a pour centre centre ''I'' et dont les diagonales se coupent en ''P'', soient ''H1'', ''H2'', ''H<sub>3</sub>'', ''H<sub>4</sub>'' les [[Hauteur d'un triangle|orthocentres]] des triangles ''AIB'', ''BIC'', ''CID'', ''DIA'' . Alors les points ''P'', ''H<sub>1</sub>'', ''H<sub>2</sub>'', ''H<sub>3</sub>'', ''H<sub>4</sub>'' sont alignés<ref name=":6" />. |
|||
== Lignes concourantes et perpendiculaires == |
|||
Les deux diagonales et les deux cordes de tangence sont [[Droites concourantes|concourantes]]<ref name=":6" />. On peut le démontrer à l'aide du [[théorème de Brianchon]], à savoir qu'un hexagone dont tous les côtés sont tangents à une même [[conique]] a trois diagonales reliant les côtés opposés concourantes. À partir du quadrilatère, on forme un hexagone ayant deux [[Angle plat|angles plats]] en créant deux nouveaux sommets en deux points de tangence opposés ; les six côtés de cet hexagone sont tangents au cercle inscrit, de sorte que ses diagonales sont concourantes. Deux de ces diagonales sont les diagonales du quadrilatère, et la troisième diagonale de l'hexagone passe par les deux points de tangence opposés, ce qui prouve que la corde de tangence et les deux diagonales sont concourantes. On procède de même avec les deux autres point de tangence, ce qui prouve le théorème pour les quatre droites. |
|||
Si les prolongements des côtés opposés d'un quadrilatère circonscriptible se coupent en ''J'' et ''K'', et les diagonales se coupent en ''P'', alors ''JK'' est perpendiculaire au prolongement de ''IP'' où ''I'' est le centre du cercle inscrit<ref name=":8" />. |
|||
== Centre du cercle inscrit == |
|||
Le centre du cercle inscrit au quadrilatère circonscriptible se trouve sur sa [[droite de Newton]] (passant par les milieux des diagonales)<ref>{{Article|langue=en|auteur1=Nikolaos Dergiades|auteur2=Dimitris M. Christodoulou,|titre=The two incenters of an arbitrary convex quadrilateral|périodique=Forum Geometricorum|volume=17|date=2017|lire en ligne=http://forumgeom.fau.edu/FG2017volume17/FG201727.pdf|format=pdf|pages=245-254}}</ref>. |
|||
Le rapport de deux côtés opposés dans un quadrilatère circonscriptible peut être exprimé en termes de distances entre le centre ''I'' et les sommets<ref name=":6" /> |
|||
: <math>\frac{AB}{CD}=\frac{IA\cdot IB}{IC\cdot ID},\quad\quad \frac{BC}{DA}=\frac{IB\cdot IC}{ID\cdot IA}.</math> |
|||
Le produit de deux côtés adjacents dans un quadrilatère circonscriptible ''ABCD'' de centre ''I'' vérifie<ref>{{Ouvrage|prénom1=Zuming|nom1=Feng|titre=103 trigonometry problems : from the training of the USA IMO team|passage=176-177|éditeur=Birkhäuser|date=2005|isbn=0-8176-4334-6|isbn2=978-0-8176-4334-8|isbn3=978-0-8176-4432-1|oclc=288195598|lire en ligne=https://www.worldcat.org/oclc/288195598|consulté le=2023-01-03}}</ref> |
|||
: <math>AB\cdot BC=IB^2+\frac{IA\cdot IB\cdot IC}{ID}.</math> |
|||
Si ''I'' est le centre du cercle inscrit à un quadrilatère ''ABCD'', alors on a<ref name=":6" /> : |
|||
: <math>IA\cdot IC+IB\cdot ID=\sqrt{AB\cdot BC\cdot CD\cdot DA}.</math> |
|||
De plus, le centre du cercle inscrit ''I'' dans un quadrilatère ''ABCD'' est confondu avec le [[Quadrilatère|barycentre]] du quadrilatère si et seulement si |
|||
: <math>IA\cdot IC=IB\cdot ID.</math> |
|||
Si ''I'' est le centre du cercle inscrit à un quadrilatère ''ABCD'' et ''M<sub>p</sub>'' et ''M<sub>q</sub>'' sont respectivement les [[Milieu d'un segment|milieux]] des diagonales ''AC'' et ''BD'', alors : |
|||
: <math>\frac{IM_p}{IM_q}=\frac{IA\cdot IC}{IB\cdot ID}=\frac{e+g}{f+h}</math> |
|||
où ''e'', ''f'', ''g'' et ''h'' sont les longueurs tangentes respectives associées à ''A'', ''B'', ''C'' et ''D''. Par corollaire, le centre ''I'' se confond avec le barycentre si et seulement si ''I'' est le milieu du segment reliant les deux milieux des diagonales. |
|||
Si un [[mécanisme à quatre barres]] a forme d'un quadrilatère circonscriptible, il restera circonscriptible quel que soit la déformation du mécanisme, tant que le quadrilatère reste convexe<ref>{{Article|prénom1=Helen|nom1=Barton|titre=Discussions: On a Circle Attached to a Collapsible Four-Bar|périodique=The American Mathematical Monthly|volume=33|numéro=9|date=1926|issn=0002-9890|doi=10.2307/2299611|lire en ligne=https://www.jstor.org/stable/2299611|consulté le=2023-01-03|pages=462–465}}</ref>. Par exemple, si un carré est déformé en losange, il restera toujours circonscriptible, mais à un cercle inscrit plus petit. Si un côté est maintenu fixe alors que les autres sommets sont déplacés, le centre du cercle cercle inscrit décrit un cercle de rayon <math>\sqrt{abcd}/s</math> où ''a,b,c,d'' sont les côtés et ''s'' est le demi-périmètre. |
|||
== Caractérisations par les quatre triangles diagonaux == |
|||
[[Fichier:Chao_tangentual_quad_radii.svg|vignette|240x240px| Caractérisation par les rayons de cercles inscrits aux quatre triangles diagonaux]] |
|||
Soit P l'intersection des diagonales dans un quadrilatère convexe ''ABCD''. Les quatre triangles ''APB'', ''BPC'', ''CPD'', ''DPA'' formés par côtés du quadrilatères et les diagonales, et forment une partition du quadrilatère en quatre. |
|||
''Si r''<sub>1</sub>, ''r'' <sub>2</sub>, ''r''<sub>3</sub> et ''r''<sub>4</sub> les rayons des cercles inscrits à ces quatre triangles, le quadrilatère est circonscriptible si et seulement si<ref>{{Article|prénom1=Wu Wei|nom1=Chao|prénom2=Plamen|nom2=Simeonov|titre=When Quadrilaterals Have Inscribed Circles: 10698|périodique=The American Mathematical Monthly|volume=107|numéro=7|date=2000|issn=0002-9890|doi=10.2307/2589133|lire en ligne=https://www.jstor.org/stable/2589133|consulté le=2023-01-03|pages=657–658}}</ref> |
|||
: <math>\frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}.</math> |
|||
De même, soient ''h''<sub>1</sub>, ''h''<sub>2</sub>, ''h''<sub>3</sub> et ''h''<sub>4</sub> les [[Hauteur d'un triangle|hauteurs]] respectives des quatre triangles cités précédemment issues de leur sommet commun (l'intersection des diagonales); le quadrilatère est tangentiel si et seulement si<ref name=":3" /> |
|||
: <math>\frac{1}{h_1}+\frac{1}{h_3}=\frac{1}{h_2}+\frac{1}{h_4}.</math> |
|||
On a également avec les les rayons des [[Cercles inscrit et exinscrits d'un triangle|cercles exinscrits]] aux quatre triangles diagonaux ''r''<sub>''a''</sub>, ''r''<sub>''b''</sub>, ''r''<sub>''c''</sub> et ''r''<sub>''d''</sub> dans les quatre mêmes triangles (les cercles étant tangents à un côté du quadrilatère et au prolongement des diagonales.). Le quadrilatère est circonscriptible si et seulement si<ref name=":0" /> : |
|||
: <math>\frac{1}{r_a}+\frac{1}{r_c}=\frac{1}{r_b}+\frac{1}{r_d}.</math> |
|||
Enfin si ''R''<sub>1</sub>, ''R''<sub>2</sub>, ''R''<sub>3</sub> et ''R''<sub>4</sub> sont respectivement les rayons dans les [[Cercle circonscrit|cercles circonscrits]] aux triangles ''APB'', ''BPC'', ''CPD'' et ''DPA'', alors le quadrilatère ''ABCD'' est circonscriptible si et seulement si<ref>{{Article|langue=en|auteur1=Martin Josefsson|titre=Characterizations of Orthodiagonal Quadrilaterals|périodique=Forum Geometricorum|volume=12|date=2012|lire en ligne=http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf|format=pdf|pages=13-25}}</ref> |
|||
: <math>R_1+R_3=R_2+R_4.</math> |
|||
Un corollaire intéressant est que les centres des cercles inscrits des quatres triangles diagonaux sont [[Points cocycliques|cocycliques]] si et seulement si le quadrilatère est circonscriptible. Ces quatres points forment alors dans ce cas un quadrilatère [[Quadrilatère inscriptible|inscriptible]] et [[Quadrilatère orthodiagonal|orthodiagonal]]<ref name=":0" />. Le même raisonnement s'applique aux centres des cercles exinscrits aux triangles extérieurs au côtés du quadrilatère évoqués précédemment. Ainsi un quadrilatère convexe est tangentiel si et seulement si les centres de ces quatre cercles exinscrits sont les sommets d'un [[quadrilatère inscriptible]]. |
|||
Un quadrilatère convexe ''ABCD'', dont les diagonales se coupent en ''P'', est tangentiel si et seulement si les quatre excentres des triangles ''APB'', ''BPC'', ''CPD'' et ''DPA'' opposés aux sommets ''B'' et ''D'' sont concycliques. Si ''R <sub>a</sub>'', ''R <sub>b</sub>'', ''R <sub>c</sub>'' et ''R <sub>d</sub>'' sont les exradii dans les triangles ''APB'', ''BPC'', ''CPD'' et ''DPA'' respectivement opposés aux sommets ''B'' et ''D'', alors une autre condition est que le quadrilatère est tangent si et seulement si |
|||
De plus, un quadrilatère convexe ''ABCD'' dont les diagonales se coupent en ''P'' est circonscriptible si et seulement si<ref name=":3" /> : |
|||
: <math>\frac{a}{\triangle(APB)}+\frac{c}{\triangle(CPD)}=\frac{b}{\triangle(BPC)}+\frac{d}{\triangle(DPA)}</math> |
|||
où ∆(''APB'' ) est l'aire du triangle ''APB'' . |
|||
Le point ''P'' coupe les diagonales en quatre segments. Si l'on note d'une part les longueurs ''AP'' = ''p''<sub>1</sub> et ''PC'' = ''p''<sub>2</sub>, et d'autre part ''BP'' = ''q''<sub>1</sub> et ''PD'' = ''q''<sub>2</sub>. Le quadrilatère sera circonscriptible si et seulement si l'une des égalités suivantes est vraie<ref>{{Article|langue=en|auteur1=Larry Hoehn|titre=A new formula concerning the diagonals and sides of a quadrilateral|périodique=Forum Geometricorum|volume=11|date=2011|lire en ligne=http://forumgeom.fau.edu/FG2011volume11/FG201122.pdf|format=pdf|pages=211-212}}</ref><ref name=":0" /> : |
|||
: <math>ap_2q_2 + cp_1q_1 = bp_1q_2 + dp_2q_1</math> |
|||
ou |
|||
: <math>\frac{(p_1+q_1-a)(p_2+q_2-c)}{(p_1+q_1+a)(p_2+q_2+c)}=\frac{(p_2+q_1-b)(p_1+q_2-d)}{(p_2+q_1+b)(p_1+q_2+d)}</math> |
|||
ou |
|||
: <math>\frac{(a+p_1-q_1)(c+p_2-q_2)}{(a-p_1+q_1)(c-p_2+q_2)}=\frac{(b+p_2-q_1)(d+p_1-q_2)}{(b-p_2+q_1)(d-p_1+q_2)}.</math> |
|||
== Caractérisations des quadrilatères circonscriptibles particuliers == |
|||
=== Losange === |
|||
Pour qu'un quadrilatère circonscriptible soit un [[losange]], il faut et suffit que ses angles opposés soient égaux<ref>{{Article|langue=en|prénom1=Michael|nom1=De Villiers|titre=95.14 Equiangular cyclic and equilateral circumscribed polygons|périodique=The Mathematical Gazette|volume=95|numéro=532|date=2011-03|issn=0025-5572|issn2=2056-6328|doi=10.1017/S0025557200002461|lire en ligne=https://www.cambridge.org/core/product/identifier/S0025557200002461/type/journal_article|consulté le=2023-01-03|pages=102–107}}</ref>. |
|||
=== Cerf-volant === |
|||
Pour qu'un quadrilatère circonscriptible soit un [[Cerf-volant (géométrie)|cerf-volant]], il faut et suffit que l'une des conditions suivantes soit vraie<ref name=":7" /> : |
|||
* L'aire est la moitié du produit des [[Diagonale|diagonales]] . |
|||
* Les diagonales sont [[Perpendicularité|perpendiculaires]] . |
|||
* Les deux cordes de tangences sont de même longueur |
|||
* Deux côtés opposées ont même longueurs tangentes associées. |
|||
* Les [[Quadrilatère|bimédianes]] sont de même longueur. |
|||
* Les produits des côtés opposés sont égaux. |
|||
* Le centre du cercle inscrit se trouve sur la diagonale, qui est l'axe de symétrie. |
|||
=== Quadrilatère bicentrique === |
|||
Si le cercle inscrit est tangent aux côtés ''AB'', ''BC'', ''CD'', ''DA'' en ''W'', ''X'', ''Y'', ''Z'' respectivement, alors un quadrilatère circonscriptible ''ABCD'' est [[Quadrilatère bicentrique|bicentrique]] si et seulement si l'une des conditions suivantes est vérifiée<ref name=":1" /><ref name=":8" /> : |
|||
[[Fichier:Bicentric quadrilateral.svg|vignette|Un quadrilatère bicentrique ''ABCD'' : les cordes de tangences sont perpendiculaire]] |
|||
* <math>AW\cdot CY=BW\cdot DY</math> |
|||
* <math>\frac{AC}{BD}=\frac{AW+CY}{BX+DZ}</math> |
|||
Comme on l'a vu plus haut, un quadrilatère est bicentrique si et seulement si les cordes de tangences sont perpendiculaires, c'est-à-dire si ''WY'' et perpendiculaire à ''XZ. L''e quadrilatère de contact d'un quadrilatère bicentrique est donc [[Quadrilatère orthodiagonal|orthodiagonal]]. |
|||
Un quadrilatère circonscriptible est bicentrique si et seulement si le rayon de son cercle inscrit [[Majorant|majore]] les rayons de tout autre quadrilatères tangentiels ayant même longueurs de côtés<ref>{{Article|auteur1=Albrecht Hess|titre=On a circle containing the incenters of tangential quadrilaterals|périodique=Forum Geometricorum|volume=14|date=2014|lire en ligne=http://forumgeom.fau.edu/FG2014volume14/FG201437.pdf|format=pdf|pages=389-396}}</ref>. |
|||
=== Trapèze === |
|||
Soient ''W'' et ''Y'' les points de tangence aux côtés ''AB'' et ''CD'' d'un quadrilatère circonscriptible ''ABCD''. Le quadrilatère est un [[trapèze]] de côtés parallèles ''AB'' et ''CD'' si et seulement si<ref>{{Article|langue=en|auteur1=Martin Josefsson|titre=The diagonal point triangle revisited|périodique=Forum Gometricorum|volume=14|date=2014|lire en ligne=http://forumgeom.fau.edu/FG2014volume14/FG201435.pdf|format=pdf|pages=381-385}}</ref> |
|||
: <math>AW\cdot DY=BW\cdot CY</math> |
|||
et ''AD'' et ''BC'' sont les côtés parallèles d'un trapèze si et seulement si |
|||
: <math>AW\cdot BW=CY\cdot DY.</math> |
|||
== Voir aussi == |
|||
* [[Cercle circonscrit]] |
|||
* [[Cercle inscrit]] |
|||
* [[Polygone circonscriptible]] |
|||
== Références == |
|||
<references /> |
|||
[[Catégorie:Pages avec des traductions non relues]] |
|||
Version du 3 janvier 2023 à 08:27

En géométrie euclidienne, un quadrilatère circonscriptible (ou quadrilatère tangentiel) est un quadrilatère convexe pour lequel il existe un cercle inscrit, c'est-à-dire un cercle situé à l'intérieur du quadrilatère et tangent à chacun de ses quatre côtés[1][2][3][4]. On dit alors que le quadrilatère circonscrit son cercle inscrit. Un quadrilatère circonscriptible est un cas particulier de polygone circonscriptible.
Si tout triangle est circonscriptible, ce n'est pas toujours vrai pour un quadrilatère. Par exemple, un rectangle n'est circonscriptible que si c'est un carré ; un rectangle ayant des côtés consécutifs de longueurs différentes n'est pas circonscriptible. Des conditions nécessaires et suffisantes pour qu'un quadrilatère soit circonscriptible sont détaillées ci-dessous.
Exemples
Les cerf-volants (y compris les losanges et les carrés) sont des quadrilatères circonscriptibles. Les cerf-volants sont d'ailleurs les quadrilatères qui sont à la fois orthodiagonaux et circonscriptibles[5].
Les trapèzes peuvent être également circonscriptibles.
Un quadrilatère peut être à la fois circonscriptible et inscriptible, c'est à dire que ses quatre sommets appartiennent à un même cercle, le cercle circonscrit. Un tel quadrilatère est dit bicentrique et a donc à la fois un cercle inscrit et un cercle circonscrit. Par exemple, les cerfs-volants droits (ayant deux angles droits opposés) et les trapèzes circonscriptibles isocèles sont bicentriques.
Caractérisations par les longueurs
Dans un quadrilatère circonscriptible, les quatre bissectrices des angles sont concourantes au centre du cercle inscrit. Réciproquement, un quadrilatère convexe dans lequel les quatre bissectrices sont concourantes est circonscriptible et leur point d'intersection est le centre du cercle inscrit[6].
D'après le théorème de Pitot, les sommes des longueurs des côtés deux à deux opposés sont égales entre elles, et égales au demi-périmètre s du quadrilatère. En notant a, b, c et d les longueurs successives des côtés, on a :
Réciproquement, tout quadrilatère convexe vérifiant a + c = b + d est nécessairement circonscriptible[3][6].
Si les côtés opposés d'un quadrilatère convexe ABCD (qui n'est pas un trapèze) se coupent en E et F, alors il est tangentiel si et seulement si au moins l'une des deux équations suivantes est vraie[6] :
ou
Cette dernière équation est proche de l'une des équations du théorème d'Urquhart, à ceci près que dans ce dernier l'équation relie les sommes des longueurs et non leur différence.
Un quadrilatère convexe ABCD est circonscriptible si et seulement si les cercles inscrits dans les deux triangles ABC et ADC sont tangents l'un à l'autre[3].
Une caractérisation par les angles entre la diagonale BD et les quatre côtés d'un quadrilatère ABCD, affirme qu'un quadrilatère est circonscriptible si et seulement si les angles vérifient[7] :

De plus, un quadrilatère convexe de côtés de longueurs a, b, c, d est circonscriptible si et seulement si
où Ra, Rb, Rc, Rd sont les rayons des cercles extérieurs tangents au côté de longueurs respectives a, b, c, d et aux prolongements des deux côtés adjacents[8].
Points de contacts et cordes de tangence
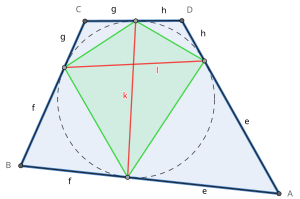
Le cercle inscrit est tangent aux quatre côtés en quatre points de contact. Le quadrilatère formé par ces quatre points est appelé quadrilatère de contact.
Dans un quadrilatère circonscriptible, les longueurs des segments reliant un sommet aux points de contact entre les côtés et le cercle inscrit sont appelées longueurs tangentes (notées e, f, g, h dans la figure de droite). Les deux longueurs tangentes issues d'un même sommet sont égales.
Les deux cordes de tangence (notées k et l sur la figure) sont les segments qui relient les points de contact des côtés opposés. Ce sont aussi les diagonales du quadrilatère de contact .
Aire
Formules non trigonométriques
L'aire S d'un quadrilatère circonscriptible est donnée par
où s est le demi-périmètre et r est le rayon du cercle inscrit . Une autre formule est[9]
où l'aire est exprimée en fonction des longueurs des diagonales p, q et des côtés a, b, c, d du quadrilatère.
L'aire d'un peut également être calculée à partir des quatre longueurs tangentes e, f, g, h ; le quadrilatère a alors pour aire[5] :
Il existe également une formule d'aire faisant intervenir à la fois les longueurs des côtés a, b, c, d et les longueurs tangentes e, f, g, h [5] :
Or, on a eg = fh si et seulement si le quadrilatère circonscriptible est également inscriptible. On en conclut que, à longueurs de côtés données, un quadrilatère circonscriptible d'aire maximale est bicentrique[10], et son aire est égale à .
Formules trigonométriques
Une formule trigonométrique donne l'aire en fonction des longueurs des côtés a, b, c, d et d'une paire d'angles opposés[9][11] :
où est l'angle des côtés au point A, est l'angle en B, etc.
On retrouve le résultat précédent concernant le quadrilatère circonscriptible d'aire maximale qui est également inscriptible puisque le sinus vaut 1 si les angles opposés sont supplémentaires .
Il existe une autre formule pour l'aire d'un quadrilatère circonscriptible ABCD faisant intervenir deux angles opposés et les distances entre les sommets et le centre I du cercle inscrit[11]
L'aire peut alors s'écrire en fonction de deux côtés adjacents et deux angles opposés[9]:
Ou encore, en fonction des longueurs des côtés et de l'angle θ entre les diagonales
Cette formule n'est valable que si les diagonales ne forment pas un angle droit (sans quoi la tangente n'est pas définie)
Inégalités
Comme vu plus haut, l'aire d'un quadrilatère circonscriptible de côtés a, b, c, d vérifie
l'égalité étant valable si et seulement si c'est un quadrilatère bicentrique.
Le demi-périmètre s du quadrilatère vérifie quant à lui
où r est le rayon du cercle inscrit. Il y a égalité si et seulement si le quadrilatère est un carré. Puisqu'on a S = rs on a l'inégalité
où l'égalité est vraie si et seulement si le quadrilatère est un carré.
Propriétés de partitions

Les quatre segments entre le centre du cercle inscrit et les points de tangence divisent le quadrilatère en quatre cerfs-volants droits.
Si une droite coupe un quadrilatère circonscriptible en deux polygones d' aires égales et de périmètres égaux, alors cette droite passe par le centre du cercle inscrit[6].
Rayon du cercle inscrit
Le rayon r du cercle inscrit dans un quadrilatère circonscriptible de côtés a, b, c, d est donné par[9] :
où S est l'aire du quadrilatère et s son demi-périmètre. Le rayon r est également maximal (à longueur de côtés donnés) si et seulement si le quadrilatère est bicentrique.
Le rayon du cercle inscrit peut également s'écrire en fonction des longueurs tangentes e, f, g, h définies plus haut[12]
On dispose également d'une expression du rayon en fonction des distances entre le centre du cercle I et les sommets du quadrilatère circonscriptible ABCD . En posant u = AI, v = BI, x = CI et y = DI, on a alors
où [13].
Si les cercles inscrits dans les triangles ABC, BCD, CDA, DAB ont des rayons respectivement, alors le rayon du cercle inscrit au quadrilatère circonscriptible ABCD est donné par
où . [14]
Formules d'angles
Les angles au sommets A,B,C,D d'un quadrilatère circonscriptible peuvent également s'écrire en fonction des longueurs tangentes e,f,g,h[5]
L'angle φ entre les cordes de tangence k et l est donné par
Diagonales
Les longueurs des diagonales p = AC et q = BD ont également une expression en fonction des longueurs tangentes e,f,g et h associées aux sommets A,B,C et D du quadrilatère circonscriptible[10]
Cordes de tangence
Si e, f, g et h sont les longueurs tangentes d'un quadrilatère circonscriptible, alors les longueurs des cordes de tangence sont[5]
où la corde de tangence de longueur k relie les côtés de longueurs a = e + f et c = g + h, et celle de longueur l relie les côtés de longueurs b = f + g et d = h + e.
Le rapport des carrés des longueurs des cordes de tangence est égal au rapport des côtés opposés correspondants[5].
Les deux cordes de tangence
- sont perpendiculaires si et seulement si le quadrilatère circonscriptible a aussi un cercle circonscrit (c'est à dire s'il est bicentrique)[5].
- ont des longueurs égales si et seulement si le quadrilatère est un cerf-volant[15].
La corde de tangence entre les côtés AB et CD dans un quadrilatère circonscriptible ABCD est plus longue que celle entre les côtés BC et DA si et seulement si la bimédiane entre les côtés AB et CD est plus courte que celle entre les côtés BC et DA[16].
Si le quadrilatère circonscriptible ABCD a pour points de tangence W sur AB et Y sur CD, et si la corde de tangence WY coupe la diagonale BD en M, alors le rapport des longueurs des tangentes est égal au rapport des segments de diagonale BD[17].
Alignement de points
Soient M1 et M2 respectivement les milieux des diagonales AC et BD d'un quadrilatère circonscriptible ABCD, I, et si les paires de côtés opposés se rencontrent en J et K avec M 3 étant le milieu de JK, alors les points M 3, M 1, I et M 2 sont colinéaires[6]. La droite qui les contient est la droite de Newton du quadrilatère.
Soient J et K les points d'intersection des prolongements des côtés opposés du quadrilatère circonscriptible ; et L et M les prolongements des côtés opposés de son quadrilatère de contact. Alors les quatre points J, L, K et M sont alignés[18].
Soient T1, T2, T3, T4 les points de tangence respectifs entre le cercle inscrit et les côtés AB, BC, CD et DA ; et soient N1, N2, N3, N4 leurs conjugués isotomiques respectifs par rapport aux côtés correspondants (c'est à dire que N1 est le point du segment AB tel que AT1 =N1B et ainsi de suite). On définit alors le point de Nagel du quadrilatère comme l'intersection des segments N1 N3 et N2 N4.Ces deux lignes coupent le périmètre du quadrilatère en deux parties égales. Le point de Nagel N, le centre de gravité G et le centre du cercle inscrit I sont alignés dans cet ordre, et on a de plus NG = 2 GI. Cette droite s'appelle la droite de Nagel du quadrilatère[19].

Soit quadrilatère ABCD circonscriptible dont le cercle inscrit a pour centre centre I et dont les diagonales se coupent en P, soient H1, H2, H3, H4 les orthocentres des triangles AIB, BIC, CID, DIA . Alors les points P, H1, H2, H3, H4 sont alignés[11].
Lignes concourantes et perpendiculaires
Les deux diagonales et les deux cordes de tangence sont concourantes[11]. On peut le démontrer à l'aide du théorème de Brianchon, à savoir qu'un hexagone dont tous les côtés sont tangents à une même conique a trois diagonales reliant les côtés opposés concourantes. À partir du quadrilatère, on forme un hexagone ayant deux angles plats en créant deux nouveaux sommets en deux points de tangence opposés ; les six côtés de cet hexagone sont tangents au cercle inscrit, de sorte que ses diagonales sont concourantes. Deux de ces diagonales sont les diagonales du quadrilatère, et la troisième diagonale de l'hexagone passe par les deux points de tangence opposés, ce qui prouve que la corde de tangence et les deux diagonales sont concourantes. On procède de même avec les deux autres point de tangence, ce qui prouve le théorème pour les quatre droites.
Si les prolongements des côtés opposés d'un quadrilatère circonscriptible se coupent en J et K, et les diagonales se coupent en P, alors JK est perpendiculaire au prolongement de IP où I est le centre du cercle inscrit[18].
Centre du cercle inscrit
Le centre du cercle inscrit au quadrilatère circonscriptible se trouve sur sa droite de Newton (passant par les milieux des diagonales)[20].
Le rapport de deux côtés opposés dans un quadrilatère circonscriptible peut être exprimé en termes de distances entre le centre I et les sommets[11]
Le produit de deux côtés adjacents dans un quadrilatère circonscriptible ABCD de centre I vérifie[21]
Si I est le centre du cercle inscrit à un quadrilatère ABCD, alors on a[11] :
De plus, le centre du cercle inscrit I dans un quadrilatère ABCD est confondu avec le barycentre du quadrilatère si et seulement si
Si I est le centre du cercle inscrit à un quadrilatère ABCD et Mp et Mq sont respectivement les milieux des diagonales AC et BD, alors :
où e, f, g et h sont les longueurs tangentes respectives associées à A, B, C et D. Par corollaire, le centre I se confond avec le barycentre si et seulement si I est le milieu du segment reliant les deux milieux des diagonales.
Si un mécanisme à quatre barres a forme d'un quadrilatère circonscriptible, il restera circonscriptible quel que soit la déformation du mécanisme, tant que le quadrilatère reste convexe[22]. Par exemple, si un carré est déformé en losange, il restera toujours circonscriptible, mais à un cercle inscrit plus petit. Si un côté est maintenu fixe alors que les autres sommets sont déplacés, le centre du cercle cercle inscrit décrit un cercle de rayon où a,b,c,d sont les côtés et s est le demi-périmètre.
Caractérisations par les quatre triangles diagonaux

Soit P l'intersection des diagonales dans un quadrilatère convexe ABCD. Les quatre triangles APB, BPC, CPD, DPA formés par côtés du quadrilatères et les diagonales, et forment une partition du quadrilatère en quatre.
Si r1, r 2, r3 et r4 les rayons des cercles inscrits à ces quatre triangles, le quadrilatère est circonscriptible si et seulement si[23]
De même, soient h1, h2, h3 et h4 les hauteurs respectives des quatre triangles cités précédemment issues de leur sommet commun (l'intersection des diagonales); le quadrilatère est tangentiel si et seulement si[7]
On a également avec les les rayons des cercles exinscrits aux quatre triangles diagonaux ra, rb, rc et rd dans les quatre mêmes triangles (les cercles étant tangents à un côté du quadrilatère et au prolongement des diagonales.). Le quadrilatère est circonscriptible si et seulement si[3] :
Enfin si R1, R2, R3 et R4 sont respectivement les rayons dans les cercles circonscrits aux triangles APB, BPC, CPD et DPA, alors le quadrilatère ABCD est circonscriptible si et seulement si[24]
Un corollaire intéressant est que les centres des cercles inscrits des quatres triangles diagonaux sont cocycliques si et seulement si le quadrilatère est circonscriptible. Ces quatres points forment alors dans ce cas un quadrilatère inscriptible et orthodiagonal[3]. Le même raisonnement s'applique aux centres des cercles exinscrits aux triangles extérieurs au côtés du quadrilatère évoqués précédemment. Ainsi un quadrilatère convexe est tangentiel si et seulement si les centres de ces quatre cercles exinscrits sont les sommets d'un quadrilatère inscriptible.
Un quadrilatère convexe ABCD, dont les diagonales se coupent en P, est tangentiel si et seulement si les quatre excentres des triangles APB, BPC, CPD et DPA opposés aux sommets B et D sont concycliques. Si R a, R b, R c et R d sont les exradii dans les triangles APB, BPC, CPD et DPA respectivement opposés aux sommets B et D, alors une autre condition est que le quadrilatère est tangent si et seulement si
De plus, un quadrilatère convexe ABCD dont les diagonales se coupent en P est circonscriptible si et seulement si[7] :
où ∆(APB ) est l'aire du triangle APB .
Le point P coupe les diagonales en quatre segments. Si l'on note d'une part les longueurs AP = p1 et PC = p2, et d'autre part BP = q1 et PD = q2. Le quadrilatère sera circonscriptible si et seulement si l'une des égalités suivantes est vraie[25][3] :
ou
ou
Caractérisations des quadrilatères circonscriptibles particuliers
Losange
Pour qu'un quadrilatère circonscriptible soit un losange, il faut et suffit que ses angles opposés soient égaux[26].
Cerf-volant
Pour qu'un quadrilatère circonscriptible soit un cerf-volant, il faut et suffit que l'une des conditions suivantes soit vraie[15] :
- L'aire est la moitié du produit des diagonales .
- Les diagonales sont perpendiculaires .
- Les deux cordes de tangences sont de même longueur
- Deux côtés opposées ont même longueurs tangentes associées.
- Les bimédianes sont de même longueur.
- Les produits des côtés opposés sont égaux.
- Le centre du cercle inscrit se trouve sur la diagonale, qui est l'axe de symétrie.
Quadrilatère bicentrique
Si le cercle inscrit est tangent aux côtés AB, BC, CD, DA en W, X, Y, Z respectivement, alors un quadrilatère circonscriptible ABCD est bicentrique si et seulement si l'une des conditions suivantes est vérifiée[5][18] :

Comme on l'a vu plus haut, un quadrilatère est bicentrique si et seulement si les cordes de tangences sont perpendiculaires, c'est-à-dire si WY et perpendiculaire à XZ. Le quadrilatère de contact d'un quadrilatère bicentrique est donc orthodiagonal.
Un quadrilatère circonscriptible est bicentrique si et seulement si le rayon de son cercle inscrit majore les rayons de tout autre quadrilatères tangentiels ayant même longueurs de côtés[27].
Trapèze
Soient W et Y les points de tangence aux côtés AB et CD d'un quadrilatère circonscriptible ABCD. Le quadrilatère est un trapèze de côtés parallèles AB et CD si et seulement si[28]
et AD et BC sont les côtés parallèles d'un trapèze si et seulement si
Voir aussi
Références
- G.-H. Nievengloski, « Sur le quadrilatère circonscriptible, et sur l’égalité des polygones », Nouvelles annales de mathématiques, 1re série, vol. 11, , p. 462-463 (lire en ligne [PDF])
- Patrice Debart, « Les quadrilatères au collège », sur debart.pagesperso-orange.fr (consulté le )
- (en) Martin Josefsson, « More Characterizations of Tangential Quadrilaterals », Forum Geometricorum, vol. 11, , p. 65-82 (lire en ligne [PDF])
- (en) Eric W. Weisstein, « Tangential Quadrilateral », sur mathworld.wolfram.com (consulté le )
- (en) Martin Josefsson, « Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral », Forum Geometricorum, vol. 10, , p. 119-130 (lire en ligne [PDF])
- Bogdan Enescu, Mathematical olympiad treasures, Birkhäuser, (ISBN 978-0-8176-8253-8, 0-8176-8253-8 et 978-0-8176-8252-1, OCLC 757539145, lire en ligne), p. 64-68
- (en) Nicusor Minculete, « Characterizations of a Tangential Quadrilateral, », Forum Geometricorum, vol. 9, , p. 113-118 (lire en ligne [PDF])
- (en) Martin Josefsson, « Similar Metric Characterizations of Tangential and Extangential Quadrilaterals », Forum Geometricorum, vol. 12, , p. 63-77 (lire en ligne [PDF])
- A. Robson et C. Durell, Advanced trigonometry, Dover Publications, (ISBN 0-486-43229-7 et 978-0-486-43229-8, OCLC 52509659, lire en ligne), p. 28-30
- Mowaffaq Hajja, « A condition for a circumscriptible quadrilateral to be cyclic », Forum Geometricorum, vol. 8, , p. 103-106 (lire en ligne [PDF])
- (en) Darij Grinberg, « Circumscribed quadrilaterals revisited » [PDF]
- (en) John P. Hoyt, « Quickies Q694 », Mathematics Magazine, vol. 57, no 4, , p. 239
- Martin Josefsson, « On the inradius of a tangential quadrilateral », Forum Geometricorum, vol. 10, , p. 27-34 (lire en ligne)
- Bogomolny, Alexander (2016), An Inradii Relation in Inscriptible Quadrilateral, Cut-the-knot, .
- (en) Martin Josefsson, « When is a Tangential Quadrilateral a Kite? », Forum Geometricorum, vol. 11, , p. 165-174 (lire en ligne [PDF])
- (en) Martin Josefsson, « The Area of a Bicentric Quadrilateral », Forum Geometricorum, vol. 11, , p. 155-165 (lire en ligne [PDF])
- Antonio Gutierrez, « Circumscribed Quadrilateral, Diagonal, Chord, Proportion. », sur gogeometry.com (consulté le )
- (en) Martin Josefsson, « Characterizations of Bicentric Quadrilaterals », Forum Geometricorum, vol. 10, , p. 165-173 (lire en ligne [PDF])
- Alexei Myakishev, « On Two Remarkable Lines Related to a Quadrilateral », Forum Geometricorum, vol. 6, , p. 289-295 (lire en ligne [PDF])
- (en) Nikolaos Dergiades et Dimitris M. Christodoulou,, « The two incenters of an arbitrary convex quadrilateral », Forum Geometricorum, vol. 17, , p. 245-254 (lire en ligne [PDF])
- Zuming Feng, 103 trigonometry problems : from the training of the USA IMO team, Birkhäuser, (ISBN 0-8176-4334-6, 978-0-8176-4334-8 et 978-0-8176-4432-1, OCLC 288195598, lire en ligne), p. 176-177
- Helen Barton, « Discussions: On a Circle Attached to a Collapsible Four-Bar », The American Mathematical Monthly, vol. 33, no 9, , p. 462–465 (ISSN 0002-9890, DOI 10.2307/2299611, lire en ligne, consulté le )
- Wu Wei Chao et Plamen Simeonov, « When Quadrilaterals Have Inscribed Circles: 10698 », The American Mathematical Monthly, vol. 107, no 7, , p. 657–658 (ISSN 0002-9890, DOI 10.2307/2589133, lire en ligne, consulté le )
- (en) Martin Josefsson, « Characterizations of Orthodiagonal Quadrilaterals », Forum Geometricorum, vol. 12, , p. 13-25 (lire en ligne [PDF])
- (en) Larry Hoehn, « A new formula concerning the diagonals and sides of a quadrilateral », Forum Geometricorum, vol. 11, , p. 211-212 (lire en ligne [PDF])
- (en) Michael De Villiers, « 95.14 Equiangular cyclic and equilateral circumscribed polygons », The Mathematical Gazette, vol. 95, no 532, , p. 102–107 (ISSN 0025-5572 et 2056-6328, DOI 10.1017/S0025557200002461, lire en ligne, consulté le )
- Albrecht Hess, « On a circle containing the incenters of tangential quadrilaterals », Forum Geometricorum, vol. 14, , p. 389-396 (lire en ligne [PDF])
- (en) Martin Josefsson, « The diagonal point triangle revisited », Forum Gometricorum, vol. 14, , p. 381-385 (lire en ligne [PDF])
























































