Théorème de Cantor-Bernstein

Pour les articles homonymes, voir Théorème de Bernstein.

Le théorème de Cantor-Bernstein, également appelé théorème de Cantor-Schröder-Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l'honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst Schröder. Cantor en donna une première démonstration, mais qui utilisait implicitement l'axiome du choix. Bernstein et Schröder en donnèrent des démonstrations qui ne dépendaient pas de cet axiome.

Historique

Georg Cantor l'énonce dans son livre Sur les fondements de la théorie des ensembles transfinis (1895-1897) mais ne le démontre pas. Felix Bernstein, élève de celui-ci en esquisse une démonstration dès 1896 à l'âge de 18 ans. Elle est publiée en 1898 sur proposition de Cantor dans Leçons sur la théorie des fonctions sous la plume d'Émile Borel. Ernst Schröder le démontre également dans un article daté de la même année, cette démonstration étant cependant considérée comme imparfaite.

Richard Dedekind en fit lui-même une démonstration en 1897 mais qui ne fut publiée qu'en 1930. Ernst Zermelo en fait une autre en 1906 qui reprend en fait les idées de Dedekind.

Énoncé

S'il existe une injection $f$ d'un ensemble $E$ vers un ensemble $F$, et une injection $g$ de l'ensemble $F$ vers l'ensemble $E$, alors il existe une bijection $h$ de $E$ sur $F$.

$\left\{\begin{matrix}\exist f \in F^E \;{\rm injective} \\ \exist g \in E^F \;{\rm injective} \end{matrix} \right. \Rightarrow \exist h \in F^E \;{\rm bijective}$

Démonstration n°1

Lemme préliminaire

Commençons par montrer que si $u$ est une application injective d'un ensemble $A$ vers une de ses parties, $B$, alors il existe une bijection $v$ de $A$ sur $B$.

Soit $(C_n)_{n \in \mathbb N}$ la suite définie par :

$\left\{\begin{matrix} C_0 = A\setminus B \\ \forall n \in \mathbb{N}^*, C_n = u( C_{n-1} ) \end{matrix} \right.$

Soit $C$ la réunion de tous les ensembles $(C_n)_{n \in \mathbb N}$ : $C=\bigcup_{n \in \mathbb N}C_n$

Soit alors $v$ l'application de $A$ dans $B$ définie par :

$\begin{matrix}v: & x \in C & \mapsto & u(x)\\ & x \notin C& \mapsto & x \end{matrix}$

$v$ est bien définie à valeurs dans $B$, car $u$ est à valeur dans $B$, et si $x \notin C$ alors $x \notin C_0$ et donc $x \in B$.

$v$ envoie injectivement $C$ dans $u(C)=\cup_{n\in\N}u(C_n)=\cup_{m\in\N^*}C_m\subset C$ et le complémentaire de C dans lui-même. C'est donc une injection.

Montrons que v est surjective. Soit $y \in B$. Montrons qu'il existe un $x \in A$ tel que $v(x)=y$.

• Si $y \in C$

alors il existe $i \in \mathbb{N}^*$ tel que $y \in C_i$. (i est strictement positif car $y \in B$, donc $y \notin C_0$).

Il existe donc $x \in C_{i-1} \subset C$ tel que $v(x)=u(x)=y$.

• Si $y \notin C$

alors $v(y)=y$

Donc $v$ est bijective. Ce qui démontre la première proposition.

Interprétation

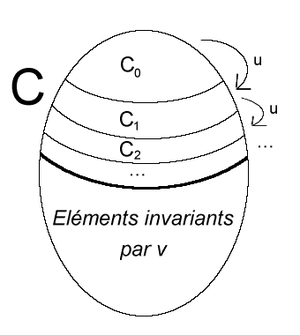
On peut donner une interprétation concrète du résultat montré ci-dessus. A est l'ensemble (infini) des spectateurs d'un théâtre (infini). Chaque spectateur a réservé une place, et initialement, on suppose que chaque place est occupée par un spectateur, mais pas forcément par le spectateur qui a réservé cette place. B est alors l'ensemble des spectateurs assis. Par ailleurs, les ensembles étant infinis, il peut rester des spectateurs debout. L'application u est l'application qui, à un spectateur x associe le spectateur y = u(x) assis à la place de x.

$C_0$ est l'ensemble des spectateurs initialement debout. Ces spectateurs se rendent à leur place et délogent leur occupant. Ceux-ci forment alors l'ensemble $C_1$. Ces derniers procèdent de même. $C_n$ désigne les spectateurs debout à la n-ème étape. Ils vont aux places qu'ils ont réservées et en chassent leurs occupants. On itère une infinité de fois. C désigne l'ensemble des spectateurs qui se sont levés au moins une fois (y compris ceux qui étaient debout initialement).

L'application v désigne l'application, qui, à un spectateur x qui doit se lever, associe le spectateur y qu'il va déloger, ou bien qui, à un spectateur x qui reste toujours assis, associe x lui-même. L'application réciproque de v est l'application, qui, à un spectateur y qui est dérangé, associe le spectateur x qui vient prendre sa place, ou bien qui, à un spectateur y jamais dérangé, associe y lui-même.

Démonstration finale du théorème

Montrons alors le théorème initial.

Soit B = g(F) l'image de F par l'injection g. L'application u = g o f est une injection de E dans B, avec $B \subset E$. Donc il existe une bijection v de E sur B. Comme g est une injection et g(F)=B, elle définit par restriction une bijection h de F sur B. La composée h^-1ov est une bijection de E sur F, ce qui démontre le théorème de Cantor-Bernstein.

Démonstration n°2

Un lemme préliminaire

Cette démonstration repose sur le lemme suivant, cas particulier du théorème de Knaster-Tarski. Soit $E$ un ensemble et $G : \mathfrak P(E) \to \mathfrak P(E)$ (où $\mathfrak P(E)$ est l'ensemble des parties de $E$) une application croissante, i.e. $A \subset B \Longrightarrow G(A) \subset G(B)$. Alors $G$ admet un point fixe, i.e. $\exists M, G(M) = M$.

En effet, posons $S = \{A \;|\; A \subset G(A)\}$ et $M = \cup_{A \in S} A$. Alors :

• pour tout $A \in S$, d'une part $A \subset G(A)$, d'autre part $A \subset M \Longrightarrow G(A) \subset G(M)$ car $G$ est croissante. Donc $M = \cup_{A \in S} A \subset \cup_{A \in S} G(A) \subset G(M)$ et donc $M \in S$. $M$ est donc la partie maximale de $S$

• $M \subset G(M)$ donc $G(M) \subset G(G(M))$ car $G$ est croissante. Donc $G(M) \in S$ donc $G(M) \subset M$ compte tenu de la maximalité de $M$ comme élément de $S$. On a donc bien $G(M) = M$

Démonstration finale

Soient maintenant $f$ injective de $E$ dans $F$ et $g$ injective de $F$ dans $E$. Pour toute partie $A$ de $E$, on pose $G(A) = E \setminus g(F \setminus f(A))$, c'est-à-dire que G(A) s'obtient en prenant l'ensemble f(A) des images par f des éléments de A, puis le complémentaire dans F de cet ensemble d'images par f, puis l'ensemble des images par g des éléments de ce complémentaire, et enfin le complémentaire dans E de cet ensemble d'images par g. Il n'est pas difficile de vérifier que $G$ est croissante.

On introduit alors la partie $M$ du lemme préliminaire. Cette partie est invariante par $G$ ce qui signifie que $g(F-f(M))$ est exactement le complémentaire de $M$ dans $E$.

On pose :

si $x \in M, h(x) = f(x)$

si $x \notin M, h(x) = g^{-1}(x)$

$h$ est bijective de $E$ dans $F$.

$M$ joue un rôle comparable à la partie $C$ dans la première démonstration ou à $E_p \cup E_{\infty}$ dans la démonstration qui suit.

Démonstration n° 3

Appelons ancêtres d'un élément $x$ de $E$ l'antécédent de $x$ par $g$ (s'il existe) puis l'antécédent de cet antécédent par $f$, etc. Procédons de même pour les éléments de $F$.

Notons $E_p$ (resp. $E_i$) l'ensemble des éléments de $E$ ayant un nombre pair (resp. impair) d'ancêtres. $E_p$ n'est autre que la partie $C$ de la première démonstration. Notons $E_\infty$ l'ensemble des éléments de $E$ ayant un nombre infini d'ancêtres. $E_p$, $E_i$ et $E_\infty$ forment une partition de $E$. Définissons de même $F_p$, $F_i$ et $F_\infty$.

$f$ est une bijection de $E_p$ sur $F_i$ et aussi de $E_\infty$ sur $F_\infty$. $g$ est une bijection de $F_p$ sur $E_i$, et sa réciproque est donc une bijection de $E_i$ sur $F_p$.

On peut ainsi construire une bijection de $E$ sur $F$.

Applications

Si l'on considère la technique naïve qu'a un enfant pour compter le nombre d'éléments d'un ensemble, cela revient quasiment toujours à associer chacun des éléments à un autre d'un ensemble connu dont le nombre d'éléments est connu.

Il peut s'agir soit d'associer chacun des éléments à compter avec l'un des doigts, soit d'associer chacun des éléments avec un nombre que l'on réciterait à haute voix (un, deux, trois, etc.), par exemple.

En clair, compter se fait naïvement en effectuant une bijection d'un ensemble dont la « dimension » est connue vers un autre dont la dimension est inconnue.

Ce théorème s'interprète alors comme disant : « Si je peux compter une partie d'un ensemble avec la totalité des éléments d'un autre ensemble, et réciproquement, alors ils ont le même nombre d'éléments ». Ce qui est évident pour des ensembles finis. Ce théorème généralise alors cette notion pour des ensembles infinis.

Si je peux compter un certain nombre de billes de mon sac de billes avec mes dix doigts, et qu'avec la totalité de mes billes, je peux les associer avec certains de mes doigts, alors j'ai exactement dix billes.

À partir de là, ce théorème représente l'une des briques de base pour généraliser la notion de tailles d'ensembles à des ensembles infinis.

Généralisation

Soient X un ensemble non vide et $\sim$ une relation d'équivalence sur l'ensemble des parties de X. On suppose qu'elle vérifie les deux propriétés:

• si $\ A \sim B$ alors il existe une bijection f de A dans B telle que, pour tout sous-ensemble C de A, $\ f(C) \sim C$;
• si $A_{1} \cap A_{2}=B_{1} \cap B_{2}=\emptyset$ et $\ A_{1} \sim B_{1}$ et $\ A_{2} \sim B_{2}$ alors $A_{1} \cup A_{2} \sim B_{1} \cup B_{2}$.

Soient deux ensembles A et B, un sous-ensemble $A_{1}$ de A et un sous-ensemble $B_{1}$ de B. On suppose que $\ A \sim B_{1}$ et $\ B \sim A_{1}$. Alors $\ A \sim B$.

Ceci peut également être démontré sans l'axiome du choix. Dans le cas particulier où $X=E \cup F$ et $\sim$ est la relation d'équipotence, on retrouve le résultat précédent.