Os d'Ishango

Les os d'Ishango, également appelés bâtons d'Ishango, sont des artéfacts archéologiques découverts au Congo et datés de peut-être 20 000 ans[1],[2],[3]. Selon certains auteurs, il pourrait s'agir de la plus ancienne attestation de la pratique de l'arithmétique dans l'histoire de l'humanité. Ils ont été, en premier lieu, considérés comme des bâtons de comptage. Puis, quelques scientifiques ont avancé l'idée qu'il s'agirait d'une compréhension bien plus avancée que le simple comptage. Cette thèse est rejetée par d'autres spécialistes.
Découverte[modifier | modifier le code]
Dans les années 1950, le géologue belge Jean de Heinzelin de Braucourt découvrit ces ossements dans des couches de cendres volcaniques au bord du lac Édouard dans la région d'Ishango au Congo belge (aujourd'hui République démocratique du Congo), près de la frontière ougandaise.
On estima d'abord qu'il s'agissait d'os datant de 9 000 à 6 500 ans avant notre ère, mais une datation du site où ils furent découverts porta leur création à quelque 20 000 ans.
Les ossements[4] ont été exposés au Muséum des sciences naturelles de Belgique à Bruxelles et sont présentés maintenant au Musée royal de l’Afrique centrale (MRAC) à Tervuren.
Caractéristiques principales[modifier | modifier le code]
Il s'agit de deux os d'approximativement 10 cm et 14 cm, provenant d'animaux non identifiés (on pense à des os humains, de singe ou de lion). Un fragment de quartz est enchâssé au sommet du plus petit. Ces os portent plusieurs incisions sur chacune de leurs faces.
Caractéristiques principales du premier os[modifier | modifier le code]
Cet os, le plus petit des deux, est le premier à avoir été exposé au muséum de Bruxelles.
Il porte plusieurs incisions, organisées en groupes de trois colonnes.
Colonne de gauche[modifier | modifier le code]

La colonne peut être divisée en quatre groupes. Chaque groupe possède respectivement 19, 17, 13 et 11 entailles.
Colonne centrale[modifier | modifier le code]

La colonne peut être divisée en huit groupes. Par un comptage approximatif et instinctif, on peut compter (entre parenthèses figure le nombre maximal d'encoches) : 7(8), 5(7), 5(9), 10, 8(14), 4(6), 6, 3 entailles.
Colonne de droite[modifier | modifier le code]

La colonne peut être divisée en quatre groupes. Chaque groupe possède respectivement 9, 19, 21 et 11 entailles.
Caractéristiques principales du second os[modifier | modifier le code]
Le second os est encore mal connu. On sait qu'il est composé de six groupes de 20, 6, 18, 6, 20 et 8 entailles.
Interprétations possibles[modifier | modifier le code]
Interprétations possibles du premier os[modifier | modifier le code]

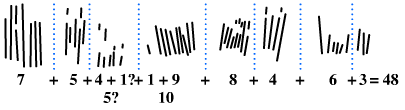

Quelques auteurs ont proposé des spéculations sur les entailles présentes sur l'os d'Ishango, en les interprétant comme une notation arithmétique[5].
Dans les années 1950, Jean de Heinzelin de Braucourt fut le premier à considérer cet os comme un vestige présentant un intérêt pour l'histoire des mathématiques. Il l'assimila à un jeu d'arithmétique et donna un ordre arbitraire aux différentes colonnes, soit la première (b), la seconde (c) et la troisième (a) en suivant les notations du schéma ci-dessous.
L'inventeur nota que la colonne (c) est compatible avec un système de numération de base 10, du fait que les entailles y sont groupées comme :
- 21 = 20 + 1
- 19 = 20 - 1
- 11 = 10 + 1
- 9 = 10 - 1.
Il reconnut également, en colonne (a), l'écriture dans l'ordre des nombres premiers compris entre 10 et 20, soit 11, 13, 17 et 19.
Enfin, la colonne (b) semble illustrer la méthode de duplication multiplication par 2 utilisée en une période plus proche de nous dans la multiplication égyptienne, soit 3 × 2 = 6, 4 × 2 = 8 et 5 × 2 = 10.
À la suite de ses observations, J. de Heinzelin admet de fait que les « paléo-mathématiciens » d'Ishango avaient la connaissance des nombres premiers. Plus que comme un jeu mathématique, l'os d'Ishango semble, selon lui, se présenter comme un document crypté faisant appel à l'arithmétique et fondé sur les nombres premiers et les duplications.
D'autres ont poursuivi les travaux de J. de Heinzelin, en particulier Dirk Huylebrouck[6] (faculté d'architecture, Université de Louvain) et Vladimir Pletser (Agence spatiale européenne). Écartant l'hypothèse des « nombres premiers », ils ont proposé d'autres extrapolations basées sur le même présupposé d'une notation arithmétique, contribuant ainsi à la notoriété actuelle des os d'Ishango[7].
Interprétations possibles du second os[modifier | modifier le code]
La série de nombres 20, 6, 18, 6, 20, 8 « ferait penser à » un calcul en bases 10, 12, 6 ou 60. Le second bâton d'Ishango « paraît donc confirmer » la thèse de comptage dans ces bases.
Réfutation des différentes thèses[modifier | modifier le code]
En 2010, Olivier Keller[8], dans une virulente analyse sur BibNum[9], critique les tentatives de surinterpréter les traces archéologiques en histoire des mathématiques[10]. Dès 1996, Steven Mithen[11] allait plus loin : en l'absence de critères stricts, on ne peut pas interpréter ces marques comme des symboles et encore moins une série de telles marques comme une « notation ».
Notes et références[modifier | modifier le code]
- Le Bâton d'Ishango... 23.000 ans... le plus vieil objet mathématique, [1], [2] et [3], Institut royal des sciences naturelles de Belgique.
- (en) Eric W. Weisstein, « Ishango Bone », sur MathWorld.
- Les os incisés d'Ishango font naître la numération en Afrique, Le Monde, 28 février 2007.
- Une telle découverte, bien que rare, n'était pas isolée, et d'autres fossiles pouvant être interprétés comme bâtons de comptage sont aujourd'hui connus, tels que par exemple l'os de Lebombo.
- La thèse du calendrier lunaire, défendue dans les années 1970 par le journaliste scientifique Alexander Marshack, est aujourd'hui généralement abandonnée.
- (en) « Start page D. Huylebrouck ».
- Cf. les nombreuses autoréférences de leur réponse à Keller 2010 ([11] est la suite A100000 de l'OEIS et [6] est en fait un abstract : pdf p. 4-5).
- Agrégé de mathématiques et auteur d'une thèse de doctorat dirigée par Jean Dhombres : Préhistoire de la géométrie : la gestation d'une science d'après les sources archéologiques et ethnographiques, soutenue en 1998 à l'EHESS, puis de plusieurs livres d'histoire des mathématiques.
- Site édité jusqu'à fin 2014 par le CERIMES.
- Olivier Keller, « Les fables d’Ishango, ou l’irrésistible tentation de la mathématique-fiction » », sur Bibnum, (cette analyse a fait l'objet, de la part de V. Pletser et D. Huylebrouck, d'une demande de réponse (juin 2016), qui figure à la suite de l'analyse ainsi que sur arXiv:1607.00860). Voir aussi O. Keller, « Préhistoire de la géométrie : le problème des sources », sur IREM de La Réunion, .
- (en) S. Mithen, « Notation, Paleolithic », dans Neil Asher Silberman, The Oxford Companion to Archaeology, vol. 1, OUP, , 2e éd. (1re éd. 1996) (lire en ligne), p. 555-557.
Liens externes[modifier | modifier le code]
- (en) « Light on Ishango », sur perso.fundp.ac.be (Philippe Lambin, professeur de physique à l'université de Namur) (consulté le ).

